Les tragédies grecques existaient aussi chez les mathématiciens de l’Antiquité. La découverte de la racine carrée du nombre 2 est le sujet de l’une d’entre elles, qui a trouvé une fin heureuse à l’époque moderne.

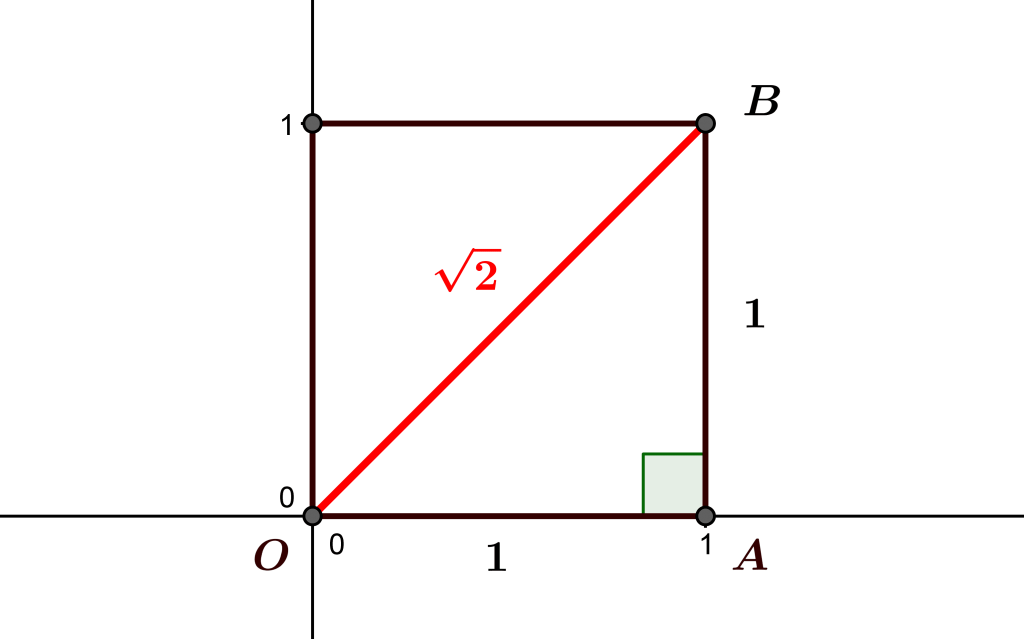
Un disciple de Pythagore « mesure » la diagonale du carré

La philosophie de l’école pythagoricienne voyait dans le nombre rationnel l’expression de l’harmonie de la nature et du cosmos, sur le modèle des rapports numériques simples qui exprimaient les intervalles fondamentaux en musique, découverts par Pythagore à partir des rapports de longueur du monocorde. Le mathématicien Hippase de Métaponte, disciple de l’école pythagoricienne, étudiait la « commensurabilité » (co-mesurabilité) des grandeurs géométriques. Il fut peut-être le premier à étudier la longueur de la diagonale d’un carré, en prenant le carré le plus simple, de côté \(1\).

Il établit que cette diagonale était incommensurable aux cathètes (côtés adjacents à l’angle droit, c’est-à-dire autres que l’hypoténuse dans un triangle rectangle) du demi-carré. Cela signifie qu’il n’existe aucune unité de mesure commune qui permette d’exprimer les longueurs des cathètes et la longueur de la diagonale comme multiples entiers de cette unité. En effet, par le théorème de Pythagore, dans le cas du carré de côté \(1\) l’aire du carré construit sur la diagonale est la somme des aires des carrés construits sur chaque côté, c’est-à-dire \(2\). La longueur de la diagonale doit donc être un nombre dont le carré vaut \(2\), et cette longueur ne peut donc pas être un nombre rationnel, ce qu’on savait déjà démontrer dans l’Antiquité.

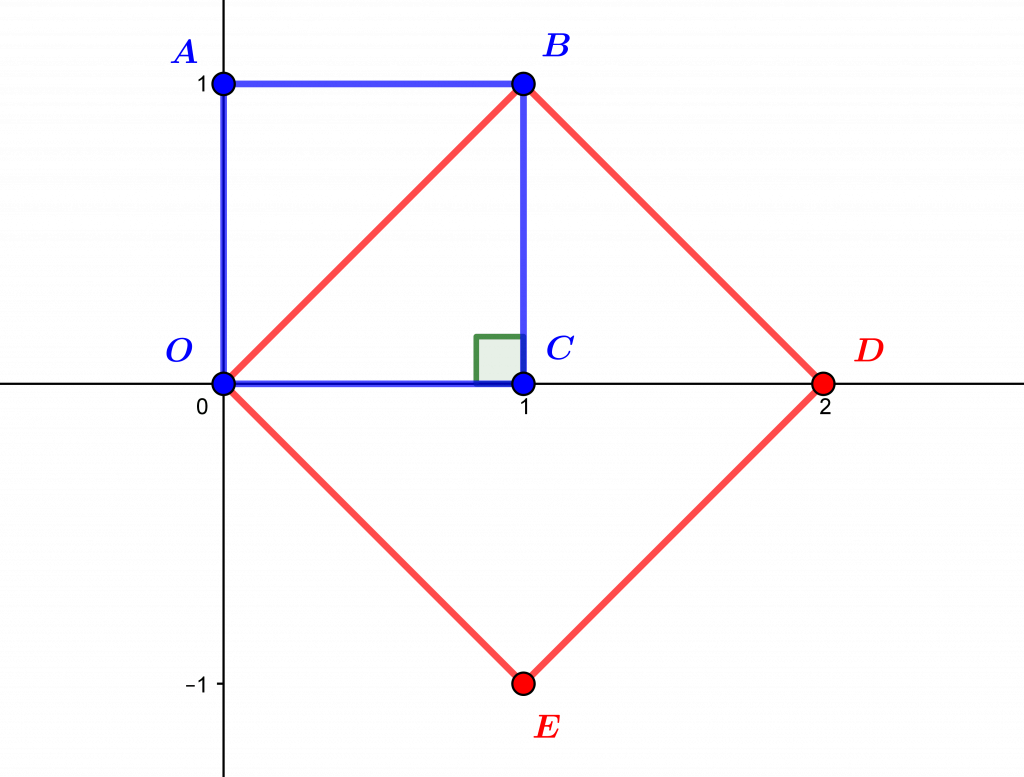
Le carré \(OBDE\) est construit sur la diagonale \([OB]\) du carré \(OABC\), laquelle est aussi l’hypoténuse du triangle rectangle (demi-carré) \(OBC\). Par le théorème de Pythagore, l’aire de \(OBDE\) est le double de l’aire de \(OABC\), soit \(2\).

Démontrer l’irrationalité de \(\sqrt 2\)

Selon certaines traditions, cette découverte d’Hippase, ou bien sa promulgation en-dehors du cercle des pythagoriciens, aurait précipité sa fin, les autres disciples l’ayant noyé lors d’un voyage en mer. Il est plutôt probable qu’il ait été exclu de l’école. Pour autant, sa découverte s’inscrivit dans le corpus mathématique de l’Antiquité grecque, puisqu’on y connaissait déjà une démonstration de l’irrationalité de \(\sqrt 2\), ou pour le dire dans le langage d’une civilisation qui ne connaissait pas les nombres réels : qu’il n’existe aucun nombre rationnel dont le carré vaut \(2\).

L’argument classique de cette démonstration se présente comme suit. Supposons par l’absurde qu’il existe un nombre rationnel \(r\) tel que \(r^2=2\), et écrivons-le sous la forme \(r=a/b\), avec \(a\) et \(b\) sans facteurs communs (c’est-à-dire « premiers entre eux« ). On obtient \(2=(a/b)^2=a^2/b^2\), soit \(a^2=2b^2\), si bien que \(a^2\) est pair (multiple de \(2\)). Puisque le produit de deux nombres impairs est impair, nous devons en conclure que \(a\) lui-même est pair, si bien que \(a=2c\) pour un entier \(c\). On en déduit que \(2b^2=a^2=(2c)^2=4c^2\), d’où \(b^2=2c^2\) en divisant les deux membres par \(2\), et par le même raisonnement, cette fois-ci que \(b\) est pair ! Mais ceci contredit l’hypothèse, à savoir que \(a\) et \(b\) n’ont aucun facteur commun. Par reductio ad absurdum, on en conclut qu’un tel nombre \(r\) n’existe pas.

Les nombres irrationnels

La question de la « réalité » des grandeurs non rationnelles, comme la racine carrée de \(2\), appelées aujourd’hui nombres « irrationnels », a longtemps occupé les mathématiciens jusqu’à la découverte ou la création des nombres réels, selon le point de vue adopté. Au sein des nombres irrationnels, il existe de plus une distinction entre les nombres dits algébriques et les nombres dits transcendants.

Un nombre algébrique est un nombre réel ou complexe qui est solution d’une équation en une variable et à coefficient dans l’ensemble \(\mathbb Q\) des nombres rationnels. Une telle équation est de la forme \(x^n+a_1x^{n-1}+a_2x^{n-2}+\ldots +a_{n-2}x^2+a_{n-1}x+a_n=0\), où \(a_1,\ldots,a_n\) sont des nombres rationnels. La racine carrée (positive) de \(2\), nombre réel noté \(\sqrt 2\), est donc un nombre algébrique puisqu’elle est solution de l’équation \(x^2-2=0\). L’autre solution de cette équation est le nombre \(-\sqrt 2\). Le nombre complexe \(i\) est un autre exemple, analogue, de nombre algébrique, solution de l’équation \(x^2+1=0\).

Un nombre transcendant est au contraire un nombre réel ou complexe qui n’est solution d’aucune équation de la forme précédente. Les nombres irrationnels transcendants les plus célèbres sont le nombre \(\pi\) (longueur du demi-cercle de rayon \(1\)) et le nombre \(e\) (base de la fonction exponentielle). Or, on peut démontrer que les points qu’on peut construire à l’aide de la règle et du compas ont toujours des coordonnées qui sont des nombres réels algébriques. Ainsi, l’usage du cercle dans ces constructions ne permet pas d’en représenter la circonférence comme une grandeur constructible.

Conclusion

La découverte de l’irrationalité de \(\sqrt 2\), ou de l’incommensurabilité de la diagonale du carré, a été une tragédie pour la philosophie pythagoricienne. Pourtant, cette découverte a engendré des siècles d’interrogation mathématique, pour aboutir à l’une des créations les plus emblématiques de la science, les nombres réels. Et ces nombres permettent de mesurer toutes les grandeurs réelles, et de sauvegarder l’essentiel de la philosophie pythagoricienne : tous les rapports de grandeurs, même des courbes aux lignes droites, peuvent être représentés par des nombres !

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :

Pour aller plus loin

La théorie élémentaire des nombres rationnels prolonge l’arithmétique naturelle des nombres entiers et prépare la théorie des nombres réels. Découvrez cette théorie et son rapport à l’irrationalité de \(\sqrt 2\) dans le cours numéro 3 du semestre I de MATHESIS :

Mathesis 1.3 : Arithmétique Elémentaire (Des nombres entiers naturels aux nombres rationnels)