On rencontre souvent en géométrie et en physique une expression trigonométrique du produit scalaire. A partir d’une définition du cosinus et du sinus d’un angle affine, on peut la démontrer directement grâce aux propriétés élémentaires du produit scalaire. On tire de cette expression la loi des cosinus ou théorème d’Al-Kashi, qui est une généralisation du théorème de Pythagore, exprimant les relations entres les carrés des longueurs d’un triangle quelconque, à l’aide du cosinus de l’un des angles.

1.Angles affines, cosinus et produit scalaire

1.1.Angles affines orientés

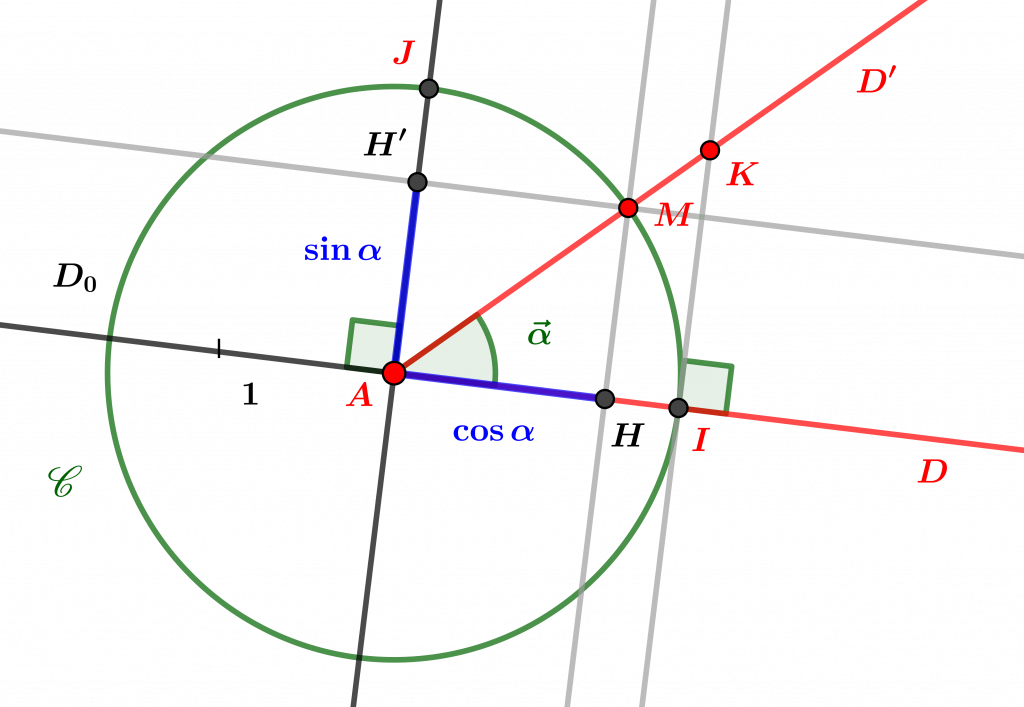
En rapportant, par une rotation et/ou une translation, un angle orienté à un point du cercle trigonométrique, on définit naturellement le sinus d’un tel angle comme l’ordonnée de ce point (voir Le cercle trigonométrique). Une approche alternative utile pour établir les relations trigonométriques fondamentales dans le triangle, consiste à travailler directement à partir d’une réalisation de l’angle orienté, c’est-à-dire d’un angle « affine ». Un tel angle $\vec\alpha$ correspond à la donnée d’un point $A$ appelé sommet de l’angle, et de deux demi-droites $D$ et $D’$ basées en $A$, et donc du triplet $\vec\alpha=(A,D,D’)$ : on prend en compte l’orientation de l’angle à travers l’ordre de $D$ et $D’$, de sorte que le triplet $(A,D’,D)$ définit un angle « opposé », c’est-à-dire orienté dans l’autre sens. Sur la figure suivante, traçons le cercle $\mathscr C$ de centre $A$ et de rayon $1$, qui coupe $D$ (première demi-droite de l’angle) en $I$, et $D’$ (deuxième demi-droite de l’angle) en $M$, et menons par le point $J$ du cercle $\mathscr C$ la perpendiculaire à $D$ passant par $A$, de sorte que $det(\vec{AI},\vec{AJ})>0$, c’est-à-dire que $(\vec{AI},\vec{AJ})$ soit une base (orthonormée) directe (voir L’orientation du plan euclidien) ; on dit que $(A,\vec{AI},\vec{AJ})$ est un repère orthonormé direct. Si $H$ est la projection orthogonale de $M$ sur $D$ et $H’$ la projection orthogonale de $M$ sur la droite $(AJ)$, alors par définition le cosinus de $\alpha$ est la mesure algébrique $\overline{AH}$ et le sinus de $\alpha$ est la mesure algébrique $\overline{AH’}$.

1.2.Expression trigonométrique du produit scalaire

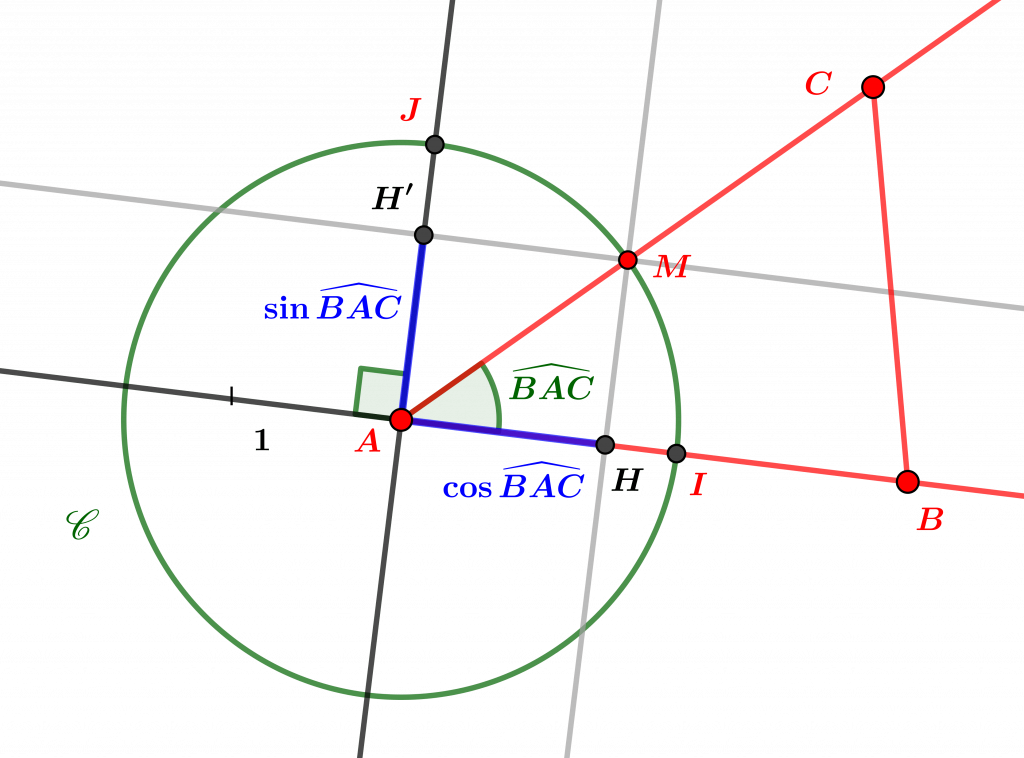
Rappelons que le produit scalaire de deux vecteurs plans $u=(a,b)$ et $v=(c,d)$ est un nombre réel défini de manière analytique (c’est-à-dire à l’aide de leurs coordonnées) par $u.v=ac+bd$. On rencontre une autre expression du produit scalaire, notamment dans des contextes faisant intervenir de la géométrie, comme en physique, et qui en fournit l’expression en fonction du cosinus de l’angle entre les vecteurs $u$ et $v$, sous la forme $u.v=||u||.||v||.\cos (u,v)$ (voir Le produit scalaire naturel). Nous allons ici établir cette relation à partir des angles affines orientés. Si $A,B,C$ sont trois points distincts du plan, convenons de noter $\widehat{BAC}$ l’angle affine orienté $(A,[AB),[AC))$ défini à la section précédente : c’est par définition l’angle des vecteurs $\vec{AB} $ et $\vec{AC}$, c’est-à-dire l’angle des vecteurs unitaires $(1/AB).\vec{AB}$ et $(1/AC).\vec{AC}$, si on les définit comme dans [Angles de vecteurs]. Avec les notations et définitions de la section précédente, on a $(1/AB).\vec{AB}=\vec{AI}$ et $(1/AC).\vec{AC}=\vec{AM}$, et le cosinus et le sinus de l’angle affine $\widehat{BAC}$ définis ici sont alors ceux de l’angle de vecteurs $(\vec{AI},\vec{AM})$ (voir la figure suivante). Par définition de $\cos \widehat{BAC}$ et $\sin \widehat{BAC}$, on peut alors décomposer le vecteur $\vec{AM}$ dans la base $(\vec{AI},\vec{AJ})$ sous la forme $$\vec{AM}=\cos\widehat{BAC}.\vec{AI}+\sin\widehat{BAC}.\vec{AJ},$$ et donc calculer le produit scalaire $\vec{AI}.\vec{AM}=\vec{AI}.(\cos\widehat{BAC}.\vec{AI}+\sin\widehat{BAC}\vec{AJ})=\cos\widehat{BAC}. AI^2+\sin\widehat{BAC}.(\vec{AI}.\vec{AJ}),$ par les propriétés du produit scalaire et parce que $\vec{AI}.\vec{AI}=AI^2$. Or, on a $AI^2=1$ par définition de $I$, et $\vec{AI}.\vec{AJ}=0$ puisque $\vec{AI}$ et $\vec{AJ}$ sont orthogonaux. On a donc simplement $$\vec{AI}.\vec{AM}=\cos\widehat{BAC}=\cos\widehat{IAM}.$$ On en déduit l’expression trigonométrique du produit scalaire, puisqu’on a $\vec{AB}=AB.\vec{AI}$ et $\vec{AC}=AC.\vec{AM}$, soit la

Proposition 1
Si $A,B,C$ sont trois points distincts du plan, alors on a $\vec{AB}.\vec{AC}=AB.AC.\cos\widehat{BAC}$.

2.Le théorème d’Al-Kashi et le produit scalaire

Ce point de vue « affine » sur le produit scalaire des vecteurs du plan trouve une application naturelle dans la géométrie du triangle, puisque la donnée d’un triangle $ABC$ est la même que celle de trois points $A,B,C$ distincts du plan.

2.1.Une généralisation du théorème de Pythagore

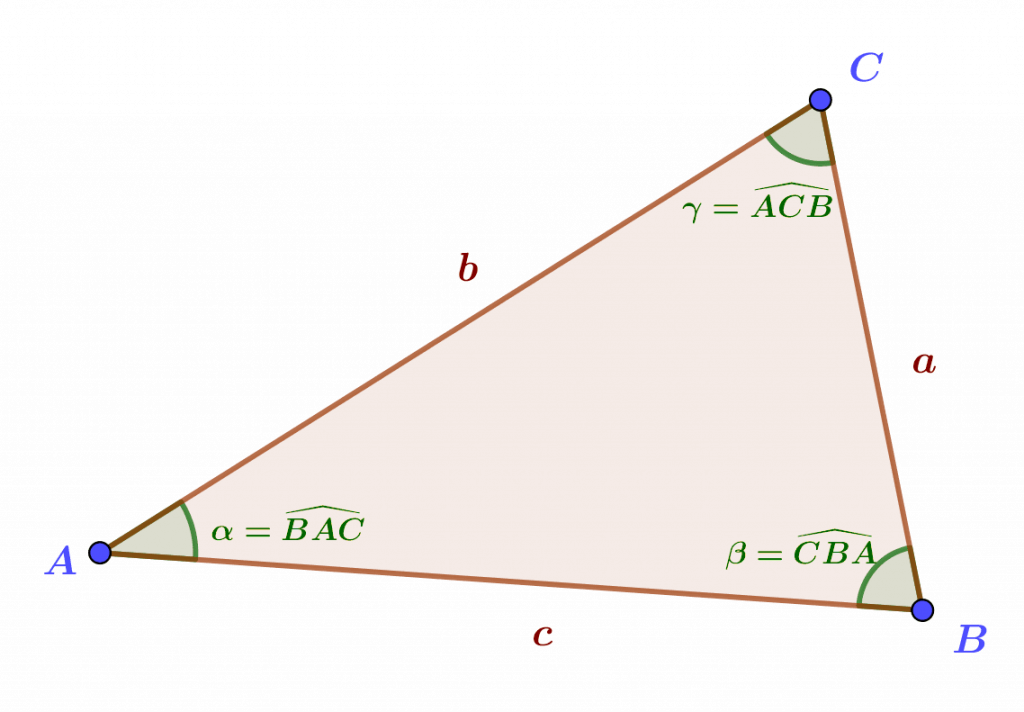
Le théorème de Pythagore établit une relation entre les longueurs de l’hypoténuse et celles des deux autres côtés (appelés « cathètes« ) d’un triangle rectangle. Dans le cas d’un triangle quelconque, l’expression trigonométrique du produit scalaire permet de généraliser assez directement le théorème de Pythagore pour exprimer les relations entre la longueur d’un côté quelconque et celle des deux autres, grâce au cosinus de l’angle opposé à ce côté. On obtient la relation appelée loi des cosinus, aussi connue sous le nom de « théorème d’Al-Kashi », mathématicien et astronome perse du 15ième siècle. Il s’agit en fait de trois relations, qui sont essentiellement identiques puisque le triangle est quelconque, et qu’on établit comme suit. On se donne un triangle $ABC$ et on calcule le carré de la longueur $BC$ comme la norme du vecteur $\vec{BC}$, c’est-à-dire comme son « carré scalaire » : on a $BC^2=\vec{BC}.\vec{BC}=(\vec{BA}+\vec{AC}).(\vec{BA}+\vec{AC})=\vec{BA}.\vec{BA}+2\vec{BA}.\vec{AC}+\vec{AC}.\vec{AC}$, par les propriétés du produit scalaire. En remplaçant le moyen terme par son expression trigonométrique (et en tenant compte du changement de signe lorsqu’on remplace $\vec{BA}$ par $\vec{AB}$), on obtient alors $$BC^2=AB^2+AC^2-2AB.AC.\cos\widehat{BAC}.$$
Les sommets du triangle jouant un rôle symétrique, nous avons démontré les trois propriétés suivantes.

Théorème d’Al-Kashi (loi des cosinus)
Si $ABC$ est un triangle plan, de côtés $a=BC$, $b=AC$ et $c=AB$, et d’angles $\alpha=\widehat{BAC}, \beta=\widehat{ABC}$ et $\gamma=\widehat{ACB}$, alors on a les égalités suivantes :
i) $a^2=b^2+c^2-2bc\cos\alpha$
ii) $b^2=a^2+c^2-2ac\cos\beta$
iii) $c^2=a^2+b^2-2ab\cos\gamma$.

La première relation est celle que nous avons démontrée, les deux autres s’obtiennent à partir de la première en échangeant les rôles de $A,B$ et $C$. Remarquons que ces relations restent valables :
1.Si on change l’orientation d’un ou plusieurs angles ($\widehat{CAB}$ au lieu de $\widehat{BAC}$, etc…), par les propriétés du cosinus d’un angle orienté
2.Pour tout triangle plan, en particulier pour un triangle plat, ou pour un triangle avec un angle obtus.

2.2.Dans l’autre sens

A partir de considérations trigonométriques usuelles sur les angles géométriques (c’est-à-dire non orientés), on peut démontrer dans l’autre sens l’expression trigonométrique du produit scalaire à partir de la loi des cosinus. On démontre alors celle-ci en utilisant les relations trigonométriques habituelles dans le triangle rectangle, grâce à l’introduction d’une hauteur et à l’application du théorème de Pythagore. Il est alors nécessaire d’introduire un raisonnement sur le signe du cosinus en fonction de l’existence ou non d’un angle obtus dans le triangle. Le schéma de l’approche utilisée est le suivant, pour un triangle acutangle, c’est-à-dire dans lequel tous les angles sont aigus (inférieurs à un angle droit).

Loi des cosinus
Dans un triangle $ABC$, où $\alpha$ est l’angle géométrique en $A$, on mène par le point $H$ de la droite $(AB)$ la hauteur $(HC)$ issue de $C$. Comme le triangle $AHC$ est rectangle en $H$, on a $AH=AC\cos\alpha$ et $CH=AC\sin\alpha$, et comme le triangle $BHC$ est rectangle en $H$, par le théorème de Pythagore on a $$\begin{eqnarray} BC^2 &=& BH^2+CH^2 = (AB-AC\cos \alpha)^2+(AC\sin\alpha)^2\\&=& AB^2-2AB.AC.\cos\alpha +AC^2\cos^2\alpha+AC^2\sin^2\alpha = AC^2+AB^2-2AB.AC.\cos\alpha,\end{eqnarray}$$ puisque $\cos^2\alpha+\sin^2\alpha=1$.

Expression trigonométrique du produit scalaire
Si $A,B,C$ sont trois points distincts du plan formant un triangle$ABC$ et $\alpha$ est l’angle géométrique entre $\vec{AB}$ et $\vec {AC}$, par définition, on a $BC^2=\vec{BC}.\vec{BC}=(\vec{BA}+\vec{AC}).(\vec{BA}+\vec{AC})=BA^2+2\vec{BA}.\vec{AC}+AC^2=AB^2+AC^2-2\vec{AB}.\vec{AC}$, par les propriétés du produit scalaire. Par la loi des cosinus appliquée au triangle $ABC$, on a $BC^2=AB^2+AC^2-2AB.AC.\cos\alpha$, d’où $\vec{AB}.\vec{AC}=AB.AC.\cos\alpha$ par ce qui précède.

On utilise des méthodes similaires dans le cas d’un triangle obtusangle (c’est-à-dire contenant un angle obtus, soit supérieur à un angle droit), et on peut obtenir la loi des cosinus sans distinguer le type de triangle en utilisant la puissance d’un point par rapport à un cercle et les mesures algébriques (voir Loi des cosinus – Wikipedia, sur le sujet et les approches historiques).

Conclusion

A partir de la définition analytique simplissime du produit scalaire de deux vecteurs du plan, et d’une définition naturelle des angles affines orientés et de leur cosinus et de leur sinus, on peut déduire l’expression trigonométrique du produit scalaire et de là la loi des cosinus, généralisation du théorème de Pythagore qu’on démontrait dans l’Antiquité et au Moyen-Âge par des méthodes géométriques. La relation entre produit scalaire et loi des cosinus souligne l’économie de l’approche analytique de la géométrie cartésienne, et la cohérence des aspects algébriques et trigonométriques de la géométrie euclidienne, entièrement recouvrés ici à partir de la seule définition des nombres réels.