Introduction

Lorsque nous avons introduit l’exponentielle circulaire, les fonctions trigonométriques cosinus et sinus ont été définies comme sa partie réelle et sa partie imaginaire. Nous en avons alors tiré les expressions analytiques : \(\cos x=\sum_{n=0}^{+\infty} (-1)^n\dfrac{x^{2n}}{(2n)!}\) et \(\sin x=\sum_{n=0}^{+\infty} (-1)^n\dfrac{x^{2n+1}}{(2n+1)!}\). Nous avons également retrouvé les propriétés essentielles \(\cos^2 t+\sin^2=1\), ainsi que \(\cos’t=-\sin t\) et \(\sin’t=\cos t\). A partir de ces seules propriétés, il est possible de définir le nombre \(\pi\), et d’étudier son rapport à l’exponentielle circulaire.

1.La fonction cosinus s’annule sur \(\mathbb R_+\)

Montrons tout d’abord que la fonction cosinus s’annule sur \(\mathbb R_+\). Par définition, on a \(\cos 0=1\) et si le cosinus ne s’annulait pas sur \(\mathbb R_+\), par continuité on aurait \(\cos x >0\) pour tout \(x\in\mathbb R_+\). Dans ce cas, la fonction sinus, de dérivée \(\cos x\), serait (strictement) croissante: choisissant un nombre réel \(a>0\), pour tout réel \(x>a\) on aurait \(\sin x>\sin a >0\), puisque \(\sin 0=0\). Considérons alors la fonction \(x\in I=]a,+\infty[\mapsto \cos x + x \sin a\), dont la dérivée est \(-\sin x+\sin a=\sin a-\sin x<0\). Sur l’intervalle \(I\), cette fonction serait ainsi strictement décroissante. Or, puisque la fonction cosinus est bornée et que \(\sin a>0\), cette fonction a pour limite \(+\infty\) lorsque \(x\) tend vers \(+\infty\). Ces deux propriétés sont mutuellement contradictoires, il faut donc en conclure que l’hypothèse est fausse : le cosinus s’annule sur \(\mathbb R_+\).

2.Le plus petit zéro positif du cosinus

Reformulons la conclusion de la démonstration précédente : comme \(\cos 0=1\), il existe au moins un nombre réel \(x>0\) tel que \(\cos x=0\). Par continuité de la fonction cosinus, on peut en dire un peu plus : comme \(\cos 0=1\neq 0\), le cosinus ne s’annule pas « au voisinage de \(0\) », c’est-à-dire que sur un intervalle ouvert \(I\) contenant \(0\), le cosinus ne s’annule pas. Autrement dit, la borne inférieure de l’ensemble \(X=\{x\in\mathbb R_+ : \cos x=0\}\) est un nombre strictement positif : notons-le \(a\). Par définition, on décrète alors que le nombre \(\pi\) est le nombre \(2\times a\), c’est-à-dire que \(a=\pi/2\). Or, les propriétés de la borne inférieure et la continuité de la fonction cosinus font que \(\cos a=0\) (par exemple, il existe une suite décroissante \((x_n)\) de nombres réels dans \(X\) qui tend vers \(a\)). En somme, le nombre \(a=\pi/2\) est le plus petit zéro positif de la fonction cosinus. Une définition analytico-géométrique du nombre \(\pi\) est donc qu’il est le double du plus petit zéro positif de la fonction \(\cos x\).

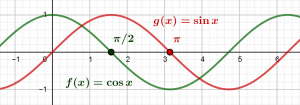
Le plus petit zéro positif de la fonction cosinus est par définition le nombre \(\pi/2\). Le nombre \(\pi\) est aussi le plus petit zéro strictement positif de la fonction sinus.

3.Le nombre \(\pi\), le sinus et l’exponentielle circulaire

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :

Pour aller plus loin

Commencer en mathématiques : Mathesis I.1 – Entrer dans l’Univers Mathématique