Les angles de vecteurs sont les angles orientés habituels de la géométrie euclidienne plane. Grâce aux ressources de la théorie naïve des ensembles, on les définit de manière purement algébrique grâce à une relation d’équivalence et aux rotations vectorielles du plan. L’opération de composition des rotations se transporte alors sur l’addition des angles.
1.Angles orientés de demi-droites : des angles de vecteurs
1.1.L’intuition des angles avec une orientation
Dans Le cercle trigonométrique : où Pythagore rencontre Thalès, nous avons considéré les angles orientés de manière intuitive, sans les définir rigoureusement. Un angle orienté est intuitivement une « ouverture » entre deux segments (par exemple dans une figure) ou en général deux demi-droites, basés au même point. Toutefois, cette ouverture est considérée avec son sens, horaire ou anti-horaire : si \(D_1\) et \(D_2\) sont deux demi-droites basées au même point \(M\), l’angle orienté entre \(D_1\) et \(D_2\) n’est pas le même que l’angle orienté entre \(D_2\) et \(D_1\). Un angle orienté étant déterminé par deux demi-droites, par une translation on peut toujours considérer que les demi-droites sont basées en l’origine du plan, le point \(O=(0,0)\).
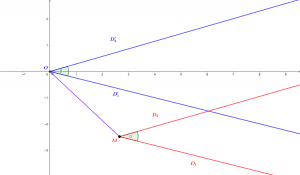
Par la translation de vecteur \(\overrightarrow{MO}\), les demi-droites \(D_1\) et \(D_2\) sont envoyées sur les demi-droites \(D_1’\) et \(D_2’\), et les angles orientés \(\alpha\) et \(\beta\) sont égaux
1.2.Remplacer les demi-droites par des vecteurs
Or, un couple de demi-droites basées en \(O\) est déterminé par les points d’intersection respectifs \(M_1\) et \(M_2\) de \(D_1\) et \(D_2\) avec le cercle \(S^1\). Mais les points du plan euclidien peuvent se concevoir aussi comme des vecteurs, donc le cercle trigonométrique \(S^1\) est à la fois l’ensemble des points \(M\) de \(\mathbb R^2\) tels que \(OM=1\) et l’ensemble des vecteurs unitaires du plan. Un vecteur \(\vec u=(x,y)\in\mathbb R^2\) est en effet dit unitaire s’il est de norme (euclidienne) \(1\), soit si \(||\vec u||=\sqrt{x^2+y^2}=1\). La donnée du couple \((D_1,D_2)\) peut donc être remplacée par celle des deux vecteurs unitaires \(\vec{u_1}=M_1\) et \(\vec{u_2}=M_2\). Autrement dit, nous aurions pu définir les angles orientés comme angles entre deux vecteurs unitaires, et c’est le point de vue que nous adoptons à présent.
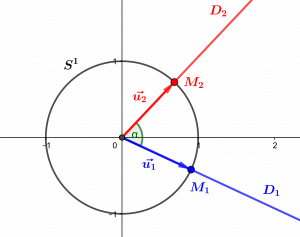
L’angle orienté \(\alpha\) entre les demi-droites \(D_1\) et \(D_2\) est l’angle des vecteurs \(\vec{u_1}\) et \(\vec{u_2}\) déterminés par l’intersection de \(D_1\) et \(D_2\) avec le cercle trigonométrique
1.3.Principe d’une définition par relation d’équivalence
Mathématiquement, les angles orientés se définissent rigoureusement par une relation d’équivalence, comme pour la construction de \(\mathbb Z\) à partir de \(\mathbb N\), de \(\mathbb Q\) à partir de \(\mathbb Z\) ou encore de \(\mathbb R\) à partir de \(\mathbb Q\). Un angle orienté étant déterminé par deux vecteurs unitaires, on considère qu’un couple \((\vec u,\vec v)\) de tels vecteurs représente un tel angle. Mais deux couples de vecteurs \((\vec u,\vec v)\) et \((\vec{u’},\vec{v’})\) peuvent représenter le même angle, lorsqu’intuitivement l’angle entre \(\vec u\) et \(\vec v\) est le même que l’angle entre \(\vec{u’}\) et \(\vec{v’}\). Précisément, c’est le cas exactement lorsqu’il existe une rotation qui transforme l’un en l’autre. On considère donc les angles orientés comme classes d’équivalence de couples de vecteurs unitaires.
1.4.Une définition mathématique rigoureuse
Donnons à partir de là une définition exacte des angles orientés ou angles de vecteurs. On considère l’ensemble \(E\) de tous les couples \((\vec u,\vec v)\) de vecteurs unitaires. Définissons une relation d’équivalence sur \(E\) en décrétant que deux éléments de \(E\), c’est-à-dire deux couples \((\vec u,\vec v)\) et \((\vec{u’},\vec{v’})\) de vecteurs unitaires sont équivalents si il existe une rotation vectorielle \(r\) qui « transforme \(\vec u\) en \(\vec {u’}\) et \(\vec v\) en \(\vec{v’}\) ». Un angle orienté ou angle de vecteurs est alors, par définition, une classe d’équivalence de couples \((\vec u,\vec v)\) de vecteurs unitaires pour cette relation. Autrement dit, c’est l’ensemble des couples \((\vec{u’},\vec{v’})\in E\) équivalents à un même couple \((\vec u,\vec v)\) donné. On note \([(\vec u,\vec v)]\) un tel angle, et l’un quelconque de ces couples est une représentation de l’angle \([(\vec u,\vec v)]\).
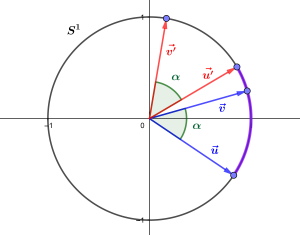
Les deux couples de vecteurs unitaires \((\vec{u},\vec{v})\) et \((\vec{u’},\vec{v’})\) représentent le même angle \(\alpha\), car une même rotation transforme \(\vec u\) en \(\vec{u’}\) et \(\vec v\) en \(\vec{v’}\).
2.Le cosinus et le sinus d’un angle de vecteurs
2.1.Représentation standard d’un angle de vecteurs
Si \(\vec\alpha=[(\vec u,\vec v)]\) est un angle de vecteurs, il en existe par définition de multiples représentations. Parmi celles-ci, un couple peut être distingué, qui est de la forme \((\vec i,\vec v’)\), où \(\vec i\) est le vecteur \((1,0)\) qui dirige la demi-droite des abscisses positives. En effet, le couple \((\vec u,\vec v)\) est une représentation de \(\vec\alpha\), et il existe toujours une rotation unique qui envoie un point quelconque de \(S^1\) sur un autre point donné de \(S^1\), donc un vecteur unitaire sur un vecteur unitaire donné. On considère alors la rotation \(r\) qui envoie \(\vec u\) sur \(\vec i=(0,1)\). Cette rotation transforme \(\vec v\) en un vecteur unitaire \(\vec{v’}\), et on a donc \(\vec\alpha=[(\vec i,\vec{v’})]\). Nous appellerons \((\vec i,\vec{v’})\) la représentation standard de l’angle (orienté) \(\vec\alpha\).
2.2.Coordonnées circulaires d’un angle de vecteurs
Etant donné un angle de vecteurs $\alpha$, nous pouvons désormais en choisir une représentation standard, sous la forme du couple $(\vec i\vec v)$, avec $\vec i=(1,0)$ et $\vec v=(a,b)$ disons. Puisque, par définition, le vecteur $\vec v$ est de norme $1$, il détermine également un point du cercle trigonométrique, notons-le $M=(a,,b)$ pour insister sur la dualité entre les points et les vecteurs. Mais nous avons introduit avec le cercle trigonométrique les coordonnées circulaires d’un angle orienté comme celle du point qu’il détermine sur ce cercle. Ainsi, nous pouvons définir de même les coordonnées circulaires d’un angle de vecteurs comme les coordonnées du point que sa représentation standard détermine sur le cercle trigonométrique : avec les notations présentes, par définition le cosinus de $\alpha$, noté $\cos\alpha$, est l’abscisse de $M$, soit le nombre réel $a$, tandis que le sinus de $\alpha$, noté $\sin\alpha$, est par définition l’ordonnée de $M$, soit le nombre réel $b$. Le cosinus et le sinus d’un angle orienté s’obtiennent donc, à partir d’une représentation quelconque, grâce à une rotation qui permet d’en identifier la représentation standard.
2.3.Produit scalaire et déterminant
L’angle de vecteurs $\alpha=[(\vec u,\vec v)]$ étant donné, avec $\vec u=(a,b)$ et $\vec v=(c,d)$ unitaires, comment déterminer son cosinus et son sinus ? C’est possible de manière purement analytique à partir de la représentation standard $\alpha=[(\vec i,\vec v’)]$, avec $\vec v’=r(\vec i)$, $r$ étant l’unique rotation qui envoie $u$ sur $v$. La rotation $r$ étant de la forme $(x,y)\in\mathbb R^2\mapsto (\lambda x-\mu y,\lambda y+\mu x)$ pour des nombres réels $\lambda,\mu$ uniques (voir Rotations vectorielles du plan), ces coefficients doivent vérifier $r(\vec u)=\vec v$, soit le système suivant en $\lambda$ et $\mu$ : \begin{eqnarray} \lambda a-\mu b &= &c\\
\lambda b+\mu a&=&d,\end{eqnarray} dont l’unique solution est $(\lambda=ac+bd,\mu=ad-bc)$. Or, on reconnaît ici le produit scalaire $\vec u.\vec v=ac+bd$ et le déterminant $det(\vec u,\vec v)=ad-bc$ des vecteurs $\vec u$ et $\vec v$ ! Autrement dit, pour calculer le cosinus et le sinus d’un angle de vecteurs $[(\vec u,\vec v)]$, il suffit de calculer leur produit scalaire et leur déterminant.
2.4.Rotations vectorielles et angles orientés
La construction même des angles de vecteurs montre qu’angles orientés et rotations vectorielles sont étroitement liés : il s’agit en fait essentiellement des même objets, présentés différemment, ce que permet de conceptualiser la théorie des groupes. Il suffit ici de préciser que les rotations « préservent les angles » : si $r$ est une rotation vectorielle, et si $\alpha=[(\vec u,\vec v)]$ est un angle de vecteurs, alors l’angle de vecteurs $[(r(\vec u),r(\vec v)]$ est encore l’angle $\alpha$ : c’est vrai précisément par définition des angles de vecteurs !
3.Le groupe des angles de vecteurs
3.1.Bijection entre les rotations et les angles
Il existe une bijection entre l’ensemble \(\mathcal R\) des rotations vectorielles du plan et le cercle trigonométrique \(\mathcal S^1\) (revoir Rotations vectorielles du plan : l’approche « analytique »), qui associe à une rotation \(r\) décrite comme \(r(x,y)=(ax-by,bx+ay)\) le point ou vecteur \((a,b)\). Il est donc possible d’associer aussi à une telle rotation un angle de vecteurs : en considérant le vecteur \(\vec u=r(\vec i)\), soit \(\vec u=(a,b)\) (le point de \(S^1\) déterminé par \(r\)…) on obtient l’angle \([(\vec i,\vec u)]\). A partir de la bijection entre \(\mathcal R\) et \(S^1\), on démontre facilement qu’on obtient ainsi une nouvelle bijection \(f\) entre l’ensemble des rotations vectorielles et l’ensemble \(\mathcal A\) des angles de vecteurs. Si \(r\) est une rotation, l’angle correspondant, \(f(r)\), est par définition l’angle de la rotation \(r\).
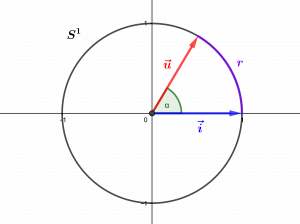
L’angle de vecteurs \(\alpha=[(\vec i,\vec u)]\) est l’angle de la rotation \(r\) qui envoie \(\vec i\) sur \(\vec u\)
3.2.Addition et soustraction des vecteurs
Bienvenue sur La Règle et le Compas ! Pour lire les articles du blog en intégralité, merci de vous connecter. Si ce n'est déjà fait, vous pouvez vous inscrire librement ici sur MATHESIS.
Pour aller plus loin

0 commentaires