Les relations entre les propriétés de monotonie, continuité et dérivation d’une fonction d’une variable réelle, permettent de dériver formellement la bijection inverse d’une fonction injective et dérivable. L’exemple le plus représentatif est peut-être celui de la fonction exponentielle, réciproque du logarithme népérien.

Monotonie, continuité, dérivation

Dans la théorie élémentaire des fonctions d’une variable réelle, on étudie les relations subtiles entre les fonctions monotones, continues et dérivables, en lien étroit avec la « topologie » de la droite réelle, c’est-à-dire les intervalles où ces fonctions sont définies. Rappelons qu’un intervalle de l’ensemble \(\mathbb R\) est un sous-ensemble \(I\subseteq \mathbb R\) tel que pour tous \(a,b\in I\), le segment \([a,b]=\{x\in \mathbb R : a\leq x\leq b\}\) est tout entier inclus dans \(I\).

Par exemple, on démontre que si \(f:I\to\mathbb R\) est une fonction continue définie sur un intervalle \(I\), alors l’image \(f(I)\) de la fonction \(f\) est aussi un intervalle. On sait aussi qu’une telle application est injective si et seulement si elle est strictement monotone (c-à-d strictement croissante ou strictement décroissante) ! Et dans ce cas, lorsque l’intervalle \(I\) est ouvert, l’image \(f(I)\) est aussi un intervalle ouvert. Or, on étude les variations d’une telle fonction, lorsque cela est possible, grâce à sa dérivée (voir Qu’est-ce que la dérivée d’une fonction ? Définition et interprétation géométrique): une fonction dérivable \(f:I\to\mathbb R\) définie sur un intervalle ouvert \(I\) est monotone sur \(I\) si et seulement si \(f'(t)\) garde un signe constant sur \(I\), positif si \(f\) est croissante, négatif si \(f\) est décroissante.

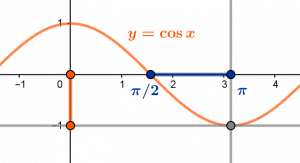
La fonction \(\cos x\) est strictement décroissante sur l’intervalle ouvert \(I=]\pi/2,\pi[\) et l’image de cet intervalle par le cosinus est l’intervalle ouvert \(]-1,0[\)

A partir de la définition de la dérivée d’une fonction, on peut également dériver une fonction composée (voir par exemple Wikipedia : dérivation des fonctions composées). Si \(f:I\to \mathbb R\) et \(g:J\to\mathbb R\) sont deux fonctions définies sur des intervalles ouverts \(I\) et \(J\), et dérivables, et si \(f(I)\subseteq J\), alors la fonction \(g\circ f\) est définie et on a \((g\circ f)'(x)=g'(f(x)).f'(x)\) pour tout \(x\in I\).

Dériver la bijection inverse

On peut aisément tirer de ces propriétés l’expression de la dérivée d’une bijection inverse dans certains cas. En effet, si \(f:I\to \mathbb R\) est une fonction dérivable et injective, définie sur un intervalle ouvert \(I\), \(f\) est continue donc son image \(f(I)\) est un intervalle ouvert \(J\). En la considérant comme application de \(I\) dans \(J\), notons \(g:J\to I\) sa bijection réciproque. Par définition, on a \(f\circ g(x)=x\) pour tout \(x\in J\), c’est la fonction « identique » \(x\in J\mapsto x\in J\). Si \(g\) est dérivable, la dérivée de \(f\circ g\) est donc la dérivée de la fonction identique, qui vaut \(1\), et par la formule de dérivation des fonctions composées on peut donc écrire \[1=(f\circ g)'(x)=f'(g(x)).g'(x)\] pour tout \(x\in J\).

En fait, dans cette situation et avec les mêmes notations on peut montrer que la fonction \(g:J\to I\) est alors dérivable en tout point \(x\in J\) pour lequel \(f'(g(x))\neq 0\) et en ce point, la formule précédente – c’est-à-dire \(1=(f\circ g)'(x)=f'(g(x)).g'(x)\) – nous donne la dérivée \[g'(x)=\dfrac{1}{f'(g(x))}.\] En particulier, si \(f:I\to\mathbb R\) est dérivable et strictement monotone, et si sa dérivée \(f’\) ne s’annule jamais, alors sa bijection réciproque \(g:J\to I\) est dérivable en tout point \(x\in J\) et la formule précédente nous donne une expression générale de sa dérivée en tout point.

La bijection inverse de la fonction cube \(f:x\in\mathbb R\mapsto x^3\in\mathbb R\) est la fonction racine cubique \(g:x\in\mathbb R\mapsto \sqrt[3]x\in\mathbb R\); la dérivée de \(f\) est \(f'(x)=3x^2\) et en tout point \(x\neq 0\) on a \(f'(g(x))=3(\sqrt[3]x)^2\neq 0\), où la dérivée de \(g\) est donc \(g'(x)=\dfrac{1}{3(\sqrt[3]x)^2}\). Ici la fonction \(f\) est strictement croissante, et pourtant sa dérivée s’annule en \(x=0\), point où la fonction réciproque \(g\) n’est pas dérivable.

Exemple : dériver la fonction exponentielle

Comme application de la formule de dérivation d’une bijection inverse, nous allons montrer que la dérivée de la fonction exponentielle est égale à la fonction elle-même, c’est-à-dire que pour tout \(x\in\mathbb R\), on a \[\exp'(x)=\exp(x).\]

Pour cela, rappelons la définition usuelle de la fonction exponentielle. Par les propriétés de l’intégrale de Riemann, on définit d’abord la fonction Logarithme (népérien) \(\ln:\mathbb R_+^*\to \mathbb R\), par l’expression \[\ln(x)=\int_1^x \dfrac 1 t \ dt\] pour tout nombre réel \(x>0\). Autrement dit, le Logarithme est la primitive de la fonction \(x\in \mathbb R_+^*\mapsto 1/x\) qui s’annule en \(x=1\). On démontre alors que cette application est strictement croissante et que \(\lim\limits_{x\to 0} \ln(x)=-\infty\) et \(\lim\limits_{x\to +\infty} \ln(x)=+\infty\), si bien que comme \(\ln\) est par définition dérivable, de dérivée \(1/x\), il s’agit d’une bijection de \(\mathbb R_+^*\) sur \(\mathbb R\). Par définition, la fonction exponentielle est alors la bijection réciproque du Logarithme, soit l’unique application \(\exp:\mathbb R\to \mathbb R_+^*\) telle que pour tous \(t\in \mathbb R_+^*\) et \(x\in \mathbb R\), on ait \(\exp(\ln(t))=t\) et \(\ln(\exp(x))=x\).

Appliquons alors le théorème énoncé et la formule écrite précédemment avec \(f=\ln\), \(I=\mathbb R_+^*\), \(g=\exp\) et \(J=\mathbb R\). Comme \(\ln\) est strictement croissante et dérivable, et comme \(ln'(t)=1/t>0\) pour tout \(t>0\), sa réciproque \(\exp\) est dérivable, et sa dérivée en tout point \(x\in \mathbb R\) est donnée par \[\exp'(x)=\dfrac 1 {\ln'(\exp(x))}=\dfrac{1}{1/\exp(x)}=\exp(x),\] ce que nous voulions démontrer.

Une partie du graphe de la fonction logarithme \(\ln\) est représentée en bleu, et en rouge une partie du graphe de sa bijection inverse, la fonction exponentielle. Les deux fonctions sont strictement croissantes comme le prédit la théorie, et leurs graphes sont symétriques par rapport à la droite d’équation \(y=x\), puisqu’elle sont réciproques. La dérivée de la fonction \(\exp\) est égale à la fonction en tout point, donc la pente de la tangente au point \((x,\exp(x))\) est la valeur de la fonction, soit \(\exp(x)\), ce qui donne au graphe de cette fonction son allure caractéristique. En particulier, la pente en \(x=1\) est le nombre \(e\), base de l’exponentielle.

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :

Pour aller plus loin

Commencer en mathématiques : Mathesis I.1 – Entrer dans l’Univers Mathématique