L’intuition visuelle à travers laquelle nous représentons le plan euclidien suggère que nous puissions l’orienter selon un sens de rotation. Cette intuition reflète une définition mathématique rigoureuse de l’orientation du plan, qui consiste à choisir une base, et donc implicitement un angle de vecteurs. En fait, choisir une orientation correspond au choix d’une famille de bases orthonormées qui se déduisent l’une de l’autre par une isométrie directe. On peut alternativement le considérer comme le choix d’une famille de bases quelconques qui se déduisent l’une de l’autre par une transformation de détermination strictement positif.

1.Orienter le plan : intuition, représentation et vecteurs de base

1.1.Deux sens de rotations sont possibles dans le plan

Choisissons un point du plan euclidien et traçons deux demi-droites dans des directions différentes à partir de ce point. L’intuition nous dit que nous pouvons « passer » de l’une des demi-droites à l’autre par deux rotations différentes, en choisissant un sens ou un autre. Le sens « direct » ou « trigonométrique », selon notre représentation habituelle du plan, correspond au « sens inverse des aiguilles d’une montre ». Le sens « indirect » correspond à l’autre sens. Cette idée, qu’il existerait deux sens de rotations possibles dans le plan, correspond à un concept mathématique rigoureux, celui d’orientation du plan euclidien.

1.2.La représentation visuelle de l’orientation est une convention

Le plan euclidien (c’est-à-dire l’intuition sous-jacente à la géométrie d’Euclide) est représenté en mathématique moderne par le produit cartésien \(\mathbb R^2\). Le couple de vecteurs \(\vec i=(1,0)\) et \(\vec j=(0,1)\), appelé base canonique, est traditionnellement représenté comme dans la figure suivante et une telle représentation fixe dans notre esprit une « orientation » : le « plus petit angle » (l’angle de plus petite mesure principale) entre les deux vecteurs \(\vec i\) et \(\vec j\) détermine le sens « trigonométrique ». Il faut garder à l’esprit qu’il ne s’agit ici que d’un choix de représentation, qui considère l’ordre croissant des abscisses de gauche à droite ! Si nous représentions les abscisses dans l’autre sens, alors notre représentation de l’orientation déterminée par \(\vec i\) et \(\vec j\) serait inversée; nous pourrions également représenter les abscisses verticalement et les ordonnées horizontalement. Ceci signifie qu’il n’existe pas de représentation visuelle privilégiée de cette orientation « standard ».

1.3.L’ordre des vecteurs naturels de base définit une orientation

Cependant, et indépendamment de notre représentation visuelle, le choix de \(\vec i\) et \(\vec j\), dans cet ordre, détermine bien une orientation privilégiée, dans un sens mathématique précis. Dit autrement, l’orientation est déterminée par l’ordre \(\vec i,\vec j\), ce qui signifie que prendre les deux vecteurs dans l’ordre inverse, soit \(\vec j,\vec i\), détermine une autre orientation. Comme il n’existe que deux orientations possibles du plan (ainsi que nous le verrons), l’ordre choisi sur ces deux vecteurs constitue une définition possible d’une orientation du plan.

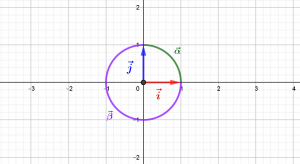
Les vecteurs \(\vec i=(1,0)\) et \(\vec j=(0,1)\) déterminent une orientation du plan. L’angle \(\vec\alpha\) déterminé par la base canonique \((\vec i,\vec j)\) a pour mesure \(\pi/2\), il détermine un sens « direct » naturel, tandis que l’angle \(\vec\beta\) déterminé par le couple \((\vec j,\vec i)\) a pour mesure positive \(3\pi/2\), il représente un sens « indirect » naturel.

2.Définition mathématique de l’orientation du plan

2.1.On oriente le plan euclidien par le choix d’une base

Nous voulons donner ici un sens mathématique précis à cette dernière idée : les deux couples (différents) formés avec les deux vecteurs \(\vec i\) et \(\vec j\) de la base canonique de \(\mathbb R^2\), déterminent les deux (seules) orientations possibles du plan. Rappelons que ce couple de deux vecteurs est appelé une « base de l’espace vectoriel \(\mathbb R^2\) » parce qu’ils permettent de représenter de manière univoque n’importe quel vecteur \(\vec u=(x,y)\) de \(\mathbb R^2\) sous la forme \(\vec u=x.\vec i+y.\vec j\). La raison essentielle en est que ces deux vecteurs sont non nuls et non colinéaires (c’est-à-dire qu’ils ont des directions différentes). Or, il paraît évident que le choix d’une autre base détermine aussi une orientation : deux vecteurs d’une base déterminent un angle orienté, ni nul ni plat, et la mesure principale de cet angle, inférieure ou supérieure à \(\pi\), détermine une orientation, respectivement « directe » ou « indirecte » (par rapport à la base canonique, prise comme référence). Il nous faut donc établir précisément la relation entre bases du plan et orientation du plan, et comment ces notions se rapportent aux vecteurs \(\vec i\) et \(\vec j\).

2.2.L’angle déterminé par une base du plan

A une base quelconque \(B=(\vec u,\vec v)\) du plan euclidien, on peut associer un angle de vecteurs. En effet, en divisant \(\vec u\) et \(\vec v\) par leur norme, on obtient un couple de vecteurs unitaires \(B’=(\vec{u’},\vec{v’})\), qui déterminent par définition un tel angle \(\vec\alpha=[(\vec{u’},\vec{v’})]\), appelons-le l’angle déterminé par \(B\). Comme \(\vec{u}\) et \(\vec{u’}\) d’une part, \(\vec v\) et \(\vec{v’}\) d’autre part, ont la même direction, \(B’\) est également une base de \(\mathbb R^2\). Autrement dit, les vecteurs \(\vec{u’}\) et \(\vec{v’}\) sont non nuls et non colinéaires, donc la mesure principale de l’angle déterminé par \(B\), autrement dit le nombre \(s\in [0,2\pi[\) qui représente cette mesure, est différent de \(0\) et de \(\pi\). La valeur de \(s\) est alors comprise soit dans l’intervalle ouvert \(]0,\pi[\), soit dans l’intervalle ouvert \(]\pi,2\pi[\). L’intuition sous-jacente à l’idée d’une base \(B\) orientée « dans le sens direct » correspond à la situation où la mesure principale \(s\) de l’angle \(\vec\alpha\) est la plus petite possible, soit \(0<s<\pi\). Dans le cas contraire, c’est-à-dire lorsque \(\pi<s<2\pi\), on considère que la base \(B\) est orientée « dans le sens indirect ». Bien sûr, en permutant les vecteurs \(\vec u\) et \(\vec v\), on « change le sens de l’orientation », puisque l’angle \(\vec\alpha\) est changé en \(-\vec\alpha\), dont la mesure principale est \(2\pi -s\).

2.3.Interprétation algébrique de l’orientation d’une base

Choisir une orientation du plan peut donc se concevoir comme le choix d’une base du plan. La mesure principale de l’angle déterminé par les vecteurs de cette base détermine par définition si l’orientation est directe ou indirecte. Le cas de la base canonique fournit bien une orientation directe, puisque l’angle \([(\vec i,\vec j)]\) a pour mesure principale \(\pi/2\), qui se trouve dans l’intervalle \(]0,\pi[\). Il est en fait possible de donner une caractérisation de l’orientation déterminée par une base quelconque, en la rapportant à la base canonique. Etant donnée une base \(B=(\vec u,\vec v)\), nous avons en effet évoqué l’existence d’une transformation linéaire permettant de passer de la base canonique à la base \(B\) : il s’agit de l’application \(f:(x,y)\in\mathbb R^2\mapsto (ax+by,cx+dy)\), si \(\vec u=(a,c)\) et \(\vec v=(b,d)\). En général, nous avons évoqué comment le déterminant d’une telle application \(f\), soit le nombre \(\Delta=ad-bc\), permet de caractériser les situations où les vecteurs \((a,c)\) et \((b,d)\) forment une base, à savoir lorsque \(ad-bc\neq 0\). Dans ce cas, le déterminant permet également de déterminer l’orientation de la base en fonction de son signe : on peut démontrer que la base \(B\) est directe lorsque \(\Delta>0\), indirecte lorsque \(\Delta<0\).

La base \(B=(\vec u,\vec v)\) formée des vecteurs \(\vec u=(a,c)\) et \(\vec v=(b,d)\) détermine une orientation directe, puisque l’angle déterminé par \(B\) est de mesure principale dans l’intervalle \(]0,\pi[\), ce qui est confirmé par le calcul de \(\Delta=ad-bc\), strictement positif. En revanche, la base \((\vec v,\vec w)\) est orientée de manière indirecte, puisque la mesure principale de l’angle qu’elle détermine est dans l’intervalle \(]\pi,2\pi[\).

3.Orientation par les bases orthonormées

3.1.Caractérisation de l’orientation induite par une base orthonormée

En introduisant les bases orthonormées, nous avons précisément distingué entre les bases orthonormées directes \((\vec u,\vec v)\), pour lesquelles l’angle \(\vec\alpha=[(\vec u,\vec v)]\) a pour mesure principale \(\pi/2\), et les bases orthonormées indirectes \((\vec u,\vec v)\), pour lesquelles l’angle \(\vec\alpha=[(\vec u,\vec v)]\) a pour mesure \(-\pi/2\). Nous retrouvons ce cas comme cas particulier de l’orientation telle qu’elle est définie ici à partir d’une base, puisqu’une base orthonormée est indirecte lorsque sa mesure principale est \(2\pi-\pi/2=3\pi/2\), dans l’intervalle \(]\pi,2\pi[\). L’interprétation de l’orientation par le déterminant est particulièrement simple dans ce cas : si \(B=(\vec u,\vec v)\) est une base orthonormée et \(f\) est sa transformation orthogonale associée, la base \(B\) est directe lorsque le déterminant \(\Delta\) de \(f\) vaut \(1\), elle est indirecte lorsque \(\Delta\) vaut \(-1\). Cette caractérisation très simple de l’orientation du plan fait qu’on définit souvent celle-ci à partir des bases orthonormées, en fait à partir de classes d’équivalences de celles-ci.

3.2.Bases orthonormées équivalentes : deux solutions possibles

Etant données deux bases orthonormées quelconques \(B\) et \(B’\), la transformation \(f\) de \(B\) à \(B’\) est toujours une isométrie vectorielle, et deux cas seulement peuvent alors se présenter. Soit \(f\) est directe (c’est-à-dire de déterminant \(1\)), soit \(f\) est indirecte (c’est-à-dire de déterminant \(-1\)). Dans le premier cas, c’est-à-dire celui où \(f\) est une rotation, nous dirons que \(B\) et \(B’\) sont équivalentes. Une classe d’équivalence de bases d’orthonormée est alors simplement un ensemble de bases orthonormées équivalentes à une base donnée. Or, une base orthonormée \(B\) quelconque étant donnée, la transformation de la base canonique \(C=(\vec i,\vec j)\) à \(B\) est soit directe, soit indirecte, et il s’agit des deux seuls cas possibles ! Ainsi, il n’existe que deux classes d’équivalence, l’ensemble des bases orthonormées qui se déduisent de \(C\) par une rotation, et l’ensemble des bases orthonormées qui se déduisent de \(C\) par une symétrie (transformation de déterminant \(-1\)). On définit savamment une orientation du plan comme le choix d’une de ces classes, qui sert alors de référence.

3.3.Définir l’orientation par l’équivalence de bases quelconques

Cette manière de procéder à partir des bases orthonormées convient aussi à n’importe quel type de bases. Si \(B\) et \(B’\) sont deux bases quelconques du plan, la transformation linéaire \(f\) de \(B\) à \(B’\) n’est pas une isométrie en général, mais elle possède toujours un déterminant \(\Delta\) non nul. Ici aussi on peut naturellement distinguer deux cas : soit \(\Delta >0\) (la transformation \(f\) est « directe » ou « préserve l’orientation »), soit \(\Delta <0\) (la transformation \(f\) est « indirecte » ou « renverse l’orientation »). Nous pouvons aussi dire que \(B\) et \(B’\) sont équivalentes si \(\Delta>0\), et en prenant à nouveau la base canonique \(C=(\vec i,\vec j)\) comme référence, distinguer les bases qui s’en déduisent par des transformations directes, de celles qui s’en déduisent par des transformations indirectes. Nous obtenons alors à nouveau deux classes d’équivalence, et le choix de l’une d’entre elles détermine aussi une orientation du plan.

La base orthonormée \(B=(\vec u,\vec v)\) se déduit de la base canonique \(C=(\vec i,\vec j)\) par une rotation, elle définit donc la même orientation; en revanche, la base orthonormée \(B’=(\vec u,-\vec v)\) se déduit de \(C\) par une transformation indirecte (une symétrie et une rotation), donc elle définit l’orientation opposée.

Conclusion : l’orientation du plan demeure un choix mathématique

Il existe plusieurs manières, mathématiquement rigoureuses, de définir une orientation du plan euclidien \(\mathbb R^2\). Même si il existe une orientation naturelle privilégiée, celle qui est donnée par la base canonique et les autres bases, orthonormées ou non, qui lui sont équivalentes par une transformation directe, orienter le plan résulte d’un choix, soit d’une base, soit d’une classe d’équivalence de bases du plan. Mais il n’existe jamais que deux choix possibles.