Quelle est l’opération inverse de la dérivée d’une fonction ? Une première réponse à cette question consiste à intégrer une fonction qu’on veut pouvoir considérer comme dérivée, afin d’en construire une primitive. Cette problématique conduit naturellement à l’intuition géométrique sous-jacente à la définition de l’intégrale de Riemann sur un segment, à partir d’approximations inférieures et supérieures simples. Les fonctions monotones et continues par morceaux sont intégrables au sens de Riemann, et en particulier toute fonction continue est la dérivée d’au moins une fonction, obtenue par intégration.

1.Trouver l’opération inverse de la dérivée

Si $f:I\to\mathbb R$ est une fonction numérique définie sur un intervalle réel $I$, et si $f$ est dérivable sur $I$, sa fonction dérivée $f’:I\to \mathbb R$ est un objet mathématique essentiel, dont l’étude permet d’identifier les variations de $f$ (voir Qu’est-ce que la dérivée d’une fonction ?). En effet, la fonction $f$ est croissante sur toute partie de $I$ où sa dérivée $f’$ est positive, elle est décroissante sur toute partie de $I$ où sa dérivée est négative. En général, la dérivée de $f$ et ses dérivées successives éventuelles fournissent des informations analytiques et géométriques précieuses sur la fonction elle-même. Par exemple, le développement de Taylor de $f$ en un point $x_0$ permet d’exprimer la fonction « autour de $x_0$ » à partir des valeurs de ses premières dérivées en $x_0$. Mais dans l’autre sens, l’existence d’une « opération » inverse de la dérivation est aussi une question naturelle, qu’on peut formuler de la manière suivante :

Question
Etant donnée une fonction numérique $f:I\to \mathbb R$ définie sur un segment, existe-t-il une fonction $F:I\to \mathbb R$ telle que $F’=f$ ?

Si une telle fonction $F$ existe, on dit que c’est une primitive de $f$. Une réponse à la question consiste alors à intégrer la fonction $f$ sur l’intervalle $I$, qu’on choisit en principe et en premier lieu comme un segment.

2.Le principe de l’intégrale sur un segment

2.1.L’intégrale de Riemann et la recherche d’une primitive

Bernhard Riemann est un mathématicien allemand du 19ième siècle, qui a notamment cherché à identifier quelles fonctions étaient intégrables. Intégrer une fonction, c’est en quelque sorte en réaliser une « moyenne continue », et Riemann a laissé son nom à l’intégrale élémentaire des fonctions réelles définies sur un segment. L’intérêt de l’intégrale de Riemann pour répondre à la question posée à la section précédente, est que l’intégration d’une fonction typique $f:[a,b]\to\mathbb R$, c’est-à-dire continue (où $a,b$ sont des nombres réels tels que $a\leq b$), peut fournir une primitive de $f$. En effet, pour une telle fonction l’aire (au sens algébrique) comprise entre le graphe de $f$, l’axe des abscisses, une droite verticale d’équation $x=x_0$ avec $x_0\in [a,b]$ et une autre droite verticale d’équation $x=t$ avec $t\in [a,b]$ variable, définit une fonction $F$ de la variable $t$, et dont la dérivée en chaque point $t\in [a,b]$ est $f$ : autrement dit, $F$ est une primitive de $f$.

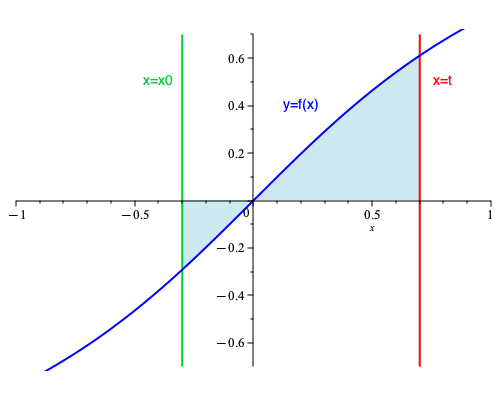
2.2.Relation entre l’intégrale et la primitive

Pour nous en convaincre, considérons une approximation de cette aire, et choisissons pour cela un autre élément $t_0$ de $[a,b]$ : l’aire comprise entre l’axe des abscisses et les droites verticales d’équation $x=t_0$ et $x=t$ est par définition $F(t)-F(t_0)$. Soit alors $m$ le minimum des valeurs de $f(x)$ sur le segment $[t_0,t]$, et $M$ le maximum de ces valeurs : l’aire $F(t)-F(t_0)$ est comprise entre $(t-t_0).m$ et $(t-t_0).M$, autrement dit pour tout $t\neq t_0$ on peut écrire $$m\leq \dfrac{F(t)-F(t_0)}{t-t_0} \leq M.$$ On reconnaît au membre du milieu le rapport de monotonie de la fonction $F$ entre $t_0$ et $t$ : celle-ci est dérivable si et seulement si ce rapport possède une limite finie lorsque $t$ tend vers $t_0$, et cette limite est alors, par définition, $F'(t_0)$. Mais par définition de $m$ et de $M$, lorsque $t$ tend vers $t_0$ les nombres $m$ et $M$ – qui dépendent de $t$ – tendent vers la même valeur, à savoir $f(t_0)$, de sorte qu’à la limite, on a $f(t_0)=m=F'(t_0)=M$. En d’autres termes, la fonction $F$ est dérivable en $t_0$ et $F'(t_0)=f(t_0)$, c’est donc une primitive de $f$.

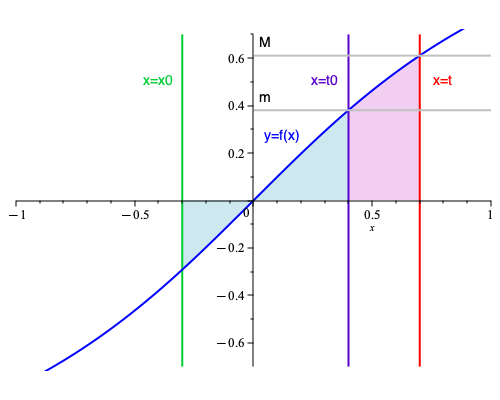
3.L’intégrale selon Riemann

3.1.Le principe de l’intégrale : réaliser des approximations

L’explication précédente est schématique : d’une part, l’aire entre la courbe, l’axe des abscisses et les droites verticales n’est pas définie (c’est précisément l’intégrale), d’autre part nous avons fait l’hypothèse que la fonction $f$ est continue. Or, la continuité n’est pas une hypothèse nécessaire pour intégrer une fonction, et nous devons en fait définir l’intégrale à partir de la notion de fonction intégrable. Celle-ci repose sur l’intuition précédente, c’est-à-dire l’approximation de l’aire à définir sur des segments de taille arbitraire divisant le domaine $[a,b]$ d’une fonction numérique $f:[a,b]\to \mathbb R$. On utilise le concept suivant :

Définition 1
Une subdivision de $[a,b]$ est une suite finie de points $a_0,a_1,\ldots,a_{n},a_{n+1}$ de $[a,b]$ telle que $a=a_0<a_1<\ldots <a_{n}<a_{n+1}=b$.

Les subdivisions sont alors utilisées pour construire des approximations de la fonction $f$ à partir de fonctions « simples », c’est-à-dire constantes sur chaque intervalle d’une subdivision, et dont on peut définir l’intégrale comme une aire élémentaire, c’est-à-dire celle d’un rectangle :

Définition 2
i) Une fonction $g:[a,b]\to \mathbb R$ est dite en escalier si il existe une subdivision $a=a_0<a_1<\ldots <a_n<a_{n+1}=b$ de $[a,b]$ telle que $g$ est constante sur chaque intervalle ouvert $]a_i,a_{i+1}[$, $i=0,\ldots,n.$
ii) Si $g$ est une telle fonction, l’intégrale de $g$ est par définition le nombre réel $\sum_{i=0}^{n} g(x_i).(a_{i+1}-a_i)=g(x_0).(a_1-a)+g(x_1).(a_2-a_1)+\ldots+g(x_{n-1}).(a_n-a_{n-1})+g(x_n).(a_{n+1}-a_n),$ où $x_i\in ]a_i,a_{i+1}[$ pour tout $i=0,\ldots,n.$

Dans cette définition, les valeurs $g(x_i)$ ne dépendent pas du choix de $x_i$ puisque $g$ est constante sur chaque intervalle ouvert de la subdivision. De plus, si $g$ peut être décrite à l’aide d’une autre subdivision, on obtient la même valeur pour l’intégrale : celle-ci est donc bien définie, ne dépend pas des valeurs de $g$ aux points de la subdivisino, et on note $\int_a^b g(t)\ dt$ l’intégrale d’une fonction en escalier $g:[a,b]\to \mathbb R$.

3.2.L’intégrabilité comme convergence des approximations

Intuitivement, la fonction $f$ sera alors considérée comme « intégrable » si l’aire comprise entre son graphe et l’axe des abscisses est « calculable ». En particulier, cela signifie que cette aire est supérieure à l’intégrale de certaines fonctions en escalier – dont la valeur est (presque) partout inférieure à celle de $f$, formant un ensemble $E^-$ – et inférieure à l’intégrale d’autres fonctions en escalier – dont la valeur est (presque) partout supérieure à celle de $f,$ et formant un ensemble $E^+$. On peut en fait utiliser ce critère comme définition rigoureuse de l’intégrabilité de $f$ : celle-ci consiste alors à ce que l’on peut choisir des approximations inférieure et supérieure dont les intégrales sont arbitrairement proches, précisément :

Définition 3
La fonction $f:[a,b]$ est dite intégrable (au sens de Riemann), si pour tout nombre réel $\epsilon >0$, il existe des fonctions en escalier $g\in E^-$ et $h\in E^+$ telles que $|\int_a^b h(t)\ dt-\int_a^b g(t)\ dt|\leq \epsilon.$

Par choix des fonctions $g$ et $h$, l’intégrale de $h$ est toujours supérieure à celle de $g$ : l’inégalité du critère s’écrit plus simplement sous la forme $\int_a^b h(t)\ dt-\int_a^b g(t)\ dt\leq \epsilon.$ On reconnaît ici l’usage d’une propriété « infinitésimale », comme dans la définition de la continuité. Une autre formulation possible est que le supremum des intégrales de fonctions de $E^-$ et égal à l’infimum des intégrales de fonctions de $E^+$. Cette approche permet de définir l’intégrale d’une fonction intégrable comme la valeur limite des intégrales de $g\in E^-$, qui est aussi la valeur limite des intégrales de $h\in E^+$ :

Proposition 1
Une fonction $f:[a,b]\to\mathbb R$ est intégrable si et seulement si le supremum des intégrales $\int_a^b g(t)\ dt$ pour $g\in E^-$ est égal à l’infimum des intégrales $\int-a^b h(t)\ dt$ pour $h\in E^+$.

Ainsi, lorsque $f$ est Riemann-intégrable, on appelle intégrale de $f$ ce nombre commun, qu’on note $\int_a^b f(t)\ dt$, et on définit également l’intégrale de $f$ « dans l’autre sens » (rappelons que jusqu’ici, nous avons supposé que $a\leq b$) en posant $\int_b^a f(t)\ dt=-\int_a^b f(t)\ dt.$ Evidemment, les fonctions en escalier sont intégrables, et leur intégrale comme fonctions en escalier est identique à leur intégrale comme fonctions intégrables ! Les fonctions intégrables sont en fait obtenues par un procédé de complétion de l’ensemble des fonctions en escalier, analogue à celui utilisé pour construire les nombres réels à partir des nombres rationnels…

3.3.L’intégration des fonctions continues

L’intégrale ainsi définie possède de nombreuses propriétés essentielles à la théorie des fonctions usuelles, et on peut caractériser très précisément, c’est-à-dire déterminer exactement, quelles sont les fonctions ainsi intégrables au sens de Riemann. En particulier, les fonctions monotones (croissantes ou décroissantes) sur un segment sont toujours intégrables au sens de Riemann, et on démontre aussi :

Théorème 1
Tout fonction numérique $f:[a,b]\to \mathbb R$ définie sur un segment réel et continue (par morceaux) est intégrable au sens de Riemann.

Une fonction continue par morceaux est une fonction continue sur les intervalles ouverts définis par une subdivision : il est clair que ce procédé d’intégration ne dépend pas du comportement des fonctions en un nombre fini de points. Ce théorème permet en tous cas de répondre à la question essentielle posée au début de cet article dans le cadre d’une fonction continue. En reprenant l’heuristique de la section 2, on choisit un point $x_0\in [a,b]$ : la restriction de la fonction $f$ à un segment inclus dans $[a,b]$ est continue également, donc intégrable, et on définit une fonction $F$ sur $[a,b]$ en posant $F(x)=\int_{x_0}^x f(t)\ dt$ pour tout $x\in [a,b]$ : ici la borne supérieure de l’intégrale est variable. On a alors :

Théorème 2
Si $f:[a,b]\to \mathbb R$ est une fonction continue, alors pour tout $x_0\in [a,b]$ la fonction $F:x\in [a,b]\mapsto \int_{x_0}^x f(t)\ dt$ est une primitive de $f$, autrement dit $F$ est dérivable et on a $F'(x)=f(x)$ pour tout $x\in [a,b]$.

Ce théorème est parfois appelé « théorème fondamental de l’analyse », puisqu’il relie les deux opérations fondamentales de l’analyse, la dérivation et l’intégration. Toutefois, une telle appellation désigne aussi parfois un autre théorème, lié à une notion plus puissante d’intégrale, dite « de Kurzweil-Henstock », qui généralise l’intégrale de Riemann. Mais ceci est une autre histoire !