Comme dans le plan euclidien $\mathbb R^2$ , il existe dans l’espace euclidien $\mathbb R^3$ une infinité de bases ou « systèmes de représentation » des vecteurs : l’espace étant intuitivement de dimension 3, ces bases sont toujours formées de 3 vecteurs non nuls. La décomposition d’un vecteur dans une base correspond à la résolution d’un système linéaire de 3 équations, et on peut donner une interprétation géométrique naturelle d’une telle décomposition.

1.Bases de l’espace euclidien

1.1.Du plan à l’espace euclidien : la base canonique

Nous avons défini les bases du plan euclidien $\mathbb R^2$ comme systèmes de représentation des vecteurs du plan. Rappelons que la base dite canonique est la base naturelle formée du couple $(\vec i,\vec j)$ (dans cet ordre), où $\vec i=(1,0)$ et $\vec j=(0,1)$ sont les vecteurs qui permettent de décomposer n’importe quel vecteur $\vec u=(x,y)$ du plan directement à partir de ses coordonnées naturelles $x$ et $y$, et dans l’ordre, c’est-à-dire sous la forme $\vec u=(x,y)=x.\vec i+y.\vec j$. Les bases canoniques existent dans tout espace réel naturel de dimension finie (c’est-à-dire de la forme $\mathbb R^n)$, et les bases en général dans tout espace vectoriel réel. Il est donc possible d’étendre ces concepts d’abord à l’espace euclidien $\mathbb R^3$.

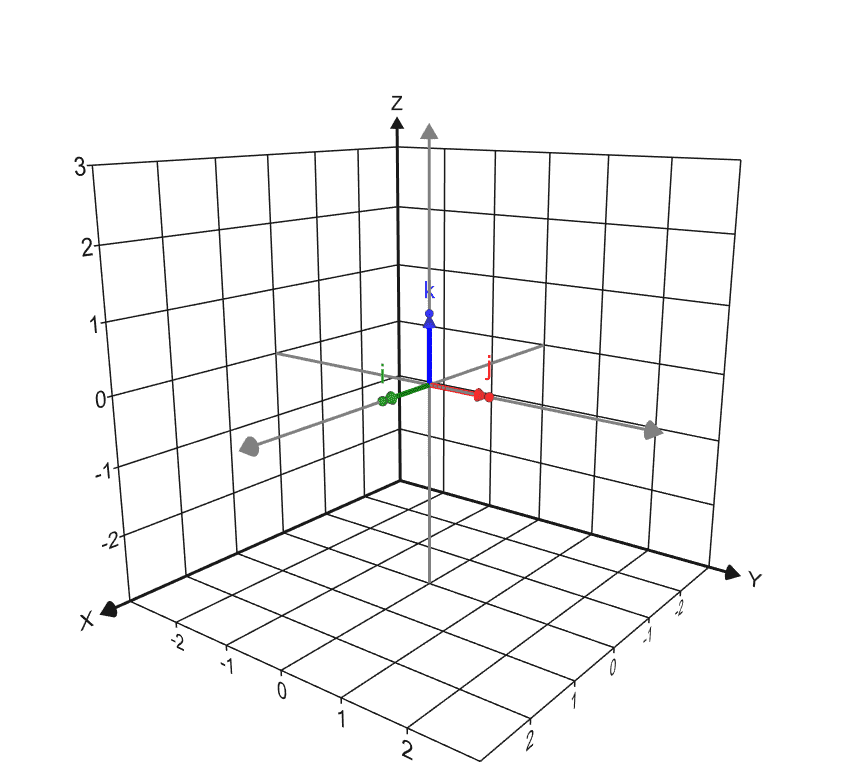
Par analogie avec le cas du plan, la base canonique de l’espace euclidien est le triplet de vecteurs $C=(\vec i,\vec j,\vec k)$, dans cet ordre, avec $\vec i=(1,0,0)$ , $\vec j=(0,1,0)$ et $\vec k=(0,0,1)$. Ces vecteurs permettent ici aussi de décomposer naturellement tout vecteur $\vec u=(x,y,z)$ de l’espace directement en fonction de ses coordonnées $x,y$ et $z$, et dans cet ordre, puisque l’on peut écrire, par définition de la multiplication d’un vecteur par un nombre réel : $$\vec u=x.(1,0,0)+y.(0,1,0)+z.(0,0,1)=x.\vec i+y.\vec j+z.\vec k.$$ On dit que les coordonnées de $\vec u$ dans la base $C$ sont $(x,y,z)$ : la base est dite « canonique » parce que le système de coordonnées est identique au vecteur de l’espace (voir la figure 2 pour une interprétation géométrique de ces coordonnées).

1.2.Autres bases de l’espace euclidien

Comme dans le plan, il existe d’autres bases de l’espace, en fait une infinité, comme dans le plan parce que l’ensemble $\mathbb R$ est infini. Par exemple, en changeant l’ordre des vecteurs $\vec i,\vec j$ et $\vec k$ de la base canonique, on obtient d’autres bases : $C_1=(\vec j,\vec k,\vec i)$, $C_2=(\vec k,\vec i,\vec j)$ (obtenues par permutations circulaires de $C$), $C_3=(\vec i,\vec k,\vec j)$ (obtenue par échange de $\vec j$ et $\vec k$), $C_4=(\vec k,\vec j,\vec i)$ et $C_5=(\vec j,\vec i,\vec k)$ (obtenues par permutations circulaires de $C_3$). Ces 6 bases sont toutes celles qu’on peut obtenir avec ces trois vecteurs; par exemple, pour un vecteur $\vec u=(x,y,z)$ de $\mathbb R^3$ on a $\vec u=y.\vec j+x.\vec i+z.\vec k$, donc les coordonnées de $\vec u$ dans la base $C_5$ sont données par le triplet $(y,x,z)$ : elles sont donc différentes des coordonnées $(x,y,z)$ du même vecteur dans la base $B$, puisque l’ordre change !

Définition 1
En général, l’espace euclidien $\mathbb R^3$ étant intuitivement « de dimension $3$ », une base est la donnée d’un triplet $(\vec u_1,\vec u_2,\vec u_3)$ de vecteurs (et pas de nombres réels !), possédant les propriétés suivantes :
i) Si $a,b,c$ sont trois nombres réels tels que $a.\vec u_1+b.\vec u_2+c.\vec u_3=\vec 0$, alors $a=b=c=0$ (on dit que les vecteurs $\vec u_1$, $\vec u_2$ et $\vec u_3$ sont linéairement indépendants)
ii) Si $\vec v$ est un vecteur de l’espace, alors il existe des nombres réels $a,b,c$ tels que $\vec v=a.\vec u_1+b.\vec u_2+c.\vec u_3$ (on dit que les vecteurs $\vec u_1$, $\vec u_2$ et $\vec u_3$ engendrent l’espace).

1.3.Propriétés essentielles d’une base

Rappelons que pour un vecteur $\vec v=(x,y,z)$, sa multiplication $a.\vec v$ par un nombre réel $a$ se fait coordonnée par coordonnée, de sorte que $a.\vec v=(a.x,a.y,a.z)$. La condition (ii) de la définition 1 exprime bien l’idée d’un « système de représentation » : tout vecteur de l’espace de « représente » à partir des vecteurs $\vec u_1$, $\vec u_2$ et $\vec u_3$. La condition (i) de la définition assure qu’une telle représentation est unique, de sorte que l’unique triplet de nombres réels $(a,b,c)$ décrivant $\vec v$ sous la forme $a.\vec u_1+b.\vec u_2+c.\vec u_3$ (ce qu’on appelle une combinaison linéaire de ces vecteurs) sont les coordonnées du vecteur $\vec v$ dans la base $(\vec u_1,\vec u_2,\vec u_3)$. Cette première condition énonce en fait, sous une forme mathématiquement plus commode, l’idée intuitive que les trois vecteurs $\vec u_1$, $\vec u_2$ et $\vec u_3$ « pointent dans des directions différentes » : comme ils déterminent ainsi 3 directions d’un espace à 3 dimensions, ils permettent de « quadriller » tout l’espace. On peut en fait démontrer qu’ici les conditions (i) et (ii) sont équivalentes, et donc redondantes.

En somme, une base de l’espace euclidien est un triplet $B$ de vecteurs par rapport auquel tout vecteur $\vec v$ de l’espace possède une (unique) représentation à l’aide d’une combinaison linéaire, dont les coefficients sont par définition les coordonnées de $\vec v$ dans la base $B$.

Exemple 1
i) Les vecteurs $\vec u_1=(0,-2,1)$ et $\vec u_2=(0,6,-3)$ sont proportionnels, puisque $\vec u_2=3.\vec u_1$ : pour tout vecteur $\vec u_3=(x,y,z)$, on peut alors écrire $3.\vec u_1+(-1).\vec u_2+0.\vec u_3=(0,0,0)=\vec 0$, donc les vecteurs $\vec u_1$, $\vec u_2$ et $\vec u_3$ ne sont pas linéairement indépendants : ils ne peuvent pas former une base.
ii) Soient $\vec u_1=(0,-2,1)$, $\vec u_2=(5,0,-3)$ et $\vec u_3=(1,-1,1)$ : si $a,b,c$ sont des nombres réels tels que $a.\vec u_1+b.\vec u_2+c.\vec u_3=(0,0,0)$, alors coordonnée par coordonnée on a $5b+c=0$, $-2a-c=0$ et $a-3b+c=0$, d’où $c=-2a=-5b$ (à partir des deux premières équations), d’où $a=-c/2$ et $b=-c/5$, et finalement $-c/2+3c/5+c=0$ (en remplaçant dans la dernière équation), c’est-à-dire $11c/10=0$, et donc $c=0=a=b$ : le triplet $(\vec u_1,\vec u_2,\vec u_3)$ est une base de l’espace euclidien.

2.Décomposition d’un vecteur dans une base

2.1.A partir de la résolution d’un système d’équations

Etant donnés une base $B=(\vec u_1,\vec u_2,\vec u_3)$ de l’espace et un vecteur $\vec v=(x,y,z)$ quelconque, comment décomposer le vecteur $\vec v$ dans la base $B$ ? On doit, comme dans le plan, résoudre un système, ici un système de trois équations à trois inconnues, dont on sait qu’il possède une unique solution, précisément parce que $B$ est une base. Pour écrire ce système de manière générique, introduisons des coordonnées pour les vecteurs de la base $B$ : nous écrirons $\vec u_1=(x_1,y_1,z_1)$, $\vec u_2=(x_2,y_2,z_2)$ et $\vec u_3=(x_3,y_3,z_3)$. Nous cherchons donc des nombres réels $a,b,c$ tels que $(x,y,z)=\vec v=a.\vec u_1+b.\vec u_2+c.\vec u_3=(ax_1+bx_2+cx_3,ay_1+by_2+cy_3,az_1+bz_2+cz_3)$, c’est-à-dire, coordonnée par coordonnée, tels que les trois équations suivantes soient simultanément vérifiées :

$$\left\{\begin{eqnarray} x &=& ax_1+bx_2+cx_3\\y &=& ay_1+by_2+cy_3\\z &=& az_1+bz_2+cz_3.\end{eqnarray}\right.$$

La résolution générale d’un tel système est toujours possible, même si elle nécessite par commodité l’introduction de concepts d’algèbre linéaire comme les matrices de taille 3 et leurs déterminants. Le résultat est alors donné sous la forme de formules explicites exprimant les coefficients cherchés $a,b,c$ en fonction des coordonnées de $\vec u_1$,$\vec u_2$ et $\vec u_3$, et des coordonnées $x,y,z$ du vecteur $\vec v$.

Exemple 2
Avec la base $B$ de l’exemple 1 (ii), on doit résoudre le système suivant : $$\left\{\begin{eqnarray} x &=& 5b+c\\y &=& -2a-c\\z &=& a-3b+c.\end{eqnarray}\right.$$
La première équation nous donne $c=x-5b$, d’où en remplaçant dans la deuxième et la troisième, $y=-2a-x+5b$ et $z=a-3b+x-5b$ : en additionnant celles-ci, on obtient $y+z=-a-3b$. Des deux premières équations on tire également $x+y=5b-2a$, d’où $(x+y)-2(y+z)=11b$, ce qui nous donne $b=(1/11)(x-y-2z)$, et finalement $a=-y-z-3b=(1/11)(-3x-8y-5z)$ et $c=x-5b=(1/11)(6x+5y+10z)$. Les coordonnées de $\vec v=(x,y,z)$ dans la base $B$ dont donc $(a,b,c)$, avec les valeurs calculées; le coefficient $1/11$ qui apparaît à chaque fois est l’inverse du « déterminant du système ».

2.2.Interprétation géométrique de la décomposition