Dans la géométrie intuitive on définit les aires des figures sans justification ou sans démonstration. Dans la géométrie euclidienne moderne, c’est-à-dire analytique, la définition de l’aire du triangle et du parallélogramme se fondent sur des définitions univoques de celles du triangle rectangle et du rectangle. Mais ces définitions recèlent des ambiguïtés, qu’il est possible de lever à l’aide de rudiments de trigonométrie.

1.Définir l’aire d’un triangle quelconque

1.1.Définir l’aire d’un triangle à partir d’une hauteur

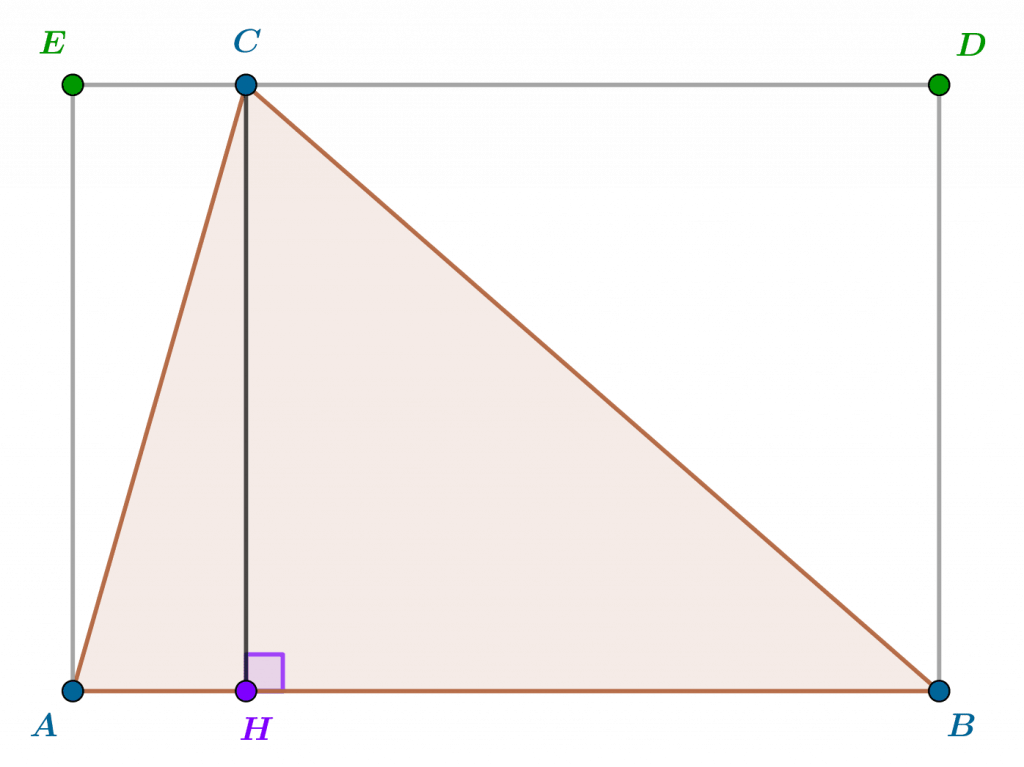
Si $ABC$ est un triangle rectangle en $B$, l’intuition nous suggère de définir son aire comme la moitié de l’aire du rectangle formé à partir de $ABC$, autrement dit simplement comme $(1/2).AB.AC$. En général, si $ABC$ est un triangle quelconque, on peut alors envisager définir l’aire de $ABC$ en le découpant en deux triangles rectangles, dont on additionnerait les aires définies comme précédemment, en menant donc une hauteur par l’un des sommets d’angle aigu du triangle. Par exemple si l’angle $\widehat A$ est aigu, on mène en $H$, point du segment $[AB]$, la hauteur passant par $C$ (voir la figure n°1). On définirait alors naturellement l’aire du triangle $ABC$ comme la somme des aires des triangles respectifs $AHC$ (rectangle en $H$) et $BHC$ (rectangle en $H$ aussi), soit $(1/2).AH.HC+(1/2).HB.HC=(1/2).(AH+HB).HC=(1/2).AB.HC$. Pour qu’une telle définition soit valable pour n’importe quel triangle, elle devrait cependant ne pas dépendre du choix d’un angle du triangle, et nous devons donc surmonter deux problèmes :

Problème n°1
La définition présente est modelée sur le calcul d’une grandeur définie a priori à partir d’un angle aigu, et il n’est pas clair a priori qu’elle demeure valable pour le choix d’un angle obtus.

Problème n°2
La définition présente dépend du choix de l’un des sommets d’angle aigu du triangle, et donc est a priori ambiguë : pourquoi n’obtiendrait-on pas un résultat différent à partir d’un autre choix ?

En montrant d’abord que le problème n°1 n’en est pas vraiment un, nous pourrons ensuite résoudre le problème n°2 sans hypothèse particulière, grâce à un peu de trigonométrie élémentaire.

1.2.Définir l’aire d’un triangle obtusangle

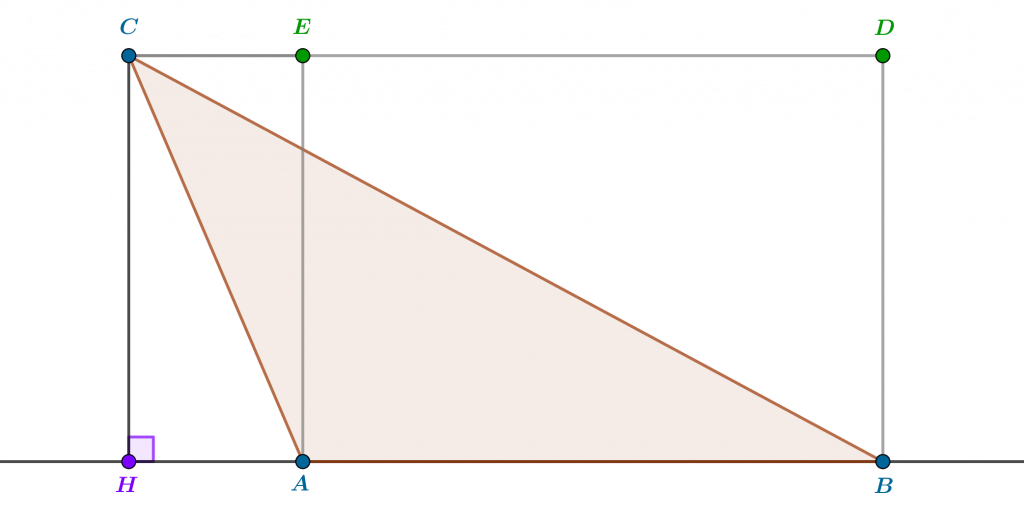
Supposons que $ABC$ est un triangle obtusangle, possédant donc un angle obtus, par exemple l’angle $\widehat A$, et menons comme précédemment par le point $H$ de la droite $(AB)$ la hauteur du triangle issue de $C$ (voir la figure). Dans cette configuration où le point $H$ n’est en général pas sur le segment $[AB]$, l’intuition nous suggère de définir plutôt l’aire de $ABC$, cette fois-ci comme la différence des aires des triangles $BHC$ et $AHC$, rectangles en $H$, c’est-à-dire $(1/2).(BH.HC)-(1/2).(AH.HC)=(1/2).(BH-AH).HC$ en factorisant. Mais, précisément parce que dans cette configuration l’angle $\widehat A$ est obtus, la différence $BH-AH$ est à nouveau la longueur $AB$, là où celle-ci vaut $BH+AH$ lorsque l’angle $\widehat A$ est aigu. Ainsi, nous aboutissons dans tous les cas à la même formule pour la définition de l’aire du triangle $ABC$, soit $(1/2)AB.HC$. Il reste à montrer que cette définition ne dépend pas du sommet par lequel on mène la hauteur dont la longueur sert à la définition.

1.3.Vérification trigonométrique de la définition

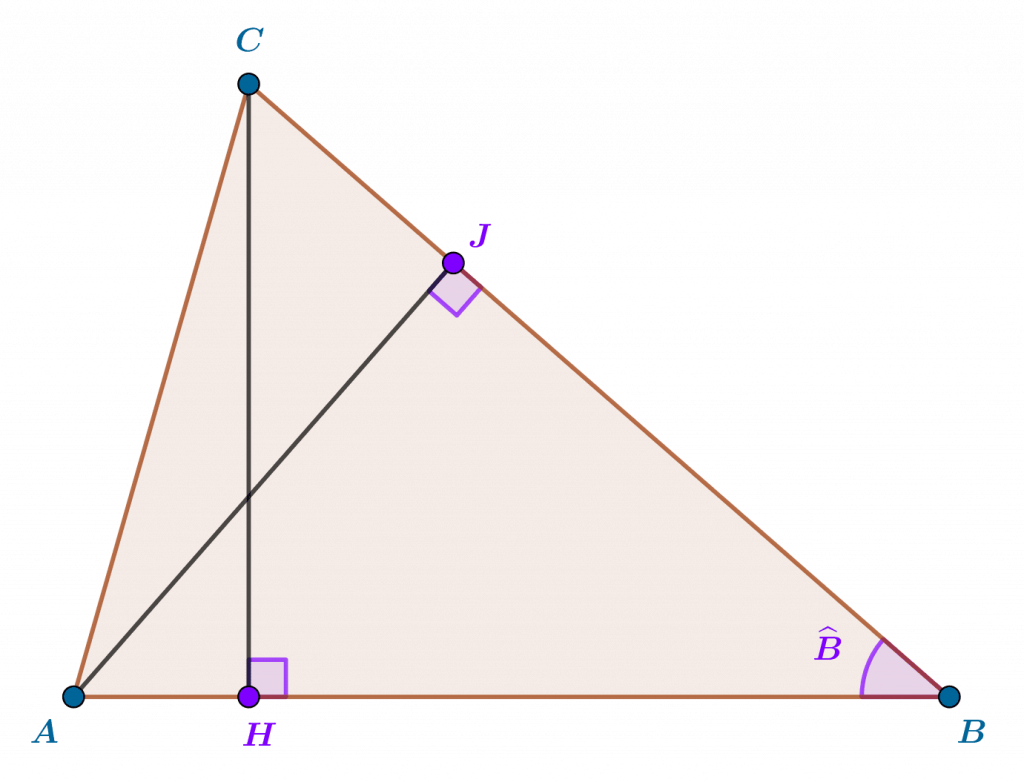
Ayant résolu le problème n°1, nous pouvons désormais travailler à partir d’un triangle $ABC$ quelconque, en supposant ici qu’il n’est pas dégénéré (c’est-à-dire plat) : le cas du triangle plat ne présente pas de difficulté, son aire est par définition nulle. Or, puisqu’il n’est pas nécessaire de distinguer angles aigus et angles obtus, les angles et côtés du triangle $ABC$ jouent désormais un rôle symétrique : ils sont interchangeables dans les raisonnements. Cela signifie que pour vérifier notre définition du triangle, il suffit de montrer qu’elle aboutit au même résultat lorsqu’on choisit deux côtés différents de $ABC$, par exemple $[AB]$ et $[BC]$. En conservant les mêmes notations ajoutons un point $J$ sur la droite $(BC)$, de sorte que la droite $(JA)$ soit la hauteur de $ABC$ issue de $A$ (voir la figure n°3) : $[AB]$ est l’hypoténuse du triangle $AJB$ rectangle en $J$, $[BC]$ celle du triangle $BHC$ rectangle en $H$. Par caractérisation élémentaire du sinus de l’angle $\widehat B$ dans ces deux triangles rectangles, on a alors $AJ/AB=HC/BC$ d’où $AJ.BC=HC.AB$. Or, on reconnaît aux deux membres de cette équation les deux manières de calculer (le double) de l’aire de $ABC$, en partant soit du côté $[BC]$, soit du côté $[AB]$ : la définition de l’aire ne dépend pas du choix d’un des côtés, et nous avons résolu le problème n°2. Nous pouvons donc définir désormais en général, sans ambiguïté, l’aire d’un triangle $ABC$ de la manière suivante :

Proposition
Soit $ABC$ est un triangle non dégénéré quelconque, et soient :
i) $H$ l’intersection de la droite $(AB)$ avec la hauteur de $ABC$ issue de $C$
ii) $I$ l’intersection de la droite $(AC)$ avec la hauteur de $ABC$ issue de $B$
iii) $J$ l’intersection de la droite $(BC)$ avec la hauteur de $ABC$ issue de $A$.
Alors, on a les égalités $(1/2).AB.HC=(1/2).AC.IB=(1/2).BC.JA$, et ce nombre réel est par définition l’aire du triangle $ABC$.

2.Bien définir l’aire d’un parallélogramme

2.1.Définition de l’aire du parallélogramme

Les deux membres de l’équation précédente ($AJ.BC=HC.AB$) font apparaître le double de l’aire $(1/2).AB.HC$ du triangle $ABC$ : on peut alors naturellement interpréter la quantité $AB.HC$ comme l’aire du parallélogramme $ABDC$ obtenu en symétrisant le triangle $ABC$ par rapport au côté $[BC]$ ($D$ est le symétrique de $A$ par rapport au milieu de $[BC]$). En effet, la symétrie préserve les distances, si bien que l’aire du triangle symétrique $BCD$ est égale à celle de $ABC$, et il suffit alors d’ajouter les deux pour obtenir une définition de l’aire du parallélogramme. Cette formule possède une signification intuitive évidente, qui nous sert ici à définir directement l’aire d’un parallélogramme $ABDC$ quelconque (voir la figure n°4) : ce devrait être l’aire du rectangle $ABKE$, où $H$ est le point de $(AB)$ tel que $(HD)$ est la hauteur du triangle $ABD$ issue de $D$, et $K$ le point de $(CD)$ tel que $(KH)$ est la hauteur du triangle $BCD$ issue de $B$. Intuitivement, cette aire est le produit $AB.AE$, soit $AB.HD$, double de l’aire du triangle $ABD$.

2.2.Additivité des aires des triangles