Introduction

Dans Produit scalaire et loi des cosinus, nous avons montré à partir des angles orientés comment l’interprétation trigonométrique du produit scalaire de deux vecteurs conduisait à une généralisation du théorème de Pythagore, la « loi des cosinus » ou théorème d’Al-Kashi, qui met en relation la longueur des côtés et le cosinus des angles d’un triangle. La « loi des sinus » est une relation qui, par analogie met en relation les longueurs des côtés et les sinus des angles; à partir du calcul de base de l’aire du triangle utilisant la hauteur, on en tire, grâce à la loi des cosinus, la formule de Héron, qui fournit l’aire du triangle en fonction de la seule longueur de ses côtés.

1.La loi des sinus

Tout comme la loi des cosinus relie les cosinus des angles d’un triangle aux longueurs des côtés de ce triangle, la loi des sinus, simple reformulation de relations trigonométriques élémentaires, relie les sinus des angles aux longueurs des côtés. En voici l’énoncé :

Loi des sinus
Si $ABC$ est un triangle plan non dégénéré, de côtés $a=BC$, $b=AC$ et $c=AB$, et d’angles $\alpha=\widehat{BAC}$, $\beta=\widehat{ABC}$ et $\gamma=\widehat{ACB}$, alors on a $a/\sin\alpha=b/\sin\beta=c/\sin\gamma$.

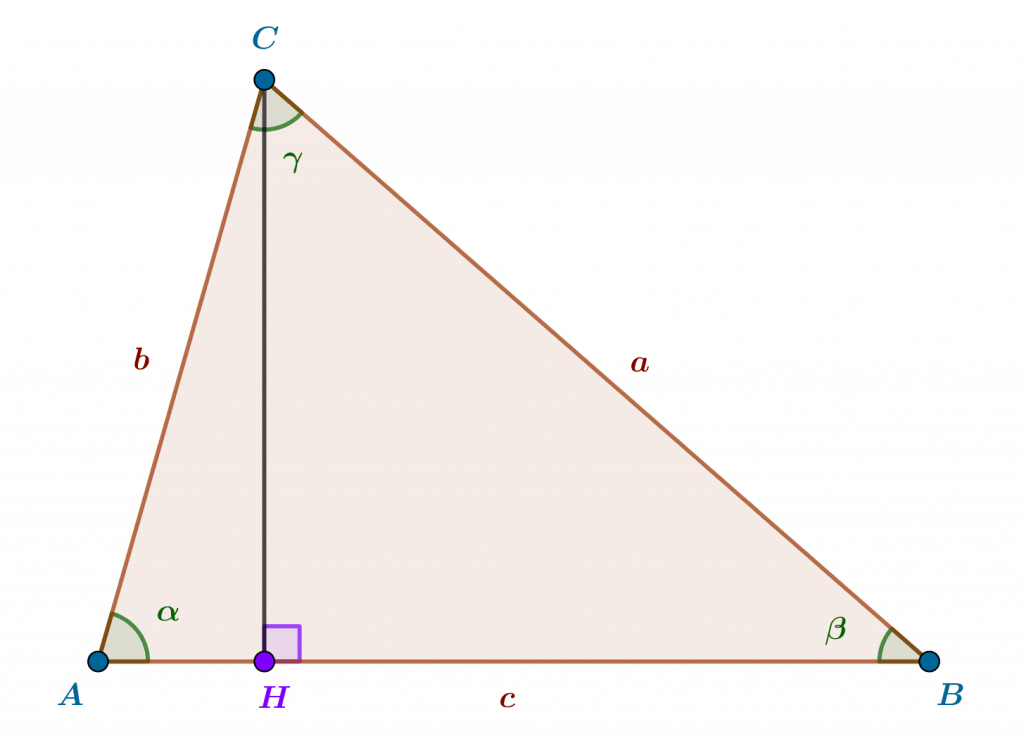
La démonstration de ces égalités est simple. Par exemple, en menant par le point $H$ de la droite $(AB)$ la hauteur du triangle $ABC$ passant par $C$, on obtient deux triangles $ACH$ et $ABH$, rectangles en $H$. Par les propriétés trigonométriques élémentaires du triangle rectangle, on a alors $\sin\alpha=HC/AC$ et $\sin\beta=HC/BC$, ou encore $HC=AC.\sin\alpha=b\sin\alpha$ et $HC=BC.\sin\beta=a\sin\beta$, de sorte que $a\sin\beta=b\sin\alpha$, ou encore $a/\sin\alpha=b/\sin\beta$ (on peut diviser par ces sinus, non nuls puisque le triangle n’est pas dégénéré). En menant la hauteur de $ABC$ par l’un des deux autres sommets $A$ ou $B$, par analogie on trouve la seconde égalité.

2.Expression trigonométrique de l’aire du triangle

Dans la démonstration précédente, nous avons utilisé la construction d’une hauteur issue de l’un des sommets du triangle, que nous avons déjà invoquée pour définir l’aire du triangle dans Définir l’aire du triangle et du parallélogramme. Rappelons, avec les mêmes notations que précédemment, que l’aire du triangle $ABC$ est alors $(1/2).AB.HC$, soit la moitié de l’aire $AB.HC$ du parallélogramme construit sur les vecteurs $\vec{AB}$ et $\vec{AC}$. Les relations précédentes permettent de reformuler ce calcul à partir du sinus de l’un des angles :

Théorème 1
L’aire du triangle $ABC$ est $(1/2)ab\sin\gamma=(1/2)ac\sin\beta=(1/2)bc\sin\alpha$.

En effet, dans le triangle $AHC$ rectangle en $H$, on a $HC=b\sin\alpha$, donc $bc\sin\alpha=AB.HC$, d’où le résultat. Le choix d’une autre hauteur donne un calcul analogue réalisé avec un autre angle, et on sait que le calcul de l’aire ne dépend pas de ce choix (ibid.). Nous sommes donc passés d’un calcul de l’aire du triangle mentionnant explicitement l’une des hauteurs, à un calcul ne faisant intervenir que le sinus d’un des angles et la longueur des deux côtés de cet angle.

3.La formule de Héron