par Jean Barbet | Avr 30, 2024 | Analyse, Ensembles, Nombres
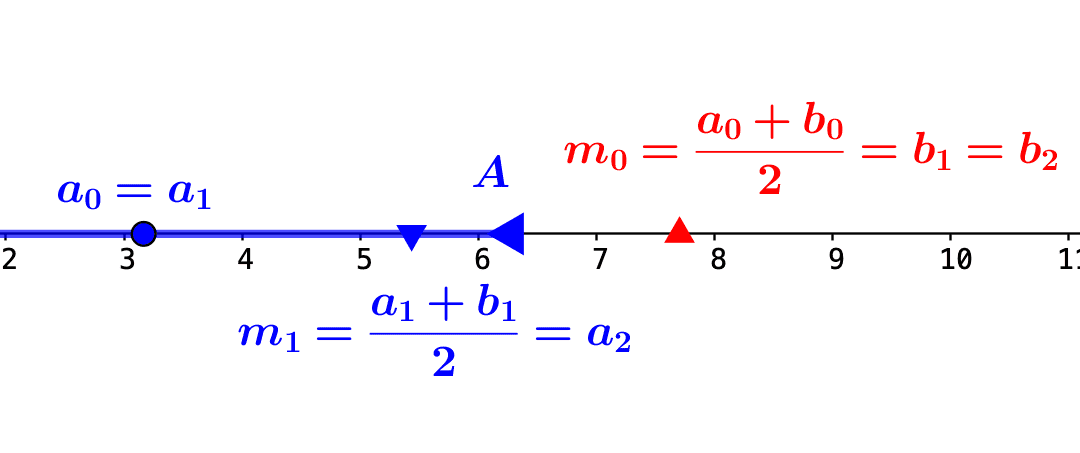
L’ensemble des nombres réels, quelle que soit la manière dont il est présenté, défini ou construit, n’est pas une multiplicité « amorphe », mais il vient avec une « structure » naturelle, héritée en dernière analyse de la structure arithmétique de...
par Jean Barbet | Mar 27, 2024 | Algèbre, Nombres
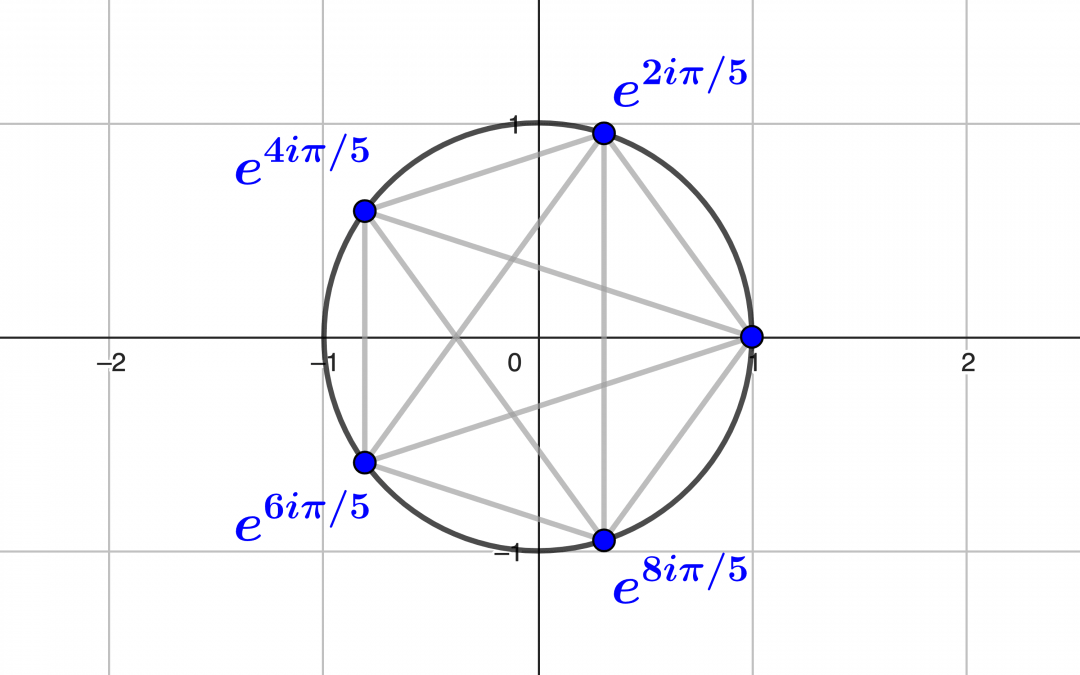
Les propriétés des polynômes à une indéterminée sur un corps sont analogues à celles des nombres entiers relatifs. En exploitant cette analogie à partir de la notion de polynôme irréductible, on en tirer des informations précieuses sur l’arithmétique des...

par Jean Barbet | Mar 7, 2024 | Algèbre, Ensembles, Fonctions, Nombres
Les fractions rationnelles à une indéterminée apparaissent à la convergence de la théorie des fonctions rationnelles et de la théorie des polynômes. En généralisant la construction des nombres rationnels à partir des nombres entiers relatifs, on les construit comme...
par Jean Barbet | Jan 19, 2024 | Algèbre, Géométrie, Nombres
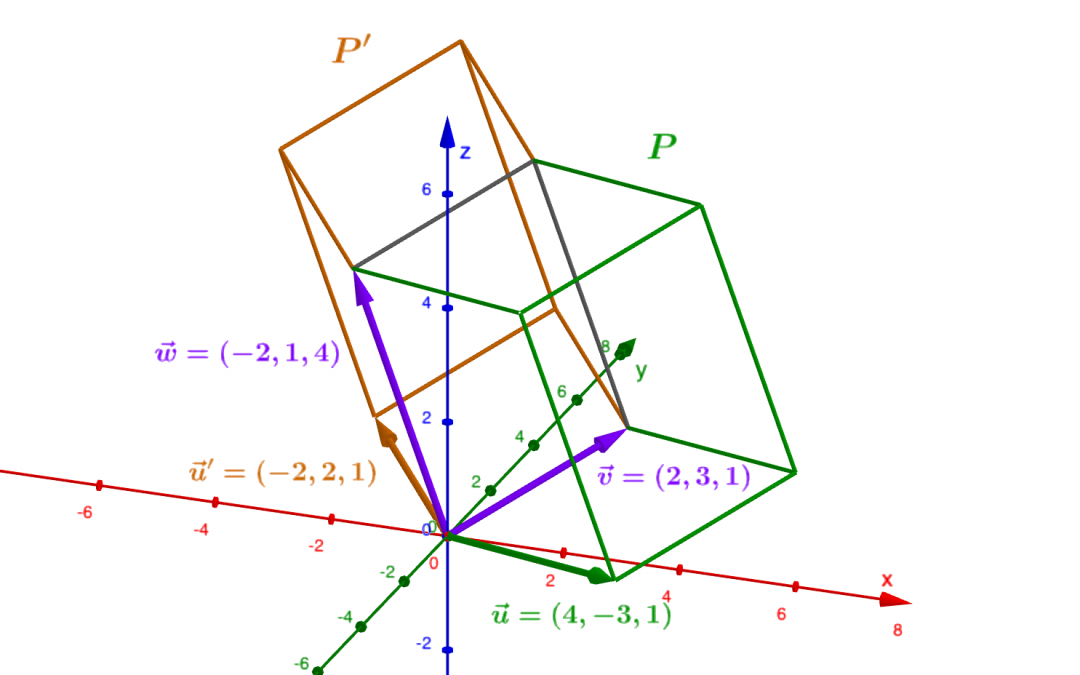
Le plan euclidien acquiert une orientation naturelle par le choix d’une base, que l’on peut qualifier de directe ou d’indirecte. Cette orientation se manifeste à travers le signe du déterminant de la base, correspondant à l’aire algébrique du...

par Jean Barbet | Oct 10, 2023 | Ensembles, Nombres
Quand il s’agit de compter ou de classer des ensembles, nous faisons appel à deux types de nombres : les ordinaux et les cardinaux. Alors que les nombres ordinaux nous aident à mettre en ordre une série d’éléments (premier, deuxième, troisième, etc.), les...
par Jean Barbet | Sep 25, 2023 | Ensembles, Nombres
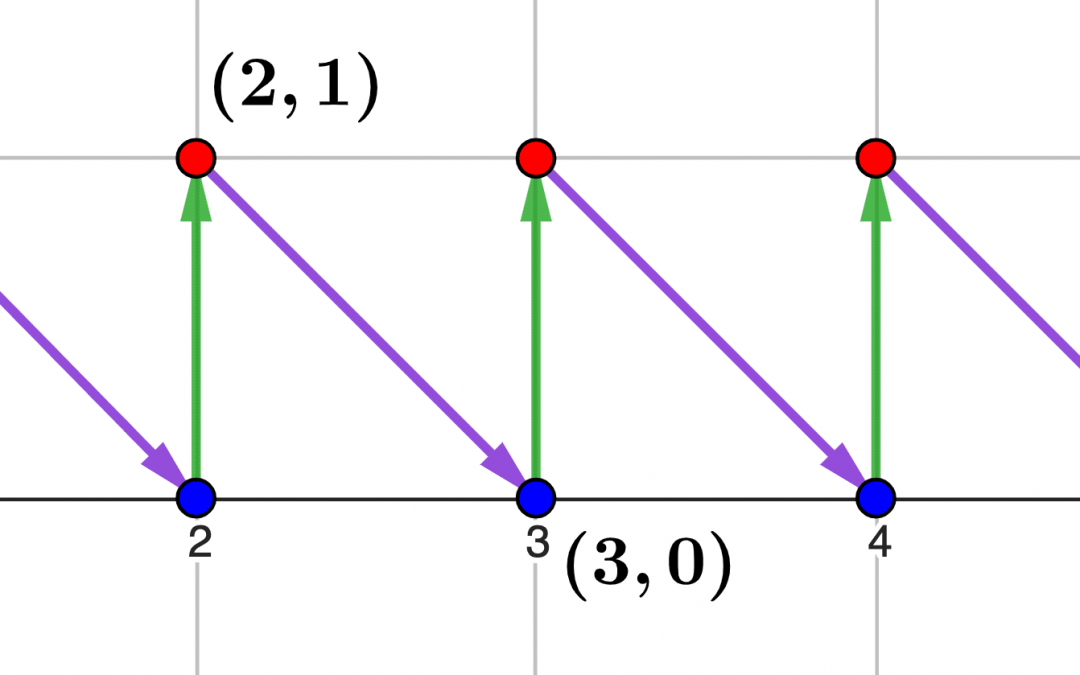
Les nombres entiers naturels ont deux visages : d’un côté, ils peuvent être vus comme des séquences ou des « énumérations » – ce qu’on appelle les nombres ordinaux. De l’autre, ils sont perçus comme des « quantités », ce qui nous mène aux nombres...







