Le plan euclidien acquiert une orientation naturelle par le choix d’une base, que l’on peut qualifier de directe ou d’indirecte. Cette orientation se manifeste à travers le signe du déterminant de la base, correspondant à l’aire algébrique du parallélogramme orienté formé par les deux vecteurs de la base. De manière analogue, l’orientation de l’espace euclidien peut être définie : en considérant le volume algébrique d’un parallélépipède orienté défini par une base de l’espace, on parvient à une généralisation spatiale du concept de déterminant. Cette généralisation permet alors de distinguer un sens direct et un sens indirect dans l’espace tridimensionnel.

1.Orienter l’espace euclidien

1.1.Partir de l’orientation du plan ?

Comme le plan euclidien, représenté par l’ensemble $\mathbb R^2$ des couples $(x,y)$ de nombres réels, l’espace euclidien peut être orienté. Dans le plan, l’orientation repose sur une intuition assez directe : le « sens de rotation » d’un vecteur unitaire à un autre vecteur unitaire. Autrement dit, une orientation du plan est fixée par la donnée d’une base, c’est-à-dire d’un couple $(u,v)$ de vecteurs non nuls et non colinéaires, et l’orientation « standard », dite directe, est donnée par la base canonique $(i,j)$, où $i=(1,0)$ et $j=(0,1)$ sont les vecteurs qui permettent de décomposer naturellement tout vecteur du plan $(x,y)$ en ses coordonnées naturelles sous la forme $(x,y)=x.i+y.j$. Il n’existe alors le plan que deux orientations possibles : le sens direct (celui de la base canonique) et le sens indirect (celui de la base $(j,i)$, opposée de la base canonique).

1.2.La convention géométrique des physiciens

Dans l’espace euclidien, représenté par l’ensemble $\mathbb R^3$ des triplets $(x,y,z)$ de nombres réels, l’intuition de l’orientation n’est pas aussi directe, mais la théorie de l’orientation du plan s’y prolonge de manière féconde, comme dans tous les espaces réels de dimension finie. Les physiciens utilisent à titre de représentation géométrique la règle dite du « tire-bouchon » ou du « bonhomme d’Ampère » : si les trois premiers doigts de la main droite représentent des vecteurs $u_1,u_2,u_3$ linéairement indépendants – c’est-à-dire formant une base de $\mathbb R^3$ (voir Bases de l’espace euclidien)- on considère que la base $(u_1,u_2,u_3)$ définit une orientation directe. Comme on se représente en général la base canonique $(i,j,k)$ de l’espace euclidien – avec $i=(1,0,0)$, $j=(0,1,0)$ et $k=(0,0,1)$ – comme orientée dans le sens direct, cette règle permet de retrouver visuellement cette convention, qui mathématiquement doit toutefois être justifiée par une extension de la théorie du plan.

2.Le déterminant

2.1.L’orientation du plan est définie par le déterminant

En effet, dans le plan le caractère direct de l’orientation de la base canonique $(i,j)$ n’est pas qu’une convention reposant sur la décomposition naturelle des vecteurs : il se fonde sur l’interprétation algébrique de l’orientation d’une base $(u,v)$ – avec $u=(a,b)$ et $v=(c,d)$ – comme le signe du déterminant $det(u,v)=ad-bc$ (jamais nul) de celle-ci. Si $det(u,v)>0$, par définition la base est directe, tandis que si $det(u,v)<0$, par définition la base est indirecte : ainsi, la base canonique est directe puisque $det(i,j)=1.1-0.0=1>0$, et il n’y a que deux orientations possibles parce que les nombres réels non nuls ne peuvent avoir que deux signes différents… Pour étendre cette théorie algébrique à l’espace euclidien, il nous faudrait définir le déterminant de trois vecteurs de l’espace, et vérifier qu’il est non nul si et seulement si les vecteurs forment une base. Nous pourrons alors définir l’orientation d’une base comme le signe de son déterminant !

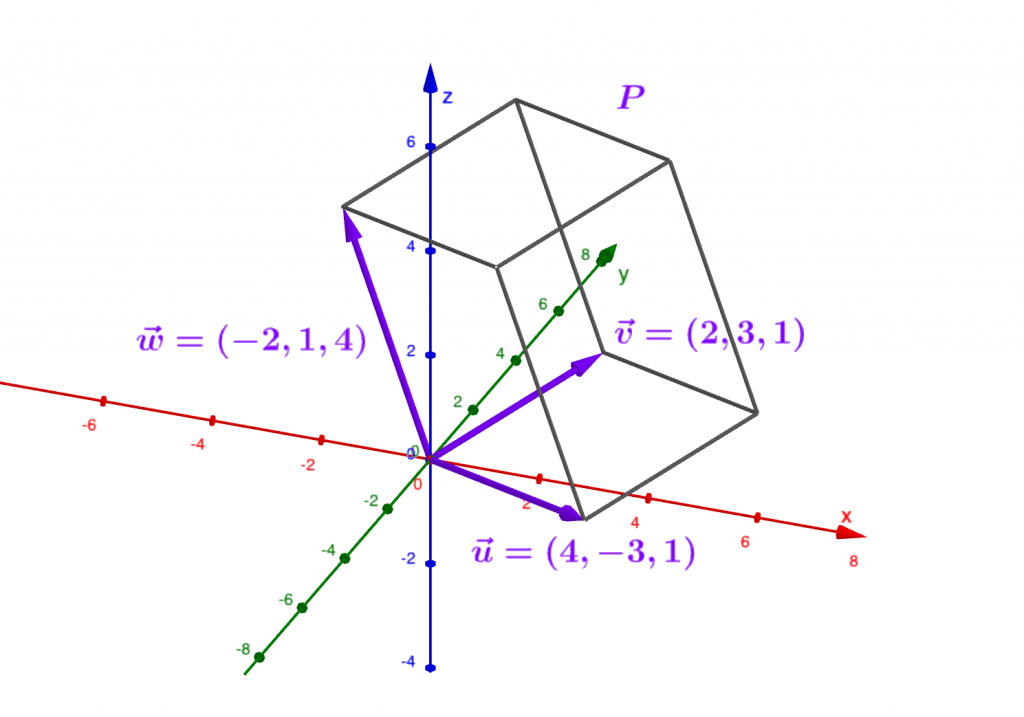
2.2.De l’aire du parallélogramme au volume du parallélépipède

Le déterminant de trois vecteurs $u,v,w$ de l’espace euclidien est aussi appelé produit mixte de ces trois vecteurs, et peut être défini à partir d’une généralisation spatiale de la caractérisation du déterminant de deux vecteurs du plan comme aire algébrique du parallélogramme qu’ils déterminent (voir L’interprétation géométrique plane du déterminant). Ainsi, plutôt que d’introduire une définition dépourvue de sens ou de justification, nous allons nous appuyer sur cette interprétation géométrique du déterminant dans le plan, pour en induire sa définition analytique dans l’espace. La généralisation d’un parallélogramme à l’espace étant un parallélépipède, ceci signifie que nous devons donc définir le déterminant $det(u,v,w)$ comme le « volume algébrique » du parallélépipède (implicitement orienté !) que ces trois vecteurs déterminent dans cet ordre.

3.Le produit mixte

3.1.Heuristique d’une définition spatiale du déterminant

Donnons-nous trois vecteurs $u,v,w$ de l’espace $\mathbb R^3$, et considérons le parallélépipède $P$ qu’ils décrivent; donnons-nous également un autre vecteur $u’$, et le parallélépipède $P’$ déterminé par $u’,v,w$. Afin de définir le déterminant $det(u,v,w)$ de $u,v,w$ comme le « volume algébrique de $P$ », nous pouvons nous appuyer sur l’heuristique suivante, qui énumère les critères que doit satisfaire le déterminant comme fonction :
i) Si on multiplie l’un des vecteurs – soit la longueur d’un jeu d’arêtes parallèles de $P$ – par un coefficient $\lambda\in\mathbb R$, alors le volume algébrique doit être multiplié par $\lambda$
ii) Si on assemble les deux parallélépipèdes $P$ et $P’$ selon leurs deux arêtes communes $v,w$ en additionnant $u$ et $u’$, alors le volume algébrique du parallélépipède obtenu doit être la somme de ceux de $P$ et de $P’$
iii) Si deux des vecteurs sont égaux (si $P$ est contenu dans un plan), le volume algébrique doit être nul
iv) Si on change l’orientation des trois vecteurs, alors le volume algébrique doit changer de signe.

Ici il semblerait que nous tournions en rond : nous voulons définir l’orientation d’une base par son déterminant, lequel mentionne un critère d’orientation. Il faut donc remplacer le critère (iv) par un critère tiré de l’intuition du plan :
iv’) Si on échange deux vecteurs, le volume algébrique changer de signe.

En effet, le déterminant de deux vecteurs du plan change de signe si on les permute, et l’intuition géométrique du bonhomme d’Ampère suggère qu’en permutant deux vecteurs on change d’orientation dans l’espace.

3.2.Propriétés algébriques du déterminant

Ces quatre propriétés élémentaires suffisent à définir le déterminant ou produit mixte $[u,v,w]$ de trois vecteurs $u,v,w$ de l’espace, si l’on se donne pour convention, à nouveau, que le produit mixte des vecteurs $i,j,k$ de la base canonique est $1$. En effet, ces vecteurs forment un cube d’arête $1$ orienté dans le sens pris comme référence, puisqu’ils fournissent la décomposition naturell de tout vecteur $u=(x,y,z)$ sous la forme $u=x.i+y.j+z.k$. Les contraintes précédentes se traduisent alors, sur le plan algébrique, de la manière suivante pour tous vecteurs $u,v,w$ :
i) Le produit mixte doit être linéaire en chaque argument : pour tout $\lambda\in\mathbb R$ et tous vecteurs $u’,v,’,w’$, on doit avoir $[\lambda u+u’,v,w]=\lambda [u,v,w]+[u’,v,w]$, et de même pour les autres coordonnées $v$ et $w$, $[u,\lambda v+v’,w]=\lambda [u,v,w]+[u,v’,w]$ et $[u,v,\lambda w+w’]=\lambda [u,v,w]+[u,v,w’]$
ii) Si $u=v$, $u=w$ ou $v=w$, alors on doit avoir $[u,v,w]=0$
iii) Si on échange $u$ et $v$, $u$ et $w$, ou $v$ et $w$, le déterminant doit changer de signe : on a $[u,w,v]=[v,u,w]=[w,v,u]=-[u,v,w]$.

Notons que la linéarité est introduite ici en (i) comme combinaison de l’homogénéité (i) et de l’additivité (ii) du paragraphe précédent, et que (ii) est en fait une conséquence de (iii). Appliquons d’abord ces contraintes aux vecteurs de base $i,j,k$ avec la convention $[i,j,k]=1$. A partir de simples échanges de ces vecteurs (condition (iii)), nous sommes amenés à poser également :

• $[i,k,j]=-1$
• $[j,i,k]=-1$
• $[j,k,i]=1$
• $[k,i,j]=1$
• $[k,j,i]=-1$.

3.3.Définition analytique du produit mixte

Pour définir proprement le produit mixte, il nous suffit alors d’analyser par linéarité les conséquences des contraintes précédentes à partir des coordonnées de trois vecteurs $u_1=(a_{11},a_{12},a_{13})$, $u_2=(a_{21},a_{22},a_{23})$ et $u_3=(a_{31}, a_{32}, a_{33})$, en utilisant leur décomposition $u_1=a_{11}.i+a_{12}.j+a_{13}.k$ dans la base canonique $(i,j,k)$, et les valeurs induites précédemment. Par exemple, par linéarité (i) on doit avoir $[u_1,u_2,u_3]=[a_{11}i+a_{12}j+a_{13}k,u_2,u_3]=a_{11}[i,u_2,u_3]+a_{12}[j,u_2,u_3]+a_{13}[k,u_2,u_3]$. Par le même principe appliqué aux autres composantes, en écrivant $u_2=a_{21}i+a_{22}j+a_{23}k$ et $u_3=a_{31}i+a_{32}j+a_{33}k$ on extrait les coefficients $a_{ij}$ des produits mixtes de vecteurs de base. En supprimant tous ceux où deux d’entre eux apparaissent (condition (ii)), nous obtenons l’expression suivante : $[u_1,u_2,u_3]=a_{11}(a_{22}a_{33}[i,j,k]+a_{23}a_{32} [i,k,j])+a_{12}(a_{21}a_{33}[j,i,k]+a_{23}a_{31}[j,k,i])+a_{13}(a_{21}a_{32}[k,i,j]+a_{22}a_{31} [k,j,i]).$ Nous pouvons alors définir rigoureusement le produit mixte comme généralisation spatiale à trois vecteurs du déterminant à partir de l’expression obtenue :

Définition 1
Le produit mixte ou déterminant des vecteurs $u_1,u_2$ et $u_3$ est le nombre réel $det(u_1,u_2,u_3)=[u_1,u_2,u_3]=a_{11}(a_{22}a_{33}-a_{23}a_{32})-a_{12}(a_{21}a_{33}-a_{23}a_{31})+a_{13}(a_{21}a_{32}-a_{22}a_{31})$.

4.Produit mixte et orientation de l’espace

4.1.Orientation implicite d’une base de l’espace