La méthode analytique de Descartes, qui permet de représenter le plan euclidien comme le produit cartésien \(\mathbb R^2\) grâce à la théorie des nombres réels, permet également de représenter l’espace euclidien comme le produit cartésien \(\mathbb R^3=\mathbb R^2\times \mathbb R\). On y retrouve le point de vue alternatif des points ou des vecteurs, et le produit scalaire naturel, qui permet, grâce à la représentation des éléments de l’espace par coordonnées, de calculer la distance entre deux points comme la norme d’un vecteur.

1.L’ensemble \(\mathbb R^3\) comme représentation de l’espace euclidien

1.1.La représentation analytique \(\mathbb R^2\) du plan euclidien

L’approche analytique de Descartes permet de représenter le plan euclidien comme le produit cartésien \(\mathbb R^2\). Les éléments du plan sont donc les couples \((x,y)\) de nombres réels, considérés soit comme points, soit comme vecteurs. Quand on les considère comme vecteurs, ils se représentent de manière unique sous la forme \((x,y)=x.(1,0) +y.(0,1)\) : on dit que les vecteurs \(\vec i=(1,0)\) et \(\vec j=(0,1)\) forment une base (dite canonique) du plan vectoriel \(\mathbb R^2\). L’ordre dans lequel on considère ces deux vecteurs a son importance : la base \((\vec i,\vec j)\) détermine une orientation (directe) du plan euclidien, la base \((\vec j,\vec i)\) détermine l’autre orientation (indirecte) du plan. L’orientation directe est celle selon laquelle on considère que les angles orientés ont une mesure positive dans le sens trigonométrique.

1.2.L’approche analytique de représentation de l’espace

En utilisant la même approche, on peut représenter l’espace euclidien à trois dimensions à partir d’un produit cartésien, à savoir \(\mathbb R^3=\mathbb R^2\times \mathbb R\). Les éléments de \(\mathbb R^3\) sont les triplets \(((x,y),z)\) de nombres réels, c’est-à-dire les couples formés d’un couple \((x,y)\in\mathbb R^2\) et d’un élément \(z\in\mathbb R\). Pour simplifier cette description, on écrit \((x,y,z)\) un tel triplet, et on considère à nouveau les éléments de \(\mathbb R^3\) soit comme des points, soit comme des vecteurs. Il est important de comprendre que points et vecteurs ne sont ici que deux manières différentes de considérer les mêmes objets (géométrique pour les points, algébrique pour les vecteurs). Comme dans le plan euclidien, un vecteur \((x,y,z)\in\mathbb R^3\) se représente de manière unique sous la forme \((x,y,z)=x.(1,0,0)+y.(0,1,0)+z.(0,0,1)\), et les vecteurs \(\vec i=(1,0,0)\), \(\vec j=(0,1,0)\) et \(\vec k=(0,0,1)\) forment la base canonique de l’espace vectoriel \(\mathbb R^3\). Ici aussi, l’ordre \((\vec i,\vec j,\vec k)\) dans lequel on considère ces vecteurs détermine une orientation de l’espace.

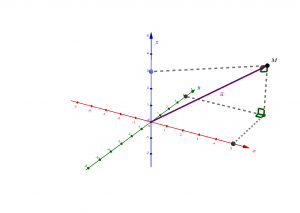
Le point \(M\) et le vecteur \(\vec u\) sont deux manières alternatives de considérer le même élément \(((5,4),3)\) de l’espace euclidien représenté comme l’ensemble \(\mathbb R^3=\mathbb R^3\times \mathbb R\). Les deux premières coordonnées \((5,4)\) sont celles de la projection de \(M\) dans le plan \(xOy\), la troisième coordonnée \(3\) correspond à la projection de \(M\) sur l’axe \(Oz\).

2.Le produit scalaire naturel dans \(\mathbb R^3\)