Le produit vectoriel représente une opération antilinéaire essentielle dans l’espace euclidien, transformant deux vecteurs en un troisième. Lorsque les deux vecteurs initiaux sont linéairement indépendants, ils forment, avec leur produit vectoriel — dont la norme est équivalente à l’aire du parallélogramme qu’ils engendrent —, une base directe. En partant du produit mixte pour définir théoriquement le produit vectoriel, on obtient une expression analytique précise de celui-ci. Cette expression analytique peut être induite en examinant les résultats des produits vectoriels calculés avec les vecteurs de la base canonique.

1.Le produit vectoriel : un produit de vecteurs

1.1.Problème : trouver l’équation d’un plan

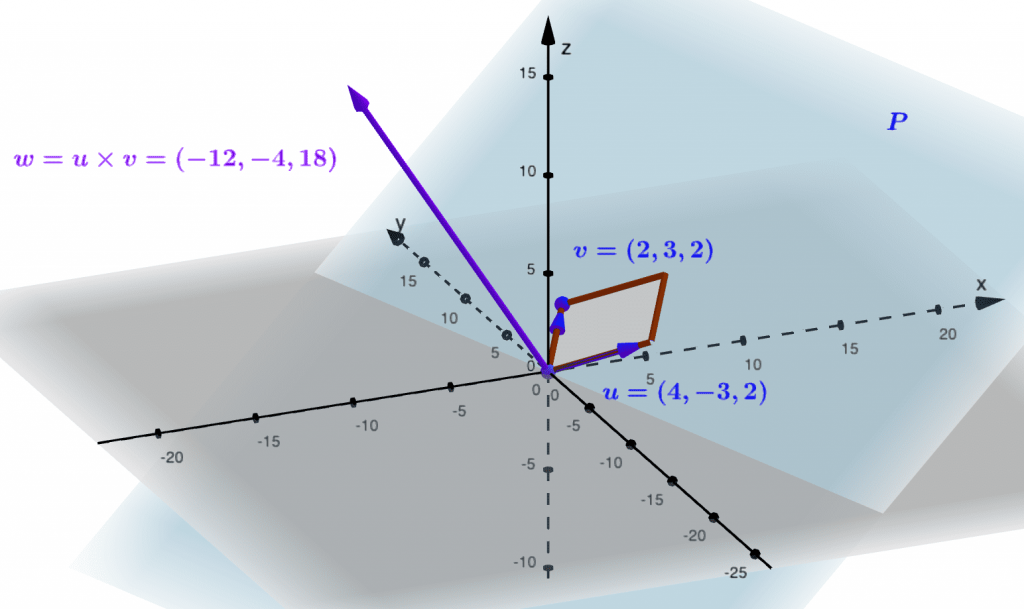
Dans l’espace euclidien $\mathbb R^3$, un plan (affine) $P$ est l’ensemble des points $(x,y,z)$ solutions d’une équation cartésienne du type $ax+by+cz=d$, avec $a,b$ ou $c$ non nul. Lorsqu’on dispose d’une telle équation, il est simple de trouver une base de la direction de $P$ – c’est-à-dire du plan vectoriel $P_0$ d’équation $ax+by+cz=0$ – et donc de décrire entièrement $P$, pour peu qu’on en connaisse un point. Mais le problème inverse est plus délicat : étant donnés deux vecteurs $u,v$ de l’espace, linéairement indépendants et donc formant une base $(u,v)$ d’un plan (vectoriel) $P_0$, comment trouver une équation d’un plan affine $P$ de direction $P_0$ ?

Connaissant un point de $P$, le problème se ramène à trouver une équation de $P_0$, et on peut le résoudre grâce à l’opération appelée produit vectoriel, qui transforme deux vecteurs de l’espace $u,v$ en un autre vecteur $w$, et de sorte que si $u$ et $v$ sont linéairement indépendants, alors le triplet de vecteurs $(u,v,w)$ forme une base directe de l’espace.

1.2.Solution : le produit vectoriel et l’orthogonalité

En effet, il existe de multiples manières de « compléter » $(u,v)$ en une base de l’espace, mais le produit vectoriel fournit une solution « canonique » (ou « standard ») en termes de direction, d’orientation et d’amplitude, dans le sens où :

1. Le vecteur $w$ est orthogonal à $u$ et $v$, et donc au plan $P_0$
2. La base $(u,v,w)$ est orientée dans le sens direct
3. La norme de $w$ est l’aire du parallélogramme déterminé par $u$ et $v$.

Or, ces propriétés entraînent que $P_0$ ne peut être que le plan vectoriel orthogonal à $w$, de sorte qu’en disposant d’une expression analytique de $w$ en fonction de $u$ et $v$, nous pouvons résoudre le problème du passage d’une base à l’équation d’un plan, même si le produit vectoriel a une signification plus profonde.

2.Définition du produit vectoriel

2.1.La forme linéaire associée au produit mixte

Les contraintes précédentes sont autant d’indications qui permettraient de donner une définition « heuristique » du produit vectoriel, comme nous l’avons fait pour le produit mixte. Nous allons plutôt nous appuyer sur cette dernière notion, afin d’en tirer une définition du produit vectoriel. Rappelons qu’une fonction $f:\mathbb R^3\to\mathbb R$ est dite linéaire (on parle alors de forme linéaire), si pour tous vecteurs $u,v\in\mathbb R^3$ et tout nombre réel $\lambda\in\mathbb R$, on a $f(u+\lambda v)=f(u)+\lambda.f(v)$. On démontre alors simplement la proposition suivante, qui permet de « représenter » les formes linéaires par produit scalaire avec un vecteur de l’espace :

Proposition 1
Si $f:\mathbb R^3\to \mathbb R$ est une forme linéaire, alors il existe un unique vecteur $u_f\in\mathbb R^3$ tel que pour tout $v\in\mathbb R^3$, on a $f(v)=u_f\cdot v$ ($u\cdot v$ dénote le produit scalaire de deux vecteurs $u$ et $v$).

En fait, le vecteur $u_f$ s’obtient de manière très simple : ses coordonnées sont les valeurs de la forme $f$ sur les trois vecteurs de la base canonique, c’est-à-dire $u_f=(f(i),f(j),f(k))$, avec $i=(1,0,0)$, $j=(0,1,0)$ et $k=(0,0,1)$.

Soient alors $u,v\in\mathbb R^3$ deux vecteurs de l’espace : si $w\in\mathbb R^3$ est un vecteur quelconque, le produit mixte $[u,v,w]=det(u,v,w)$ est un nombre réel, et par linéarité en la troisième composante, on définit une fonction linéaire $f:w\in\mathbb R^3\mapsto [u,v,w]\in\mathbb R$. Puisque $f$ est une forme linéaire, nous pouvons alors lui appliquer la proposition 1, pour définir le produit vectoriel :

Définition 1
Le produit vectoriel de $u$ et $v$ est l’unique vecteur de l’espace, noté $u\times v$, tel que pour tout vecteur $w\in\mathbb R^3$ on a $[u,v,w]=(u\times v)\cdot w$.

2.2.Expression analytique du produit vectoriel

Or, nous possédons une expression du produit mixte (produit mixte et orientation de l’espace, Définition 1) de trois vecteurs $u_1=(x_1,y_1,z_1)$, $u_2=(x_2,y_2,z_2)$ et $u_3=(x_3,y_3,z_3)$, sous la forme $$[u_1,u_2,u_3]=x_1(y_2z_3-z_2y_3)-y_1(x_2z_3-z_2x_3)+z_1(x_2y_3-y_2x_3).$$ A partir de celle-ci, on obtient alors une expression analytique du produit vectoriel $u\times v$ de deux vecteurs $u=(x_1,y_1,z_1)$ et $v=(x_2,y_2,z_2)$ à partir des valeurs de la forme linéaire $f:w\mapsto [u,v,w]$ sur les vecteurs de la base canonique. On trouve $f(i)=[u,v,i]=y_1z_2-y_2z_1$, $f(j)=z_1x_2-z_2x_1$ et $f(k)=x_1y_2-x_2y_1$, d’où l’expression suivante :

Proposition 2
Le produit vectoriel des vecteurs $u=(x_1,y_1,z_1)$ et $v=(x_2,y_2,z_2)$ est le vecteur $$u\times v=(y_1z_2-y_2z_1,z_1x_2-z_2x_1,x_1y_2-x_2y_1).$$

Dans la pratique, lorsqu’on calcule un produit vectoriel on peut écrire les deux vecteurs $u$ et $v$ sous forme de colonnes, et recopier les deux premières lignes en-dessous : $$\begin{array}{cc} x_1 & x_2\\y_1 & y_2\\z_1&z_2\\x_1 & x_2\\y_1 & y_2\end{array}$$ On effectue alors les trois calculs comme ceux de trois déterminants 2×2 à partir de la deuxième ligne : $y_1z_2-y_2z_1$, $z_1x_2-z_2x_1$ et $x_1y_2-x_2y_1$.

3.Propriétés du produit vectoriel

3.1.Propriétés algébriques

Le produit vectoriel étant défini à partir du produit mixte, il hérite de certaines propriétés essentielles associées au déterminant de trois vecteurs, qui sont résumées dans la proposition suivante :

Proposition 3
Si $u,v,w$ sont trois vecteurs de l’espace et $\lambda$ est un nombre réel, alors on a :
o) $u\cdot(u\times v)=0$
i) $v\times u=-u\times v$
ii) $0\times u=0$ ($0$ est le vecteur nul)
iii) $(\lambda u+v)\times w=\lambda.(u\times w)+v\times w$.

Ces propriétés se démontrent de manière élémentaire à partir de celles du produit mixte. Par antilinéarité (propriété (i)), les propriétés (o), (ii) et (iii) sont évidemment valables sur l’autre coordonnée. Considérons la première propriété : elle traduit le fait que par définition, on a $u\cdot (u\times v)=det(u,u,v)=0$, le déterminant étant nul si deux vecteurs sont identiques. C’est aussi vrai pour $v$, si bien que $u\times v$ est toujours orthogonal à $u$ et $v$, et donc au plan $P$ engendré par $u$ et $v$ si ceux-ci sont linéairement indépendants. Dans ce cas, cela signifie que $P$ est l’ensemble des vecteurs orthogonaux à $u\times v$, et nous pouvons alors résoudre le problème posé au début de l’article :

Corollaire 1
Si $u=(x_1,y_1,z_1)$ et $v=(x_2,y_2,z_2)$ forment une base du plan vectoriel $P$, alors une équation de $P$ est $a x+by+cz=0$, avec $a=y_1z_2-y_2z_1$, $b=z_1x_2-z_2x_1$ et $c=x_1y_2-x_2y_1.$

3.2.Interprétation géométrique

Supposons que $u$ et $v$ sont linéairement indépendants : par définition, leur produit vectoriel est l’unique vecteur $u\times v$ tel que pour tout vecteur $w$, on a $(u\times v)\cdot w=[u,v,w]$, c’est-à-dire le volume algébrique du parallélépipède orienté construit sur $u,v,w$. En appliquant cette égalité à $w=u\times v$ lui-même, on obtient $[u,v,u\times v]=(u\times v)\cdot (u\times v)=||u\times v||^2$. Comme $u\times v$ est orthogonal à $u$ et $v$ le triplet $(u,v,u\times v)$ est une base de l’espace euclidien. Par ce qui précède, son déterminant est positif, et on a donc :

Corollaire 2
Pour tous vecteurs linéairement indépendants $u,v$ de l’espace, le triplet $(u,v,u\times v)$ est une base directe de l’espace.

De plus, puisque $u\times v$ est orthogonal au plan $P$ engendré par $u$ et $v$, cela signifie que l’aire du parallélogramme construit sur $u$ et $v$ est obtenue en divisant le volume (algébrique) $||u\times v||^2$ du parallélépipède formé par $u,v,u\times v$ par sa hauteur, soit $||u\times v||$. Par conséquent, la norme de $||u\times v||$ est l’aire du parallélogramme construit sur $u$ et $v$. Le produit vectoriel $u\times v$, dans ce cas, est donc l’unique vecteur ayant les propriétés énoncées à la section 1.2 :

• $u\times v$ est orthogonal à $u$ et $v$
• $(u,v,u\times v)$ est une base directe de l’espace
• $||u\times v||$ est l’aire du parallélogramme construit sur $u$ et $v$.

Ainsi, le produit vectoriel permet de compléter de manière « canonique » (c’est-à-dire standard) un couple de vecteurs linéairement indépendants en une base de l’espace.

3.3.Expression de la norme du produit vectoriel

Nous savons que la norme du produit vectoriel $u\times v$ est l’aire du parallélogramme construit sur $u$ et $v$. Une expression très commode de cette norme, et donc un calcul analytique de cette aire, est possible à partir du produit scalaire de $u$ et $v$ et de leur normes :

Proposition 4
Si $u,v$ sont deux vecteurs de l’espace, alors on a $||u\times v||^2+(u\cdot v)^2=||u||^2.||v||^2.$

Il existe plusieurs démonstrations de cette égalité. Sans disposer du double produit vectoriel et de l’interprétation trigonométrique du produit vectoriel, on peut procéder de manière analytique, c’est-à-dire par le calcul, en écrivant à nouveau $u=(x_1,y_1,z_1)$ et $v=(x_2,y_2,z_2)$. On a : $\begin{eqnarray} ||u\times v||^2+(u\cdot v)^2 &=&(y_1z_2-y_2z_1)^2+(z_1x_2-z_2x_1)^2+(x_1y_2-x_2y_1)^2+(x_1x_2+y_1y_2+z_1z_2)^2\\&=&y_1z_2^2+y_2z_1^2+z_1^2x_2^2+z_2^2x_1^2+x_1^2y_2^2+x_2^2y_1^2+x_1^2x_2^2+y_1^2y_2^2+z_1^2z_2^2\\&=&(x_1^2+y_1^2+z_1^2).(x_2^2+y_2^2+z_2^2)=||u||.||v||^2,\end{eqnarray}$
les double-produits s’annulant deux-à-deux après la première égalité.

4.Bases orthonormées et quaternions

4.1.Produit vectoriel des vecteurs de la base canonique