A partir de l’approche analytique de Descartes, qui consiste à introduire des coordonnées pour représenter les points du plan, et de la construction de Cauchy des nombres réels, on peut donner une représentation moderne du plan à partir de laquelle on retrouve les axiomes géométriques d’Euclide.

1. L’approche synthétique d’Euclide (et de Hilbert)

1.1. La géométrie plane d’Euclide

Le mathématicien grec Euclide est fameux pour ses postulats et axiomes de la géométrie plane, concernant les droites, les segments, les cercles, les angles, le parallélisme, la perpendicularité… et jusqu’à aujourd’hui, on les utilise pour la géométrie du plan, concernant ces objets, et appelée précisément la géométrie euclidienne (plane). Cette approche est ce qu’on appelle en mathématique une approche synthétique : à partir d’axiomes, qui relèvent d’une formulation de l’intuition de propriétés élémentaires d’objets mathématiques, on établit des propriétés grâce à des déductions (démonstrations), ne faisant pas intervenir de calcul.

1.2. La complétion de Hilbert et la question du calcul

L’approche euclidienne, valable depuis l’Antiquité, présente toutefois certaines limites. D’une part, il manque » des axiomes pour démontrer tous les théorèmes d’Euclide (certaines démonstrations faisaient implicitement référence à des propriétés non établies), ce à quoi le mathématicien allemand David Hilbert, notamment, a remédié en 1899 en proposant une liste d’axiomes plus complète. D’autre part, dans la mathématique grecque ancienne les calculs « d’aires », comme dans le théorème de Pythagore, sont en fait des énoncés sur des recompositions de figures géométriques : l’approche synthétique n’est pas articulée au calcul, ce qui fait défaut à son interprétation dans la mathématique moderne.

D. Hilbert

2. L’approche analytique de Descartes : les coordonnées et le calcul

2.1. La méthode analytique de Descartes : les coordonnées

A l’époque moderne, le mathématicien et philosophe français René Descartes invente les « coordonnées » d’un point du plan : on peut représenter un tel point M par un couple (x,y) de nombres, x étant l’abscisse et y étant l’ordonnée du point M. Ces coordonnées correspondent aux projections du point M, perpendiculairement, sur deux « axes ».

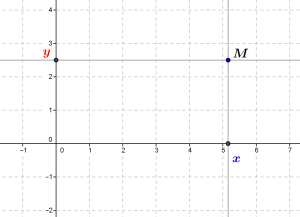
Ceci permet d’introduire le calcul dans la géométrie plane, puisqu’on peut alors par exemple représenter les droites par des équations; l’intersection de deux droites non parallèles est un point, dont on peut déterminer les coordonnées par des procédés « analytiques », c’est-à-dire ici calculatoires, à partir d’équations des deux droites ou de paramètres numériques qui les décrivent.

2.2. Les grandeurs géométriques incommensurables : utiliser les nombres réels

Cependant, si cette méthode est bien adaptée à ce qu’on appelle la « géométrie affine » (la partie de la géométrie qui a trait aux droites et au parallélisme dans ce contexte), à l’époque les nombres rationnels ne suffisent pas pour traiter de certaines grandeurs liées notamment aux triangles et aux cercles. En effet, d’après le théorème de Pythagore si nous voulons assigner une mesure de longueur à la diagonale d’un triangle rectangle, celle-ci doit être une racine carrée de la somme des carrés des longueurs des deux autres côtés.

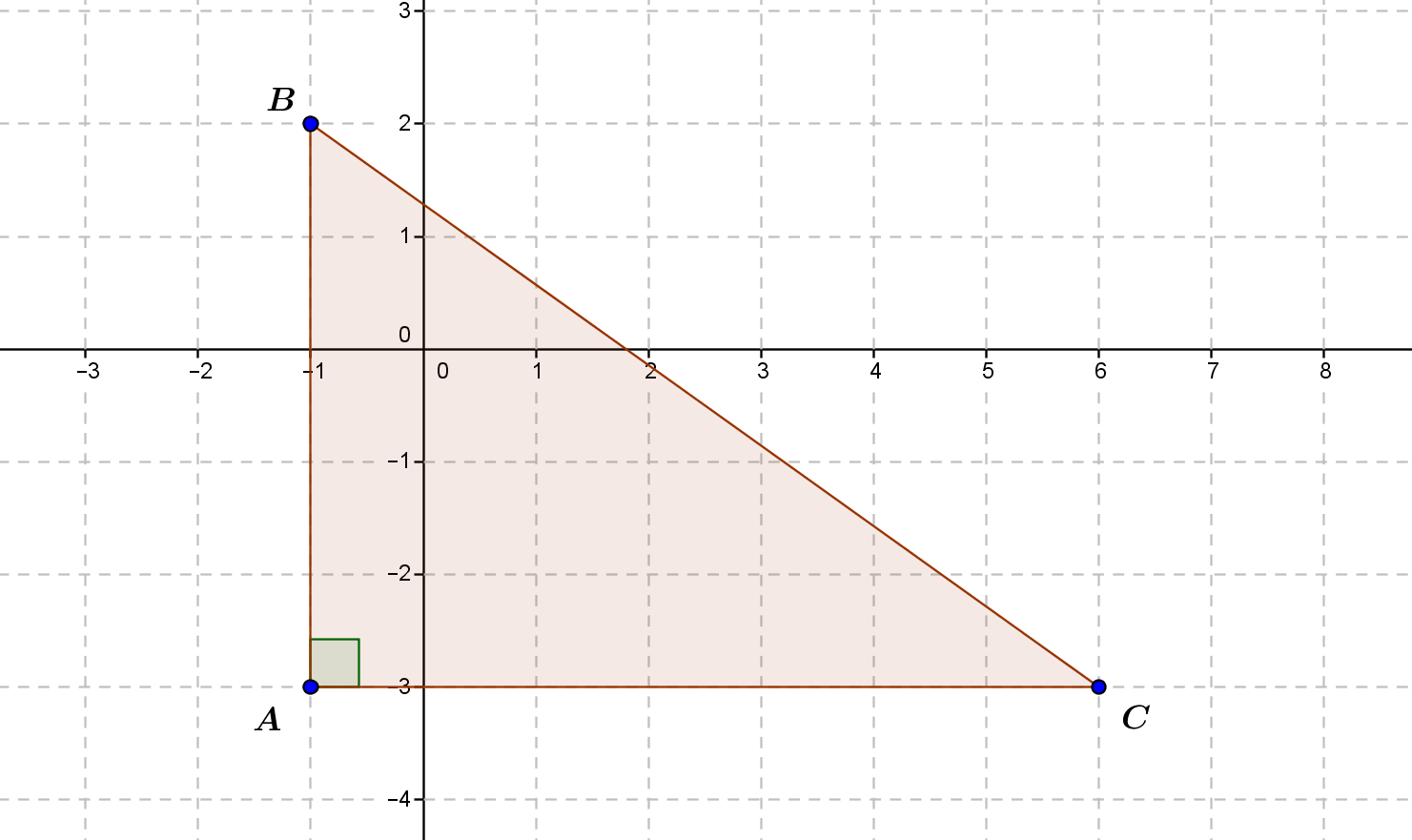
Dans le triangle \(ABC\) rectangle en \(A\), par le théorème de Pythagore l’aire du carré construit sur l’hypoténuse (soit le segment \([BC]\)) est la somme des aires des carrés construits sur les côtés \([AB]\) et \([BC]\). Ainsi, le carré \(BC^2\) de la longueur \(BC\) du côté \([BC]\) devrait être égale à la somme \(AB^2+AC^2\), soit ici \(5^2+7^2=25+49=74\), ou encore \(BC=\sqrt{74}\).

Or, lorsqu’on mesure, dans la tradition antique, des longueurs par des nombres rationnels, une telle racine carrée n’existe pas toujours. Par exemple, la diagonale d’un carré de longueur \(1\) doit être un nombre dont le carré vaut \(2\), et on peut démontrer que ce nombre n’existe pas, ce qui était connu dès l’Antiquité et constituait une véritable tragédie… grecque. On dit que « la diagonale du carré unité est incommensurable ».

Pour que l’approche analytique soit utile pour toute la géométrie euclidienne, il faut donc qu’elle puisse s’appliquer à tous ses objets, et notamment les angles et les cercles. C’est grâce à la construction des nombres réels que la possibilité de le faire a été fondée sur des bases solides.

R. Descartes

3. Représenter le plan euclidien grâce à l’ensemble des nombres réels

3.1. Les nombres réels au-delà des limitations traditionnelles

La construction des nombres réels (voir l’article Qu’est-ce qu’un nombre réel ?) a permis de résoudre le problème de « l’existence » de certaines grandeurs qu’il n’était pas possible de trouver dans l’ensemble des nombres rationnels, comme certaines solutions d’équations numériques (dites diophantiennes), et en particulier l’existence de racines carrées pour tous les nombres positifs.

En particulier, en ce qui concerne la traduction dans ou par le calcul des propriétés de la géométrie euclidienne, les limites de l’approche cartésienne par coordonnées associées au calcul des longueurs, sont levées si l’on veut bien concevoir que les coordonnées d’un point du plan sont des nombres réels et pas des nombres rationnels. Autrement dit, la tragédie « pythagoricienne » de l’incommensurabilité de la diagonale du carré unité a trouvé une fin heureuse à l’époque moderne, mais la civilisation grecque n’en a pas profité (pour ce que nous en savons).

3.2. \(\mathbb R^2\) comme représentation ensembliste du plan euclidien

Mais on peut interpréter aujourd’hui cette application de la théorie des nombres réels à la géométrie euclidienne comme la refondation possible de cette géométrie antique sur des bases modernes, « analytiques ». En effet, à partir de l’idée cartésienne qu’on peut représenter un point du plan à partir de ses coordonnées, qui sont désormais un couple \((x,y)\) de nombres réels, on peut en fait définir un point du plan comme un tel couple \((x,y)\) de nombres réels !

Ainsi, on peut décréter que le « plan euclidien », c’est l’ensemble des couples \((x,y)\) de nombres réels, et les ressources de la théorie naïve des ensembles (voir l’article Qu’est-ce qu’un ensemble ?) nous permettent d’en donner une description parfaitement claire comme ce qu’on appelle le produit cartésien (adjectif tiré de « Descartes ») de l’ensemble \(\mathbb R\) des nombres réels par lui-même, soit l’ensemble noté \(\mathbb R\times\mathbb R\) ou encore \(\mathbb R^2\). Cette façon de faire est bien adaptée à la rigueur mathématique moderne, qui repose sur la théorie des ensembles, et intègre à la fois l’approche calculatoire par coordonnées, et l’approche synthétique par axiomes. En effet, on peut démontrer que tous les axiomes de Euclide (et de Hilbert) sont « vrais » dans le plan \(\mathbb R^2\), si du moins on « interprète » les droites, les points, les segments, les cercles, les angles, le parallélisme, la perpendicularité… dans ce nouveau langage, ce qui est l’objet de l’algèbre linéaire et de la géométrie affine euclidienne. On a trouvé ce qu’on appelle un modèle de la géométrie euclidienne.

3.3. La distance euclidienne dans la géométrie moderne du plan

Un des éléments-clefs de cette interprétation est la notion de distance euclidienne : en s’inspirant du théorème de Pythagore, on peut considérer que la distance entre deux points \(A=(a_1,a_2)\) et \(B=(b_1,b_2)\) est la longueur de l’hypoténuse du triangle rectangle « défini » par ces deux points, et on la définit ainsi comme le nombre réel dont le carré vaut \((b_1-a_1)^2+(b_2-a_2)^2\), soit \[\sqrt{(b_1-a_1)^2+(b_2-a_2)^2},\] puisque \(|b_1-a_1|\) et \(|b_2-a_2|\) sont les longueurs des côtés du triangle, comme sur la figure suivante (le signe |.| est la valeur absolue : la valeur absolue \(|x|\) d’un nombre \(x\) est celui des nombres \(x\) ou \(-x\) qui est positif, et \(x^2=|x|^2\) pour tout réel \(x\)).

Il faut noter que le plan euclidien \(\mathbb R^2\) est la « structure de base » pour la définition de l’ensemble \(\mathbb C\) des nombres complexes : un nombre complexe, ce n’est rien d’autre, de ce point de vue, qu’un point du plan euclidien, considéré « muni » d’une structure algébrique et géométrique particulière. Mais ceci est une autre histoire.

4. Au-delà d’Euclide et Pythagore : la géométrie différentielle

4.1. Fécondité de la représentation analytique

Si la solution au problème de la description analytique de la géométrie euclidienne est apparue à l’époque moderne et a pu être formalisée grâce à la construction des nombres réels, ce n’est pas un hasard. Cette construction s’inscrit dans une période de développement scientifique et technique où l’on étudie les fonctions et où l’on s’intéresse désormais, avec la science moderne, aux procédés infinitésimaux (continuité, dérivation…).

Or, l’introduction de la description du plan euclidien comme \(\mathbb R^2\) présente des retombées bien plus avancées que la géométrie euclidienne. Alors que celle-ci ne s’occupe que de droites, de points, de cercles… ce qui correspondait aux préoccupations scientifiques et techniques de l’Antiquité, la méthode analytique permet de traiter désormais de la géométrie différentielle, c’est-à-dire de toutes les formes et mouvements, ayant une certaine régularité, dans le plan, l’espace et en dimensions supérieures.

4.2. Retour à la méthode synthétique dans la mathématique supérieure

Il est donc fort curieux à cet égard qu’une discipline mathématique récente, la géométrie différentielle synthétique, permette de reconstruire toute la géométrie différentielle – et potentiellement ses applications à la physique moderne – à partir d’une approche qui retourne « en arrière » à la démarche d’Euclide, soit à l’aide d’axiomes, en amont de toute forme de calcul. Il s’agit ici peut-être d’une expression du caractère intemporel unique de la science mathématique.

Euclide d’Alexandrie

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :

Pour aller plus loin

Commencer en mathématiques : Mathesis I.1 – Entrer dans l’Univers Mathématique