La division des entiers naturels ne donne pas toujours un résultat entier, et la division euclidienne donne une meilleure approximation de ce résultat, sous la forme d’un quotient et d’un reste. On peut définir une addition et une multiplication « modulaires » sur les restes, transformations de l’addition et la multiplication classiques. En étendant la division euclidienne aux entiers relatifs, on s’aperçoit que leur soustraction se transforme en une soustraction modulaire entre restes positifs.

1. La division euclidienne des entiers naturels

1.1. Division des entiers et partages des ensembles finis

Etant données deux quantités finies \(n\) et \(b\), autrement dit deux entiers naturels, avec \(b\) bon nul, la division de \(n\) par \(b\) ne donne pas toujours un résultat exact, ce qui signifie que \(n\) n’est pas toujours divisible par \(b\). Ceci traduit la situation suivante : étant donné un lot de \(n\) objets, il n’est pas toujours possible de le partager en lots de \(b\) objets sans reste. On la traduirait de manière combinatoire sous la forme suivante : étant donné un ensemble \(E\) de \(n\) objets, il n’est pas toujours possible de décomposer \(E\) en une réunion de sous-ensembles \(B_1,B_2,\ldots,\) de \(b\) objets deux-à-deux disjoints.

1.2. Principe de la division euclidienne

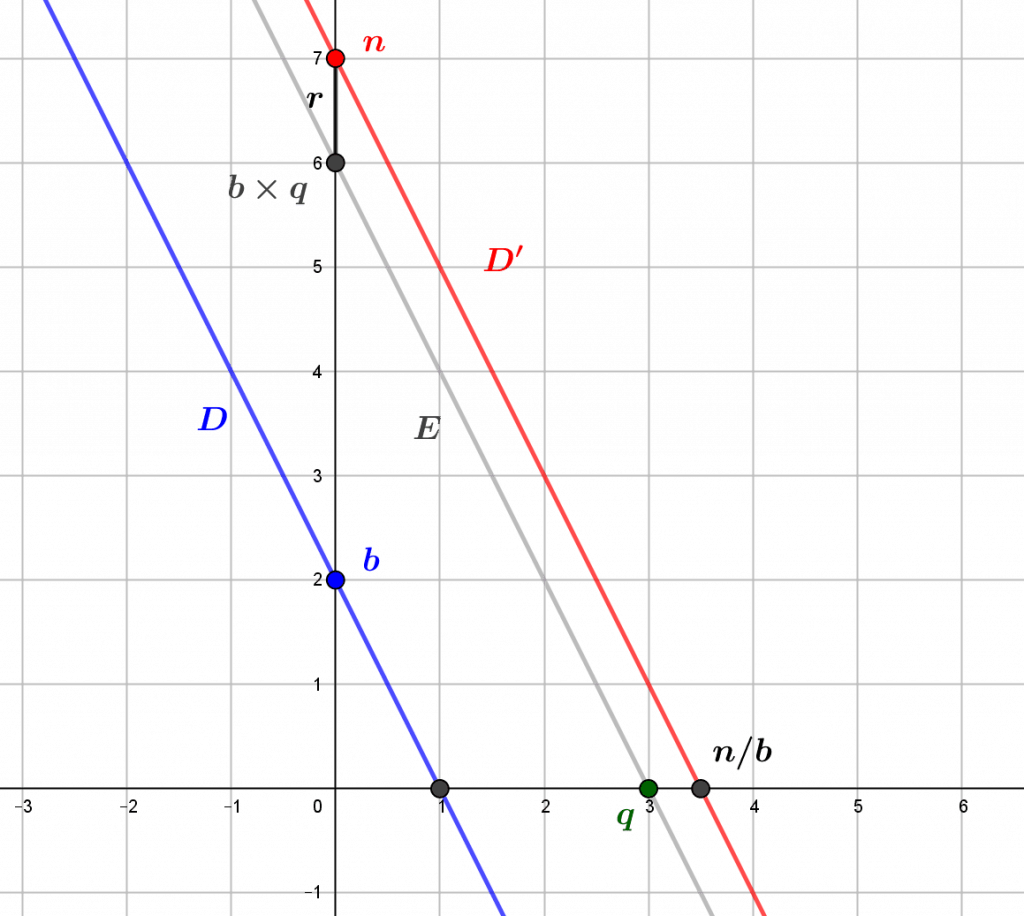
La division euclidienne des entiers naturels traduit cette situation arithmétique et combinatoire en fournissant une approximation entière de la division de \(n\) par \(b\), c’est-à-dire de \(n\) en \(b\) parties égales. Cette approximation se présente sous la forme d’une décomposition \(n=b\times q+r\), qu’on appelle division euclidienne de \(n\) par \(b\). L’entier naturel \(q\) est appelé quotient de cette division, c’est le nombre maximal de sous-ensembles à \(b\) éléments (deux-à-deux disjoints) qu’on peut former dans un ensemble à \(n\) éléments : c’est donc la meilleure approximation de la division de \(n\) par \(b\). L’entier naturel \(r\) est appelé reste de la division euclidienne de \(n\) par \(b\), c’est ce qui manque éventuellement à la division pour être exacte : on a donc \(r < b\), sinon \(q\) n’est pas la meilleure approximation.

1.3. Le théorème de la division euclidienne

L’intuition nous suggère que la division euclidienne de \(n\) par \(b\) ne peut nous donner qu’un seul résultat. Effectuer cette division, c’est donc trouver les seuls nombres entiers naturels \(q\) (le quotient) et \(r\) (le reste) tels qu’on peut écrire \(n=b\times q+r\), avec \(r< b\). Mais la division euclidienne est aussi un résultat théorique, qui s’énonce proprement sous la forme suivante :

Théorème 1
Etant donnés deux entiers naturels \(n\) et \(b\) quelconques avec \(b>0\), il existe deux entiers naturels uniques \(q\) et \(r\) tels que \(a=b\times q+r\) et \(r<b\).

Donnons une idée de la démonstration de ce théorème. Soit $D$ l’ensemble des entiers naturels $d$ tels que $d\times b\leq a$. L’ensemble $D$ n’est pas vide, puisqu’il contient $0$, et tout élément $d$ de $D$ est inférieur à $a$. C’est donc un ensemble fini, qui contient un plus grand élément, notons-le $q$. Par définition de $q$, on a $b.q\leq a$, et $q+1\notin D$, donc $a<b(q+1)$. Ecrivons $r=a-bq$ : en soustrayant $bq$ (dans $\mathbb Z$) de l’inégalité précédente, par les propriétés de $<$ on obtient $0=bq-bq\leq r=a-bq<b(q+1)-bq=b$, donc on peut écrire $a=b.q+r,$ avec $0\leq r<b$ : nous avons démontré l’existence de $q$ et de $r$. Supposons maintenant que $q’$ et $r’$ sont des entiers naturels avec la même propriété, c’est-à-dire que $a=b.q’+r’$, avec $r'<b$ : on a $b.q+r=b.q’+r’$, et en soustrayant $b.q’+r$ à chaque membre, on obtient $b.q-b.q’=r’-r$ $(*)$. Comme $r,r’\leq b-1$, on a $1-b\leq -r\leq 0$, d’où $-b+1\leq r’-r\leq b-1$ et $|r’-r|<b$ par définition de la valeur absolue. De l’égalité $(*)$, on en déduit que $b.|q-q’|<b$ et en divisant par $b>0$ on obtient $|q-q’|<1$, soit $q=q’$. Il s’ensuit alors que $0=a-a=(b.q+r’)-(b.q+r)=r’-r $, donc $r=r’$ et finalement, $q$ et $r$ sont uniques. On a démontré l’unicité de $q$ et $r$.

Exemple 1
Divisons $174$ par $23$ : on a $23\times 7=161$ et $23\times 8=184$, donc le quotient de la division euclidienne de $174$ par $23$ est $7$, et le reste est $174-23\times 7=13$.

2. L’addition modulaire

2.1. Le reste de la somme de deux entiers

Quel est le reste de la division euclidienne de $m+n$ par $b$ ? Si on additionne $m$ et $n$ à partir des expressions précédentes, on obtient $m+n=b.(q_1+q_2)+(r_1+r_2)$ : cette écriture se présente comme une division euclidienne, mais il est possible de $r_1+r_2\geq b$. Par exemple, divisons $m=17$ et $n=23$ par $4$ : on a $m=4.4+1$ et $n=5.4+3$, et la somme des deux restes est $4$. L’expression précédente n’est donc pas toujours celle de la division euclidienne de $m+n$ par $b$ : on peut obtenir n’importe quel nombre compris entre $0$ et $2b-2$. En revanche, si on fait une nouvelle division euclidienne de $r_1+r_2$ par $b$, dans tous les cas on obtient le reste de la division de $m+n$ par $b$ :

Proposition 1
Si $m$ et $n$ sont deux entiers naturels et $b$ est un entier naturel $>0$, soient $r_1$ et $r_2$ les restes de la division euclidienne de $m$ et $n$ par $b$. Le reste de la division euclidienne de $m+n$ par $b$ est le reste de la division euclidienne de $r_1+r_2$ par $b$.

Le reste de la division de $m+n$ par $b$ possède une interprétation combinatoire naturelle : si $E$ est un ensemble à $m$ éléments et $F$ un ensemble à $n$ éléments et si $E$ et $F$ sont disjoints, alors on peut trouver $q_1$ sous-ensembles de $E$, et $q_2$ sous-ensembles de $F$, à $b$ éléments. Mais les $r_1$ éléments restant dans $E$ et les $r_2$ éléments restant dans $F$ peuvent éventuellement former un ensemble supplémentaire à $b$ éléments.

2.2. L’addition modulo une base de division

Ainsi, pour trouver le reste de la division euclidienne de la somme de deux entiers naturels par un entier naturel $b>0$, il suffit de savoir le faire sur les restes possibles de cette division, qui sont les entiers naturels de $0$ à $b-1$, soit les nombres $0,1,\ldots,b-1$. Ceux-ci forment un ensemble qu’on note ici $[[0,b-1]]$ (segment de nombres entiers), et le calcul des restes de leurs somme est en quelque sorte une nouvelle addition « modulo $b$ » : si $x,y\in [[0,b-1]]$, on définit $x+y$ « modulo $b$ », comme le reste de la division euclidienne de $x+y$ par $b$. Pour ne pas confondre cette opération et son résultat avec la somme ordinaire, nous l’écrirons $x\oplus y$.

Exemple 2
Par exemple, soit $b=6$. On a $3\oplus 2=5$, puisque $3+2=5<6$ (donc $5$ est le reste de la division de $3+2$ par $6$). En revanche, on a $4\oplus 5=3$, puisque $4+5=6.1+3$ est la division euclidienne de $9=4+5$ par $6$.

Ainsi, alors que la somme $x+y$ de deux restes $x,y\in [[0,b-1]]$ est un entier naturel dans l’ensemble $\{0,\ldots,2b-2\}=[[0,b-2]]$, la somme modulaire $x\oplus y$ est un entier qui reste compris entre $0$ et $b-1$.

2.3. Propriétés de l’addition modulaire

Si nous avons appelé l’opération qui associe à deux restes $x$ et $y$ modulo $b>0$ une addition modulaire, c’est parce qu’elle possède toutes les propriétés élémentaires de l’addition des entiers naturels, résumées dans l’énoncé suivant :

Proposition 2
Si $x,y$ et $z$ sont trois entiers naturels de l’ensemble $[[0,b-1]]$, alors on a :
i) $x\oplus 0=x$
ii) $x\oplus y=y\oplus x$
iii) $x\oplus (y\oplus z)=(x\oplus y)\oplus z$.

Cette proposition se démontre en écrivant les divisions euclidiennes de $x+y$, de $x+(y\oplus z)$ et $(x\oplus y)+z$ et en utilisant l’unicité du quotient et du reste dans la division euclidienne.

3. La multiplication modulaire

3.1. Le reste du produit

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :