la Règle et le Compas
Explorez l’Infini
Une approche philosophique
de la science mathématique
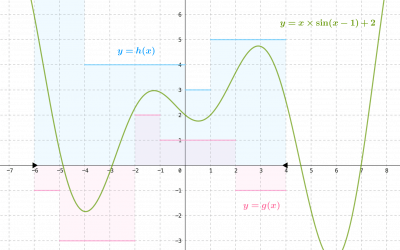
L’intégrale selon Riemann : fonctions continues sur un segment
Quelle est l'opération inverse de la dérivée d'une fonction ? Une première réponse à cette question consiste à intégrer une fonction qu'on veut pouvoir considérer comme dérivée, afin d'en construire une primitive. Cette problématique conduit naturellement à...
Polynômes irréductibles à coefficients réels et complexes
Les propriétés des polynômes à une indéterminée sur un corps sont analogues à celles des nombres entiers relatifs. En exploitant cette analogie à partir de la notion de polynôme irréductible, on en tirer des informations précieuses sur l'arithmétique des polynômes, et...
Fractions rationnelles : entre fonctions et arithmétique
Les fractions rationnelles à une indéterminée apparaissent à la convergence de la théorie des fonctions rationnelles et de la théorie des polynômes. En généralisant la construction des nombres rationnels à partir des nombres entiers relatifs, on les construit comme...
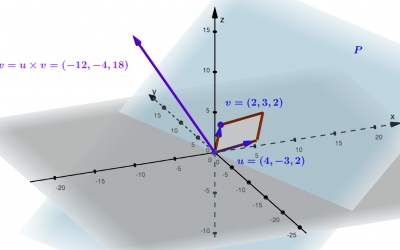
Produit vectoriel dans l’espace euclidien
Le produit vectoriel représente une opération antilinéaire essentielle dans l'espace euclidien, transformant deux vecteurs en un troisième. Lorsque les deux vecteurs initiaux sont linéairement indépendants, ils forment, avec leur produit vectoriel — dont la norme est...
Produit mixte et orientation dans l’espace euclidien
Le plan euclidien acquiert une orientation naturelle par le choix d'une base, que l'on peut qualifier de directe ou d'indirecte. Cette orientation se manifeste à travers le signe du déterminant de la base, correspondant à l'aire algébrique du parallélogramme orienté...
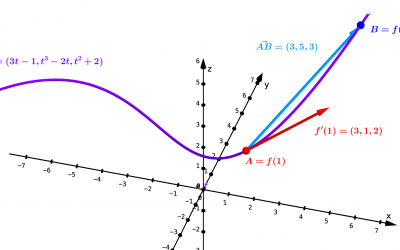
La représentation mathématique du mouvement
L'approche mathématique de la physique s'initie souvent par la description du mouvement. Cette démarche s'appuie sur la conceptualisation du mouvement en tant que variation de position en fonction du temps, ce qui conduit à sa modélisation comme une fonction...
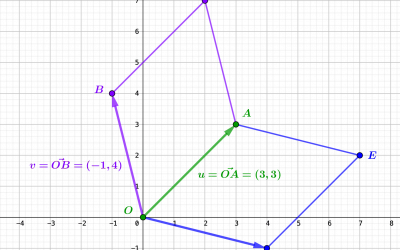
L’interprétation géométrique du déterminant dans le plan
Le produit scalaire et le déterminant sont des concepts clés de l'algèbre linéaire dans le plan euclidien, offrant une compréhension profonde des relations entre deux vecteurs $u$ et $v$. Lorsque ces vecteurs sont unitaires, leur produit scalaire et déterminant...
Les nombres cardinaux : quantifier l’infini
Quand il s'agit de compter ou de classer des ensembles, nous faisons appel à deux types de nombres : les ordinaux et les cardinaux. Alors que les nombres ordinaux nous aident à mettre en ordre une série d'éléments (premier, deuxième, troisième, etc.), les nombres...
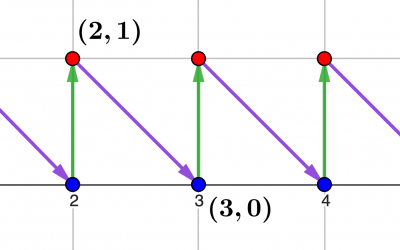
Les nombres ordinaux : compter dans l’infini
Les nombres entiers naturels ont deux visages : d'un côté, ils peuvent être vus comme des séquences ou des "énumérations" – ce qu'on appelle les nombres ordinaux. De l'autre, ils sont perçus comme des "quantités", ce qui nous mène aux nombres cardinaux. Bien que cette...
Implication matérielle et inférence logique : une confusion fréquente
Dans les discussions mathématiques, on entend parfois dire que "le faux implique n'importe quoi", et ce slogan est souvent déformé en : "à partir de quelque chose de faux, on peut démontrer que n'importe quoi est vrai", ce qui est parfaitement absurde. Ce malentendu...
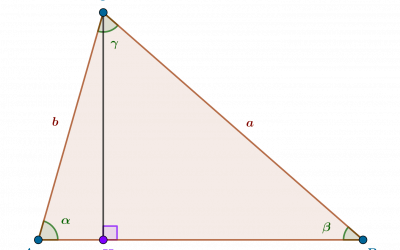
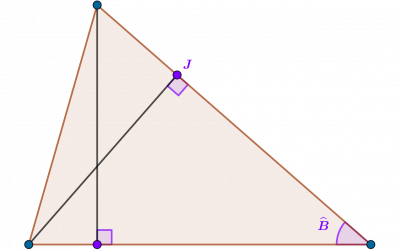
Loi des sinus, aire du triangle et formule de Héron
Introduction Dans Produit scalaire et loi des cosinus, nous avons montré à partir des angles orientés comment l'interprétation trigonométrique du produit scalaire de deux vecteurs conduisait à une généralisation du théorème de Pythagore, la "loi des cosinus" ou...
La construction axiomatique de l’arithmétique naturelle
L'arithmétique naturelle est la science des nombres entiers naturels : elle repose sur l'addition, la multiplication, l'ordre naturel et la divisibilité. Or, toutes ces opérations et relations se définissent à partir de la seule fonction successeur, dont les...
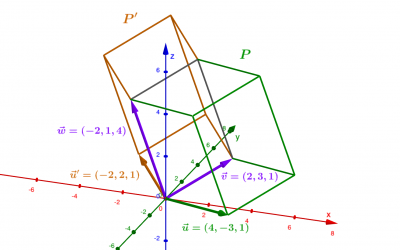
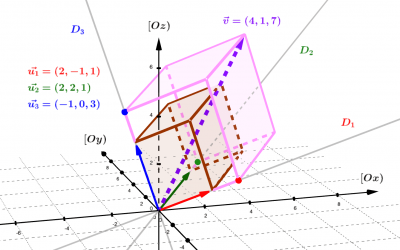
Les bases de l’espace euclidien
Comme dans le plan euclidien $\mathbb R^2$ , il existe dans l'espace euclidien $\mathbb R^3$ une infinité de bases ou "systèmes de représentation" des vecteurs : l'espace étant intuitivement de dimension 3, ces bases sont toujours formées de 3 vecteurs non nuls. La...
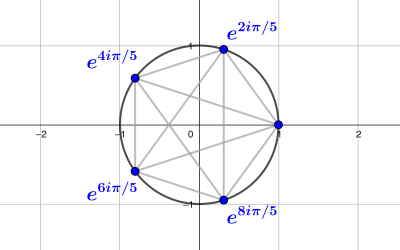
Racines carrées dans les corps finis : le cas de -1 et le critère d’Euler
Les corps finis traduisent sur le plan structurel certaines propriétés arithmétiques et servent de "corps de restes" en théorie des nombres. Par analogie avec les corps $\mathbb R$ des nombres réels et $\mathbb C$ des nombres complexes, le nombre $-1$ peut y posséder...
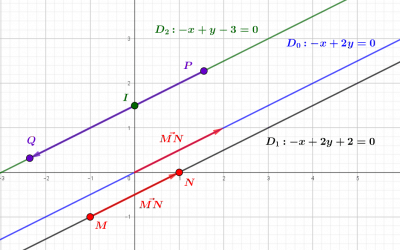
Equations cartésiennes : la description analytique des droites du plan
L'approche analytique de la géométrie plane, que nous devons à Descartes, permet de donner une description purement algébrique des droites du plan comme ensembles de solutions d'équations d'un seul type. Ces équations dites cartésiennes contiennent toute l'information...
Définir l’aire du triangle et du parallélogramme
Dans la géométrie intuitive on définit les aires des figures sans justification ou sans démonstration. Dans la géométrie euclidienne moderne, c'est-à-dire analytique, la définition de l'aire du triangle et du parallélogramme se fondent sur des définitions univoques de...
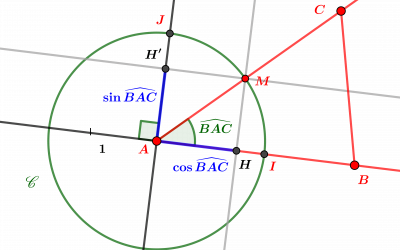
Loi des cosinus et produit scalaire de deux vecteurs
On rencontre souvent en géométrie et en physique une expression trigonométrique du produit scalaire. A partir d'une définition du cosinus et du sinus d'un angle affine, on peut la démontrer directement grâce aux propriétés élémentaires du produit scalaire. On tire de...
Anneaux d’entiers quadratiques et ramification des nombres premiers
L'anneau des entiers de Gauss \(\mathbb Z[i]\) possède des propriétés remarquables, analogues à celles de l'ensemble \(\mathbb Z\) des nombres entiers relatifs. Il existe toute une famille de tels anneaux, possédant des propriétés similaires, et définis aussi à partir...
Les corps finis : une approche structurelle de l’arithmétique
Les corps sont les anneaux dont tout élément non nul est inversible. Tous les anneaux intègres finis sont des corps, et tous ces corps finis sont commutatifs. Avec un peu d'algèbre commutative, on peut même décrire entièrement tous les corps finis, qui correspondent...
Nombres premiers entre eux et inversion modulaire
Deux nombres entiers sont dits premiers entre eux si ils n'ont pas de facteur premier en commun : il sont donc premiers "l'un par rapport à l'autre". Le nombre des restes modulo un entier naturel non nul $n$ qui sont premiers avec $n$ est ce qu'on appelle l'indicateur...