Les nombres réels sont toutes les « grandeurs » qu’on peut ordonner, et on peut les « construire » de diverses manières grâce à la théorie des ensembles

« Les nombres gouvernent le monde. » Pythagore

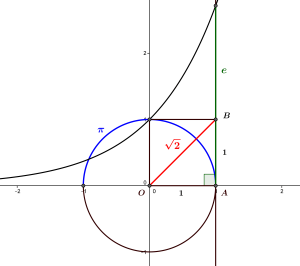
Introduction : les grandeurs irrationnelles

Les nombres réels idéalisent tous les « points » de la droite géométrique, ou du point de vue arithmétique toutes les « mesures » de grandeur possibles. Les Anciens savaient grâce au théorème de Pythagore que l’on ne pouvait mesurer la diagonale du carré de côté 1 par un nombre rationnel, c’est-à-dire fractionnaire, de la forme \(\dfrac a b\) pour \(a\) et \(b\) des nombres entiers (on dit que cette diagonale est incommensurable). Aujourd’hui, on dirait que la longueur de cette diagonale est \(\sqrt 2\) (voir l’article L’irrationalité de \(\sqrt 2\) : une tragédie pythagoricienne). On a depuis découvert une foultitude de « grandeurs » qui ne sont pas des nombres rationnels, comme \(\pi\), le rapport de la circonférence d’une cercle à son diamètre, ou \(e\), la base de l’exponentielle. Les nombres réels théorisent toutes ces grandeurs qui peuvent être « ordonnées », comme les nombres rationnels, mais qui excèdent ceux-ci, en quelque sorte. Ils peuvent être construits dans un sens mathématique précis, à partir des nombres rationnels, de plusieurs manières : les plus fameuses sont sans doute la méthode des suites de Cauchy, et celle des coupures de Dedekind.

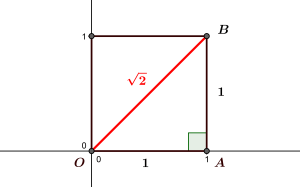
La diagonale du carré de côté \(1\) est « incommensurable » : par le théorème de Pythagore, on a \(OA^2+AB^2=OB^2\), si bien que \(OB^2=2\); or, on peut démontrer qu’il n’existe pas de nombre rationnel \(r\) dont le carré vaut \(2\), si bien que la longueur \(OB\) ne peut pas être un nombre rationnel.

1. Il y a des « trous » dans l’ensemble des nombres rationnels

1.1. Le problème avec l’axiomatisation du continu

Comme nous l’avons vu avec les entiers naturels (voir l’article Qu’est-ce qu’un entier naturel ?), pour théoriser un type d’objet mathématique on s’intéresse à l’ensemble des objets de ce type, dont on essaie d’identifier des propriétés fondamentales (« postulats » ou « axiomes »). Il en va de même pour les nombres réels : même si l’intuition de ce qu’ils sont nous est plus ou moins accessible, la théorie mathématique à leur propos va consister à décrire un ensemble, noté \(\mathbb R\), des nombres réels.

Contrairement toutefois au cas des entiers naturels, il n’est pas évident de donner des propriétés intuitives élémentaires qui décriraient cet ensemble en le différenciant nettement de l’ensemble \(\mathbb Q\) des nombres rationnels. Par exemple, l’idée de « continuité » d’une droite géométrique peut s’exprimer en disant que pour deux points A et B de cette droite, il existe toujours un point C strictement compris entre A et B : on peut « remplir » indéfiniment les espaces déterminés par deux points. Or, cette propriété est déjà vérifiée pour les nombres rationnels : si \(x,y\) sont de tels nombres, tels que \(x<y\), on peut montrer facilement qu’il existe toujours un nombre rationnel entre les deux, soit un nombre rationnel \(z\) tel que \(x<z\) et \(z<y\) (par exemple, \(z=x+y/2\)).

Cette propriété de l’ensemble \(\mathbb Q\) a fait qu’on a appelé autrefois cet ensemble le « continu du premier ordre » (voir par exemple Henri Poincaré, dans la Science et l’Hypothèse). L’idée est de différencier ce continu d’un continu du « second ordre », qui correspondrait précisément à l’ensemble \(\mathbb R\) des nombres réels. Cela signifie également que cette première idée ne fonctionne pas pour identifier l’ensemble \(\mathbb Q\).

1.2. Certaines grandeurs de la géométrie ne sont pas mesurables par des nombres rationnels

Revenons à l’exemple de la longueur de la diagonale du carré de côté \(1\) : cette longueur vaut \(\sqrt 2\), un nombre dont on peut montrer qu’il n’est pas rationnel, ce que savait déjà Pythagore et qui était à l’époque une tragédie pour sa philosophie, car certains rapports géométriques ne correspondaient pas à des nombres connus ! D’un autre côté, ce nombre est une solution de l’équation \(x^2-2=0\), puisque par définition le carré de \(\sqrt 2\) est \(2\). Il existe donc des équations avec des coefficients entiers ou rationnels, qui n’ont pas de solution dans \(\mathbb Q\) : on s’attend à ce que certaines de ces solutions soient des nombres réels, comme c’est le cas pour \(\sqrt 2\) : on peut en effet placer \(\sqrt 2\) sur l’échelle des grandeurs. D’autres nombres, comme \(\pi\), rapport du périmètre d’un cercle à son diamètre, doivent aussi représenter des grandeurs, mais ne sont même pas solutions d’une équation. Quoiqu’il en soit, il existe des « trous » dans l’ensemble \(\mathbb Q\), au sens où il « manque » des nombres pour mesurer certaines grandeurs, c’est-à-dire certains « nombres » qu’on peut situer par rapport à tous les nombres rationnels.

C’est au mathématicien français Augustin Louis Cauchy qu’on attribue une construction, peut-être la plus célèbre, des nombres réels à partir des nombres rationnels, c’est-à-dire une description utilisant l’ensemble \(\mathbb Q\) et les ressources de la théorie naïve des ensembles (voir Qu’est-ce qu’un ensemble ?). Cette construction – comme celle du mathématicien allemand Richard Dedekind – exploite cette idée des « trous » dans l’ensemble \(\mathbb Q\). Pour vous faire une idée de la perspective de Cauchy, découvrez comment nous revisitons ces concepts de manière axiomatique dans l’article consacré à [l’axiomatisation de la droite réelle] de notre encyclopédie MATHESIS::Essentiel.

 Pythagore

2. Boucher les trous avec Cauchy : construire les nombres réels

2.1. Des suites de nombres rationnels « aussi proches qu’on veut »

L’idée de la construction Cauchy est de considérer que les « trous » existant dans l’ensemble \(\mathbb Q\) peuvent être « approchés » indéfiniment par des suites de nombres rationnels, c’est-à-dire des listes infinies de nombres \(r_0,r_1,\ldots,r_n,\ldots\), indexées par les nombres entiers naturels. Il existe en effet des suites de nombres rationnels qui ont une limite, c’est-à-dire qui se « rapprochent indéfiniment » d’un certain nombre rationnel \(r\), au sens mathématique précis qu’on peut « s’approcher autant qu’on veut du nombre \(r\) » à condition de « se placer assez loin dans la suite »; cette idée trouve une formulation mathématique rigoureuse grâce à la théorie des ensembles. Par exemple, la suite \(1, \frac 1 2, \frac 1 3, \ldots,\frac 1 n,\ldots\) a pour limite le nombre \(0\). Or, il se trouve que ces suites, qu’on appelle convergentes, ont une autre propriété analogue : leurs termes sont « aussi proches l’un de l’autre qu’on veut » à condition de les choisir « assez loin dans la suite ». Cette propriété, dite « de Cauchy » peut également se formuler de manière rigoureuse, et si on note l’analogie évidente avec la propriété d’être une suite convergente, celle-ci est une propriété intrinsèque de la suite, ne faisant pas appel à un éventuel nombre « extérieur ».

2.2. Remplir les « trous » par des suites de Cauchy

Or, si toutes les suites convergentes, c’est-à-dire qui ont une limite dans l’ensemble \(\mathbb Q\), ont la propriété de Cauchy – l’inverse n’est pas toujours vrai : il existe des suites de Cauchy de nombres rationnels, qui ne possèdent pas de limite dans \(\mathbb Q\) ! L’ingéniosité de la construction de Cauchy consiste à considérer que les « trous » de l’ensemble \(\mathbb Q\) correspondent à des limites virtuelles de suites de Cauchy qui n’en ont pas… Autrement dit, on peut « représenter » ce qu’on entend par un « nombre réel » comme une limite d’une telle suite de Cauchy, qu’elle existe ou non. Stricto sensu, plusieurs suites de Cauchy peuvent intuitivement déterminer la même limite virtuelle, lorsque leurs termes respectifs se rapprochent indéfiniment, autrement dit lorsque la différence de leurs termes respectifs a pour limite 0 : on dit que deux telles suites sont équivalentes. Ainsi, on peut construire les nombres réels comme des ensembles de suites de Cauchy équivalentes, avec les seules ressources de la théorie des ensembles (et des nombres rationnels, laquelle repose sur la théorie des nombres entiers naturels).

2.3. On étend la « structure » de l’ensemble \(\mathbb Q\) à un ensemble \(\mathbb R\) de nombres réels

Dans cette approche, on peut représenter chaque nombre rationnel \(r\) comme un nombre réel : on le représente comme l’ensemble des suites équivalentes à la suite constante \(r,r,\ldots,r,\ldots\) ! Ainsi, on peut considérer que l’ensemble noté \(\mathbb R\) des nombres réels est une « extension » de l’ensemble \(\mathbb Q\) des nombres rationnels. Les opérations arithmétiques \(+\) et \(\times\) des nombres rationnels se prolongent à l’ensemble \(\mathbb R\), ainsi que la relation d’ordre \(<\) entre les nombres rationnels, ainsi que plusieurs autres propriétés. La démonstration de ces faits dépasse le cadre de cet article. L’ensemble \(\mathbb R\) possède en outre une propriété fondamentale que possède déjà l’ensemble \(\mathbb Q\), dite propriété d’Archimède : si \(x\) est un nombre réel, il existe toujours un nombre entier naturel \(n\) plus grand que \(x\), c’est-à-dire ayant la propriété que \(x<n\); cette propriété en apparence simple est essentielle à l’analyse réelle, c’est-à-dire l’étude des fonctions de nombres réels (fonctions polynomiales, racines, sinus, cosinus, exponentielle, logarithme…), de même que la propriété dite de la borne supérieure, qui n’est pas vraie dans l’ensemble \(\mathbb Q\) : tout sous-ensemble \(E\) de l’ensemble \(\mathbb R\), non vide et majoré (c’est-à-dire tel que tout élément de \(E\) est inférieur à un certain nombre réel, appelé majorant), possède une borne supérieure, c’est-à-dire un plus petit majorant. Cette propriété est analogue d’une propriété essentielle de l’ensemble \(\mathbb N\) des entiers naturels : toute partie non vide de \(\mathbb N\) possède un plus petit élément.

 A.L. Cauchy

Pour aller plus loin…

La construction des nombres réels est un voyage fascinant à travers les fondements de la mathématique. Si le sujet vous intéresse et vous souhaitez approfondir l’univers des nombres réels et leur axiomatisation, notre encyclopédie MATHESIS::Essentiel vous ouvre ses portes. Explorez l’article sur [l’axiomatisation de la droite réelle] pour une compréhension enrichissante :

3. La droite réelle est complète : il n’y a plus de trous

3.1. Les suites de Cauchy de nombres réels ont une limite

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :