Le produit scalaire de deux vecteurs dans un espace réel est un nombre réel qui tient compte de la direction, du sens et de l’amplitude des deux vecteurs.

1.Le produit scalaire naturel dans le plan euclidien

1.1.De la distance entre deux points au produit scalaire

Dans le plan euclidien \(\mathbb R^2\), la « distance (euclidienne) » dite « naturelle » entre deux points \(M=(a,b)\) et \(N=(c,d)\) est définie comme le nombre \(\sqrt{(a-c)^2+(b-d)^2}\). Cela vient de ce qu’on interprète cette longueur comme celle de l’hypoténuse d’un triangle rectangle, qu’on peut calculer grâce au théorème de Pythagore (voir Le Plan euclidien : géométrie antique et approche analytique). Par analogie, dans l’espace euclidien (à trois dimensions) \(\mathbb R^3\) on définit aussi la distance naturelle entre deux points \(A=(a,b,c)\) et \(B=(x,y,z)\) comme la racine carrée de la somme des carrés des différences des coordonnées. C’est donc le nombre réel \(d(A,B)=\sqrt{(a-x)^2+(b-y)^2+(c-z)^2}\). On peut grâce à cette définition définir par exemple une sphère de centre \(A=(a,b,c)\) et de rayon \(R\geq 0\) comme l’ensemble des points \(M=(x,y,z)\) de \(\mathbb R^3\) tels que \(d(A,M)=R\), ce qui se traduit par l’équation \((a-x)^2+(b-y)^2+(c-z)^2=R^2\).

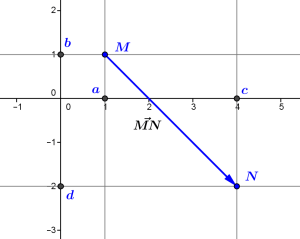
Si nous revenons au plan \(\mathbb R^2\), nous constatons que l’expression sous le signe \(\sqrt{}\) est de la forme \(x^2+y^2\) pour les nombres réels \(x=a-c\) et \(y=b-d\). Autrement dit, au lieu de considérer la distance comme associée aux deux points \(M\) et \(N\), on peut la considérer comme associée au vecteur \(\vec{MN}=(x,y)\in\mathbb R^2\) : c’est ce qu’on appelle la norme du vecteur \(\vec{MN}\), qu’on note \(||\vec{MN}||\). Cette norme, qui mesure l’amplitude d’un vecteur, est associée à une opération naturelle entre deux vecteurs \(\vec u=(x_1,y_1)\in\mathbb R^2\) et \(\vec v=(x_2,y_2)\in\mathbb R^2\), qu’on appelle produit scalaire de \(\vec u\) et \(\vec v\). Ce produit scalaire est défini comme le nombre réel \(\vec u.\vec v=x_1x_2+y_1y_2\), et on voit que la norme d’un vecteur \(\vec u=(x,y)\), soit la distance \(\sqrt{x^2+y^2}\) entre ses deux extrémités, est la racine carrée de son produit scalaire avec lui-même, c’est-à-dire \(\sqrt{\vec u.\vec u}\).

Sur la figure suivante, les coordonnées \((c-a,d-b)\) du vecteur \(\vec{MN}\) sont lisibles à partir des coordonnées des points \(M\) (\(a,b)\) et \(N\) (\(c,d)\). La norme du vecteur \(\vec{MN}\) est alors la distance entre \(M\) et \(N\), soit \(\sqrt{(c-a)^2+(d-b)^2}\).

1.2.Un vrai produit avec une signification géométrique

Pourquoi appelle-t-on cette opération un produit ? Parce que celui-ci possède des propriétés analogues au produit de deux nombres. Par exemple, si \(a,b,c\in\mathbb R\) sont trois nombres réels, on a la propriété bien connue de distributivité de la multiplication sur l’addition, soit l’égalité \(c\times (a+b)=c\times a+c\times b\). De même, pour \(\vec u=(a,b)\), \(\vec v=(x,y)\) et \(w=(z,t)\) trois vecteurs de \(\mathbb R^2\), on a \[\vec w.(\vec u+\vec v)=z\times (a+x)+t\times (b+y)=(za+tb)+(zx+ty)=(\vec w.\vec u)+(\vec w.\vec v).\] On voit que cette distributivité du produit scalaire sur l’addition des vecteurs provient en fait de la distributivé de \(\times\) sur \(+\) dans l’ensemble \(\mathbb R\). De la même manière, si \(a\) est un nombre réel, on peut facilement montrer que \(\vec u.(a\vec v)=(a\vec u).\vec v\), ce qui s’aparrente plutôt à la commutativité et l’associativité du produit de deux nombres. Notons aussi que le produit scalaire est symétrique, c’est-à-dire que \(\vec u.\vec v=\vec v.\vec u\).

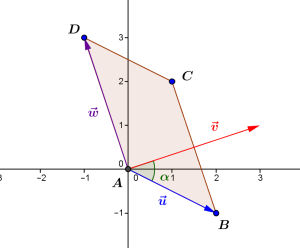
Dans le plan, le produit scalaire possède une interprétation géométrique indirecte. Si on considère l’angle (non orienté) \((\vec u,\vec v)\) formé par les vecteurs \(\vec u\) et \(\vec v\), on peut donner une expression trigonométrique du produit scalaire de \(\vec u\) et \(\vec v\) sous la forme \(\vec u.\vec v=||\vec u||\times ||\vec v||\times \cos (\vec u,\vec v)\). A partir de là, si on considère que deux vecteurs déterminent un parallélogramme, alors le produit scalaire \(\vec u.\vec v\) est l’aire signée (c’est-à-dire tenant compte du signe, soit un nombre positif ou négatif) du parallélogramme déterminé, non par les vecteurs \(\vec u\) et \(\vec v\), mais par \(\vec u\) et le vecteur \(\vec w\) obtenu en appliquant une rotation d’angle \(\pi/2\) (un quart de tour à gauche) au vecteur \(\vec v\). L’aire est signée parce que le cosinus de l’angle entre \(\vec u\) et \(\vec v\) est positif ou négatif, selon que l’angle (non orienté) est aigu (compris entre \(0\) et \(\pi/2\)) ou obtus (compris entre \(\pi/2\) et \(\pi\)).

Sur la figure suivante, on peut visualiser le produit scalaire \(\vec u.\vec v=||\vec u||\times ||\vec v||\times \cos\alpha\) des vecteurs \(\vec u\) et \(\vec v\) comme l’aire signée du parallélogramme \(ABCD\) construit à partir des vecteurs \(\vec u\) et \(\vec w\), où \(\vec w\) est obtenu à partir de \(\vec v\) par une rotation horaire d’angle \(\pi/2\), et où \(\alpha\) est l’angle entre \(\vec u\) et \(\vec v\). Le signe du produit scalaire est ici positif, car l’angle \(\alpha\) est aigu.

1.3.Une mesure de l’orthogonalité

Ainsi, le produit scalaire de deux vecteurs est un nombre réel qui combine à la fois le sens et la direction de deux vecteurs à travers l’angle qu’ils forment. Il peut donc servir de critère pour déterminer l’orthogonalité (analogue vectoriel de la perpendicularité) de deux vecteurs, et donc de deux droites par exemple. En ce sens, il est une « mesure » de l’orthogonalité de deux vecteurs, et permet même de définir lorsque deux vecteurs sont orthogonaux.

Deux vecteurs \(\vec u\) et \(\vec v\) sont, en effet, dits orthogonaux, par définition, lorsque l’angle (non orienté) qu’ils forment est un angle droit. En utilisant l’expression trigonométrique du produit scalaire \(\vec u.\vec v=||\vec u||\times ||\vec v||\times \cos (\vec u,\vec v)\), on voit que ce produit scalaire est nul exactement lorsque l’un des vecteurs \(\vec u\) ou \(\vec v\) est de norme nulle, ou bien lorsque \(\cos(\vec u,\vec v)=0\). Si donc aucun des vecteurs \(\vec u\) et \(\vec v\) ne sont nuls, leur produit scalaire est nul si, et seulement si, ils sont orthogonaux. Ceci permet, par exemple, de calculer directement l’équation d’une droite orthogonale à une droite donnée lorsqu’on connaît un vecteur directeur de celle-ci.

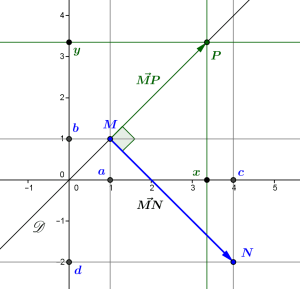
Sur la figure suivante, qui reprend la première, on montre comment le produit scalaire permet de trouver une équation cartésienne de la droite \(\mathscr D\) orthogonale au vecteur \(\vec{MN}\) en \(M\). Un point \(P\) de coordonnées \((x,y)\) est sur cette droite \(\mathscr D\) si et seulement si les vecteurs \(\vec{MN}\) et \(\vec{MP}\) sont orthogonaux, autrement dit si et seulement si \(\vec{MN}.\vec{MP}=0\), ou encore \((c-a)(x-a)+(d-b)(y-b)=0\). En développant, on obtient une équation cartésienne de \(\mathscr D\) de la forme \((c-a)x+(d-b)y-a(c-a)-b(d-b)=0\), dont les coefficients sont écrits à partir des coordonnées de \(M\) et de \(N\).

2.Produits scalaires en dimensions supérieures

2.1.Le produit scalaire naturel en dimension \(3\)

Pour aller plus loin