Les nombres entiers naturels ont deux visages : d’un côté, ils peuvent être vus comme des séquences ou des « énumérations » – ce qu’on appelle les nombres ordinaux. De l’autre, ils sont perçus comme des « quantités », ce qui nous mène aux nombres cardinaux. Bien que cette distinction ne soit pas toujours primordiale dans l’arithmétique classique, elle prend une importance cruciale lorsqu’on aborde les ensembles infinis. Car, étonnamment, avec l’infini une même quantité peut donner naissance à différents comptages. Pour une exploration rigoureuse du monde des nombres infinis, il devient impératif de séparer la discussion entre ordinaux et cardinaux. Dans cet article, nous plongerons d’abord dans l’univers fascinant des ordinaux, qui ont leur propre intérêt, et sont la base sur laquelle repose la définition des cardinaux.

1.Ordinaux et cardinaux : deux aspects distincts du nombre

1.1.Distinguer entre l’ordre et la quantité

Il existe deux manières bien différentes de considérer les nombres entiers naturels. Ils servent soit à énumérer les objets d’un ensemble fini (on insiste alors plutôt sur l’ordre dans lequel ils sont rangés), soit à compter la quantité d’objets d’un tel ensemble (on insiste alors plutôt sur la « puissance » numérique qu’ils représentent). Dans le premier cas, on parle de nombre ordinal, dans le second cas de nombre cardinal. Dans les signes du langage naturel, les deux notions sont bien différenciées : on parle d’adjectif numéral ordinal (premier, deuxième, troisième…) ou d’adjectif numéral cardinal (un, deux, trois…). Mais en mathématique, où l’on s’intéresse d’abord à la réalité du nombre plutôt qu’aux signes qui la décrivent, les deux notions se confondent en ce qui concerne les nombres finis, c’est-à-dire les nombres entiers naturels. Cela provient de ce que quel que soit l’ordre dans lequel on compte les objets d’un ensemble fini, on obtient le même résultat.

1.2.Deux types de nombres pour l’infini

Cependant, l’ordre associé à une certaine énumération contient une information supplémentaire à la quantité d’objets, puisqu’on peut précisément, en général, ranger les éléments d’un même ensemble fini dans des ordres différents. Or, cette possibilité de compter, ou d’énumérer les ensembles finis, s’étend naturellement à tous les ensembles, et donc aux ensembles infinis, grâce à l’axiome du choix de la théorie des ensembles. Mais lorsqu’on énumère un ensemble infini, on peut aboutir à des résultats différents ! C’est pourquoi il faut distinguer, parmi les nombres infinis, qu’on dit aussi « transfinis », les nombres ordinaux et les nombres cardinaux, les seconds étant des cas (bien) particuliers des premiers. Nous abordons ici la notion de nombre ordinal, fini ou infini, telle qu’on la conçoit dans la théorie des ensembles, et ceci sans logique formelle, mais grâce à la théorie des classes (voir Le paradoxe de Russell et la théorie des classes).

2.Ensembles bien ordonnés

2.1.Ordres linéaires

Que signifie qu’on peut « énumérer » des ensembles infinis ? La notion d’ordinal permet elle-même de préciser ce qu’on entend par là, mais à l’origine, dans les travaux de Cantor il s’agit d’ordonner les éléments d’un ensemble, fini ou infini, d’une certaine manière assurant qu’on dispose toujours d’un plus petit élément et qu’on peut toujours comparer les énumérations. Rappelons qu’un ordre linéaire sur un ensemble $E$ est une relation binaire, qu’on note souvent $<$, et qui possède les propriétés usuelles de l’ordre strict :
i) Pour aucun élément $x$ de $E$ on ne peut avoir $x<x$ (anti-réflexivité)
ii) Si $x,y,z$ sont deux éléments de $E$ tels que $x<y$ et $y<z$, alors $x<z$ (transitivité)
iii) Si $x,y$ sont deux éléments de $E$, on a soit $x<y$, soit $x=y$, soit $x>y$ (totalité).
Par exemple, l’ordre strict sur l’ensemble $\mathbb N$ des entiers naturels, ou sur l’ensemble $\mathbb R$ des nombres réels, sont des ordres linéaires.

2.2.Bons ordres

Il existe toutefois une différence fondamentale entre les ordres linéaires sur $\mathbb N$ et sur $\mathbb R$ : dans le premier cas, on a un plus petit élément, ce qui est aussi le cas de toute partie non vide de $\mathbb N$, ce qu’on peut démontrer à partir des axiomes de Peano. Dans le cas de $\mathbb R$, cette propriété est prise en défaut : par exemple, l’ensemble $\mathbb R_+^*$ des réels strictement positifs ne possède pas de plus petit élément ! Or, cette propriété distinctive de $\mathbb N$ est aussi vérifiée pour ses segments initiaux, c’est-à-dire les sous-ensembles de la forme $[[0,n[[=\{i\in \mathbb N: i<n\}$ pour $n$ un entier naturel (étant entendu que pour $n=0$, $[[0,0[[=\emptyset$ est l’ensemble vide). C’est ce concept qui sert de modèle pour la notion « d’énumération » :

Définition 1
Un bon ordre sur un ensemble $E$ est une relation d’ordre linéaire $<$ sur $E$, telle que toute partie non vide de $E$ possède un plus petit élément pour $<$.

Ainsi, dans l’ancienne théorie des ensembles, une énumération d’un ensemble $E$ quelconque, fini ou infini, consiste en une façon d’ordonner ses éléments en un bon ordre.

Exemple 1
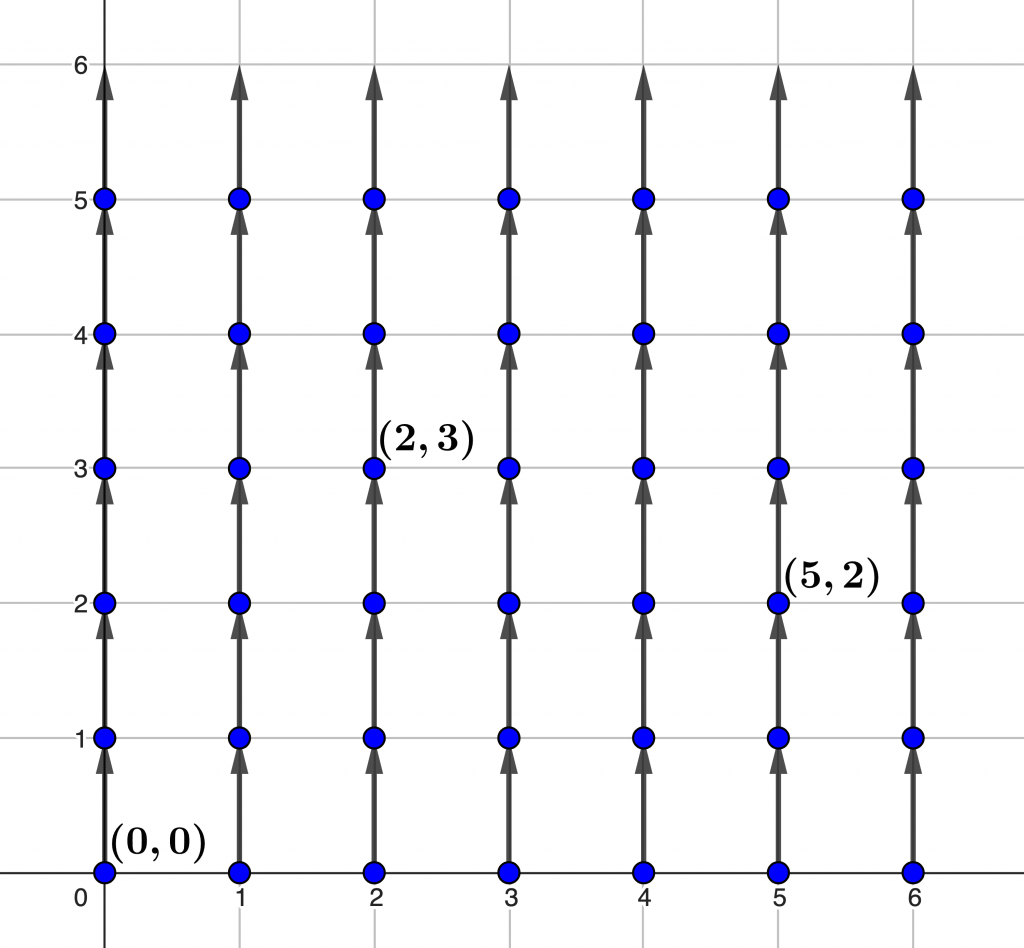
Sur le produit cartésien $\mathbb N^2=\mathbb N\times \mathbb N$, on définit un bon ordre en ordonnant les couples $(n,m)$ d’entiers naturels selon l’ordre dit lexicographique (l’ordre « du dictionnaire ») : on dit que $(n,m)<(n’,m’)$ si $n<n’$, ou bien si $n=n’$ et $m<m’$. De cette manière, toute partie non vide $S$ de $\mathbb N^2$ possède un plus petit élément : il suffit pour cela de choisir le plus petit entier $n$ figurant dans un couple de la forme $(n,m)\in S$, puis de choisir le plus petit entier $m$ figurant dans un tel couple, pour ce choix de $n$. Dans l’ordre lexicographique, les couples d’entiers naturels sont ordonnés comme suit : $(0,0),(0,1),(0,2),\ldots,(0,n),\ldots,(1,0),(1,1),(1,2),\ldots,(1,n),\ldots,
(2,0),(2,1),(2,2),\ldots,(2,n),\ldots,(m,n),\ldots$.

2.3.L’existence d’une énumération

Une telle énumération est-elle toujours possible ? Il s’agit d’un théorème de la théorie des ensembles, qui est en fait équivalent à l’axiome du choix :

Théorème 1
Sur tout ensemble $E$ il existe une relation de bon ordre.

Autrement dit, il est toujours possible de « ranger » les éléments d’un ensemble quelconque sous la forme d’une énumération. Les segments initiaux $[[0,n[[$ de $\mathbb N$ sont naturellement rangés par l’ordre strict (même l’ensemble vide, ce dont il faut se convaincre à partir de la définition d’un bon ordre !), mais l’ensemble $\mathbb N$ lui-même aussi est ainsi rangé. Or, si on considère chaque ensemble $[[0,n[[$ comme une version « ordinale » du nombre $n$ (il contient $n$ éléments !), par analogie l’ensemble $\mathbb N$ est formé de tous les nombres « ordinaux » strictement inférieurs « à l’infini ». En d’autres termes, l’ensemble $\mathbb N$ lui-même apparaît comme une sorte de nombre (ordinal) infini, ce à quoi nous allons donner un sens précis et rigoureux.

3.Ordinaux de von Neumann

3.1.Les ordinaux comme types de bons ordres

De la même manière que deux ensembles ont « le même nombre d’éléments » lorsqu’il existe une bijection entre eux, et que ce nombre d’éléments est ce qu’on appelle leur « cardinal », deux ensembles bien ordonnés $(E_1,<_1)$ et $(E_2,<_2)$ auront « le même type d’ordre » lorsqu’il existera une bijection strictement croissante entre $E_1$ et $E_2$, c’est-à-dire une bijection $f:E_1\cong E_2$ telle que pour tous $x,y\in E_1$, on ait $x<y$ si et seulement si $f(x)<f(y)$. Deux ensembles bien ordonnés ayant le même type d’ordre sont en effet indiscernables, et devraient être identifiés, c’est-à-dire correspondre au même nombre ordinal. La définition initiale d’un ordinal, c’est donc celle d’un « type de bon ordre » au sens suivant :

Définition 2
Un nombre ordinal est une classe $O$ non vide d’ensembles bien ordonnés, ayant tous le même type d’ordre, et telle que tout ensemble bien ordonné ayant le même type d’ordre qu’un élément de $O$, est dans $O$.

Autrement dit, l’idée originale de Cantor était de définir un ordinal comme « type de bon ordre » par le truchement de la classe de tous les bons ordres qui peuvent le représenter, indépendemment donc de la représentation choisie.

Exemple 2
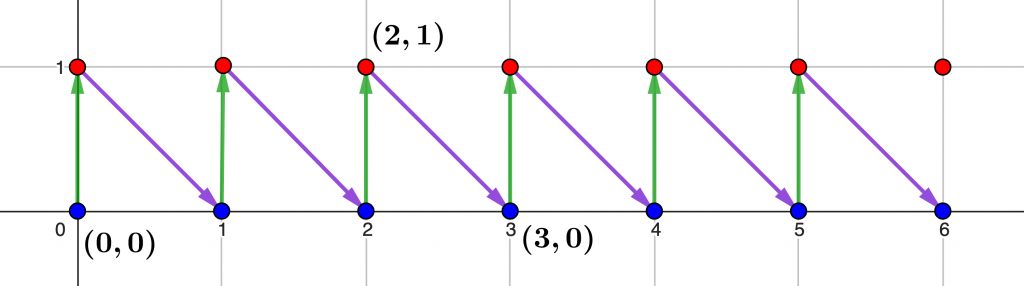
Comme dans l’exemple 1, on peut ordonner les éléments de l’ensemble $\mathbb N\times \{0,1\}$ de manière lexicographique, en décrétant que $0<1$ sur la deuxième composante : cela signifie que les couples sont rangés comme suit : $(0,0),(0,1),(1,0),(1,1),(2,0),(2,1),\ldots$ et on montre facilement que c’est le même type d’ordre que l’ordre linéaire naturel sur $\mathbb N$ : ils définissent donc tous deux le même ordinal. Mais on peut aussi définir un bon ordre sur $\mathbb N\times \{0,1\}$ en décrétant que viennent en premier tous les couples de la forme $(n,0)$, puis seulement ensuite tous ceux de la forme $(n,1)$, c’est-à-dire $(0,0),(1,0),(2,0),\ldots,(n,0),\ldots,(0,1),(1,1),(2,1),\ldots,(n,1),\ldots$ : le bon ordre obtenu équivaut alors à « deux copies de $\mathbb N$ mises bout-à-bout ». Dans ce cas, tout élément de la forme $(n,0)$ est strictement inférieur à $(0,1)$, qui apparaît alors comme un élément « infini » : ce phénomène n’apparaît pas avec les entiers, donc ce type d’ordre n’est pas celui de $\mathbb N$, et définit un autre nombre ordinal !

3.2.Les ordinaux de von Neumann

Cette manière de procéder par relation d’équivalence convient bien aussi à la définition du nombre cardinal (c’est celle qu’adopte essentiellement Gottlob Frege dans ses Fondements de l’Arithmétique), mais elle ne nous donne pas un ordinal comme un « nombre » au sens d’un objet mathématique manipulable comme tel, à moins que ces classes ne soient des ensembles véritables, ce qui n’est pas le cas. On doit à John von Neumann une description des nombres ordinaux non comme « classes de types de bons ordres », mais comme certains bons ordres très particuliers qui représentent chacune d’entre elle, et peuvent donc les remplacer utilement pour les manipuler, et notamment calculer avec eux. On appelle ainsi ordinaux de von Neumann certains ensembles qui servent de généralisation ordinale aux entiers naturels dans la théorie des ensembles, et servent à compter de manière standard tous les ensembles, finis ou infinis. Puisqu’ils servent à représenter les ordinaux en théorie axiomatique des ensembles, ils tendent à remplacer les ordinaux cantoriens et à être appelés simplement « ordinaux ».

3.3.Les entiers naturels comme ordinaux

Cette description des ordinaux comme ensembles repose sur une idée formidable dans sa simplicité, et qui consiste essentiellement en deux choses :
i) S’inspirer de l’interprétation ordinale, déjà évoquée ici, de chaque entier naturel $n$ comme l’ensemble des entiers naturels $i<n$, c’est-à-dire le segment initial $[[0,n[[$
ii) Généraliser l’intuition que l’ensemble $\mathbb N$ lui-même est une sorte de « nombre ordinal infini » composé de tous ceux qui lui sont strictement inférieurs, et obtenu comme « limite » par leur réunion ensembliste.

Ainsi, le premier nombre ordinal doit être celui qui représente l’entier $0$, c’est-à-dire l’ensemble vide $\emptyset=[[0,0[[$. Or, puisqu’on a représenté $0$ comme $\mathbf 0=\emptyset$, il faut désormais représenter $1$, non plus comme $[[0,1[[=\{0\}$, mais comme $\mathbf 1=\{\emptyset\}$, qu’on doit distinguer du précédent, puisqu’il contient un élément ! On continue avec $\mathbf 2=\{\mathbf 0,\mathbf 1\}=\{\emptyset,\{\emptyset\}\}$, et on procède ainsi pour chaque entier naturel $n$, qui se trouve alors représenté comme l’ensemble $\mathbf n$ des ordinaux qui lui sont strictement inférieurs, et on passe de la représentation de $n$ à celle de $n+1$ par l’opération appelée « successeur », définie pour les ordinaux comme $\mathbf{n+1}=s(\mathbf n)=\mathbf n\cup \{\mathbf n\}$. Ainsi, à partir de l’ensemble vide et d’opérations ensemblistes élémentaires (la paire et la réunion), on peut générer une représentation de tous les entiers naturels.

3.4.Les ordinaux comme ensembles

De cette manière, on peut représenter l’ensemble $\mathbb N$ comme la classe (en fait l’ensemble, si on admet l’existence de $\mathbb N$) notée $\omega$ (« omega », dernière lettre de l’alphabet grec) des représentations $\mathbf n$ des entiers naturels $n$, et il apparaît que pour tout entier $n$, on a $\mathbf n=\{\mathbf i : i<n\}$. Mais $\omega$, ainsi défini, possède une propriété étrange : il est aussi bien la réunion des ensembles $\mathbf n$ que l’ensemble de tous ces ensembles ! Les ensembles de la forme $\mathbf n$, ainsi que $\omega$, ont cette propriété contre-intuitive mais ubiquitaire en théorie des ensembles : chacun de leurs éléments en est aussi un sous-ensemble, et on dit qu’ils sont transitifs. Cette « transitivité » est en fait celle de la relation d’appartenance $\in$ entre ensembles, et qui est devenue elle-même la représentation de la relation naturelle de bon ordre strict entre les entiers naturels ! Au prix d’une construction d’un formalisme extrême, on aboutit ainsi à la définition rigoureuse des ordinaux de von Neumann :

Définition 3
Un ordinal (de von Neumann) est un ensemble transitif $O$, pour lequel la relation d’appartenance $\in$ entre éléments est un bon ordre.

Avec cette notion d’ordinal, nous avons finalement un objet mathématique propre comme ensemble véritable, susceptible de manipulations dans la théorie des ensembles, et qui permet de « compter » les éléments de tout ensemble, fini ou infini. On démontre en effet que chaque « classe de type de bons ordres » (chaque ordinal au sens de Cantor) contient alors un et un seul ordinal (au sens de von Neumann) qui le représente. Mais il est toujours possible d’obtenir des résultats différents, selon la manière dont on énumère les ensembles infinis ! Notons que tous les éléments d’un ordinal… sont eux-mêmes des ordinaux : cela découle immédiatement de la définition.

4.Le paradoxe de Burali-Forti

4.1.Les trois types d’ordinaux

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :