L’approche mathématique de la physique s’initie souvent par la description du mouvement. Cette démarche s’appuie sur la conceptualisation du mouvement en tant que variation de position en fonction du temps, ce qui conduit à sa modélisation comme une fonction temporelle dans un espace euclidien. Cette modélisation est rendue possible grâce à la théorie des nombres réels, de l’espace euclidien et des fonctions à variable réelle. Par ailleurs, les dérivées première et seconde de la « loi » du mouvement qu’est la fonction nous renseignent sur les paramètres cinématiques fondamentaux que sont la vitesse et l’accélération, toutes deux envisagées ici sous un angle vectoriel.

1.Mouvement d’un corps et description fonctionnelle

1.1.Une représentation du mouvement pour la physique

On dit qu’un corps en déplacement dans l’espace suit une trajectoire. La représentation physique d’une telle situation passe par son interprétation mathématique, possible grâce à la théorie des nombres réels, via la théorie des fonctions de l’analyse réelle et de l’espace euclidien. Il s’agit alors de s’appuyer sur une description idéalisée de la position du corps en fonction du temps.

Afin de simplifier le problème, on réduit cette description à celle d’un seul point mobile $M=(x,y,z)$ de l’espace euclidien $\mathbb R^3$ (ensemble de tous les triplets $(a,b,c)$ de nombres réels), par exemple le centre de gravité du corps (le cas d’un mouvement dans le plan euclidien $\mathbb R^2$ est bien sûr analogue et plus simple). Les instants du mouvement considéré sont alors représentés par les éléments d’un intervalle réel $I$, et à chaque instant $t\in I$ la position du corps est repérée par un point $M$ qui dépend de $t$.

1.2.La description mathématique du mouvement

Ainsi, la position $M$ du corps $K$ dépend de l’instant $t$, de sorte qu’on la considère comme une fonction $f$ de $I$ dans l’espace $\mathbb R^3$, qui associe à chaque instant $t\in I$ la position $f(t)=(x(t),y(t),z(t))$ du point représentant le corps K à l’instant $t$ : cette fonction est en quelque sorte la « loi » du mouvement, dont on peut tirer de nombreuses informations lorsqu’elle revêt une forme mathématique connue.

La description mathématique du mouvement esquissée ici en est une interprétation, qui repose sur trois éléments fondamentaux et étroitement associés :

1. L’intuition que le mouvement est un changement de position du corps dans « l’espace » avec le « temps »
2. Une interprétation de l’espace et du temps de l’intuition, c’est-à-dire de l’expérience, par des représentations géométriques utilisant les nombres réels
3. Une association entre l’espace et le temps de l’expérience et leurs représentations mathématiques par le principe de la mesure des longueurs et des durées.

2.Vitesse associée à la représentation du mouvement

2.1.Fonctions coordonnées et application des concepts mathématiques

L’interprétation mathématique du mouvement d’un corps $K$ dans l’espace par une fonction $f:I\to \mathbb R^3$ nous impose de considérer les fonctions coordonnées de $f$. En effet, pour tout instant $t\in I$ le point $f(t)$ de $\mathbb R^3$ repérant la position de $K$ possède trois coordonnées $x(t),y(t)$ et $z(t)$, et chacune des fonctions $x,y,z$ définies ainsi sur le même intervalle $I$ prennent leurs valeurs dans $\mathbb R$ : ce sont les fonctions coordonnées de $f$.

Cette description nous permet désormais d’appliquer les concepts mathématiques de l’analyse réelle, et notamment le calcul différentiel, pour interpréter certaines caractéristiques du mouvement représenté à travers la fonction $f$.

2.2.Vitesse moyenne entre deux instants

L’intuition nous suggère par exemple que la vitesse associée au mouvement est un rapport de grandeurs : celui de la distance parcourue par le corps entre deux instants, à la durée qui sépare ces deux instants ; ainsi associe-t-on dans l’expérience l’espace et le temps.

Or, si l’on mesure la durée et les distances par des nombres réels, la vitesse peut donc s’exprimer comme un rapport entre nombre réels, et donc comme un objet mathématique bien défini. Ceci étant dit, la vitesse est d’abord mesurée comme un rapport moyen : en mesurant la distance euclidienne séparant deux positions $f(t_1)$ et $f(t_2)$ du corps K aux instants $t_1$ et $t_2$, on obtient la vitesse moyenne entre $t_1$ et $t_2$ comme le rapport numérique ${||f(t_2)-f(t_1)||}{|t_2-t_1|}$, où ici $||.||$ est la norme euclidienne (on rappelle que si $u=(x,y,z)\in\mathbb R^3$, par définition on a $||u||=\sqrt{x^2+y^2+z^2}$).

Autrement dit, par définition on a $||f(t_1)-f(t_2)||=\sqrt{[x(t_1)-x(t_2)]^2+[(y(t_1)-y(t_2)]^2+[(z(t_1)-z(t_2)]^2}$, ce qui nous donne une expression analytique complète de la vitesse moyenne en divisant par la durée $|t_1-t_2|$.

2.3.Vitesse vectorielle

L’expression analytique de la vitesse moyenne entre deux instants (ou deux points) fait apparaître un calcul de norme euclidienne procédant à partir de données de la fonction $f$ : les valeurs de celle-ci, et plus précisément de ses fonctions coordonnées, aux instants $t_1$ et $t_2$. Il s’agit, sur le plan mathématique, de calculer la distance euclidienne entre deux positions distinctes du mouvement, représentées respectivement par les points $M_1:=f(t_1)=(x(t_1),y(t_1),z(t_1))$ et $M_1:=f(t_1)=(x(t_1),y(t_1),z(t_1))$ de l’espace $\mathbb R^3$.

Autrement dit, on calcule avec la vitesse moyenne entre $t_1$ et $t_2$ la norme du vecteur $\vec{M_1M_2}$, qui représente le changement de position ou déplacement du corps entre les instants $t_1$ et $t_2$. La donnée de la fonction $f$ comme représentation du mouvement de $K$ contient donc plus d’information que la seule distance., et la vitesse peut ainsi être conçue plutôt comme variation de la position du corps en fonction du temps. Une telle vitesse est vectorielle, puisqu’elle est désormais exprimée comme rapport d’un changement de position à une durée : il s’agit de la grandeur $\dfrac{f(t_2)-f(t_1)}{t_2-t_1},$ définie seulement comme précédemment pour $t_1\neq t_2$, qui est bien un vecteur de l’espace, de coordonnées $\left(\dfrac{x(t_2)-x(t_1)}{t_2-t_1},\dfrac{y(t_2)-y(t_1)}{t_2-t_1},\dfrac{z(t_2)-z(t_1)}{t_2-t_1}\right)$, et dont la norme est la vitesse moyenne calculée précédemment.

2.4.Vitesse instantannée

On reconnaît, dans le rapport $\dfrac{f(t_2)-f(t_1)}{t_2-t_1}$ qui représente la vitesse vectorielle moyenne du mouvement décrit par $f$ entre $t_1$ et $t_2$, l’analogue spatial d’un rapport de monotonie, c’est-à-dire d’un rapport d’accroissement de la fonction. Ce rapport étant un vecteur, il possède trois coordonnées $\dfrac{x(t_2)-x(t_1)}{t_2-t_1},\dfrac{y(t_2)-y(t_1)}{t_2-t_1},\dfrac{z(t_2)-z(t_1)}{t_2-t_1},$ chacune d’entre elle étant un rapport de monotonie pour une des fonctions coordonnées $x(t),t(y),z(t)$ de $f(t)$ entre les instants $t_1$ et $t_2$.

Considérons $t_1$ comme une valeur fixe, un instant de référence auquel on voudrait calculer une vitesse « instantanée » : en désignant par $t$ un instant variable remplaçant l’instant fixe $t_2$ dans les expressions précédentes, inférieur ou supérieur à $t_1$, une telle vitesse serait la limite de la fonction $\dfrac{f(t)-f(t_1)}{t-t_1}$ lorsque $t$ tend vers $t_1$, autrement dit le vecteur $f'(t_1)$, c’est-à-dire la dérivée de la fonction $f$ au point $t_1$, si l’on suppose que cette dérivée est calculable (ce qui revient à choisir comme description pour $f$ une fonction dérivable e, $t_1$).

Définition 1
La vitesse instantanée du mouvement représenté par la fonction $f$ à l’instant $t_1$ est la dérivée de la fonction $f$ en $t_1$, c’est-à-dire le vecteur $f'(t_1)$.

Les coordonnées de ce vecteur « vitesse instantanée » sont, par définition, les dérivées de chaque fonction coordonnée de $f$ au point $t_1$, soit $f'(t_1)=(x'(t_1),y'(t_1),z'(t_1))$.

Ainsi, la notion intuitive de vitesse instantanée du mouvement d’un corps est naturellement représentée sur le plan mathématique par la dérivée de la fonction qui représente ce mouvement. On a également une notion de vitesse numérique instantanée, qui doit être par analogie la limite du rapport numérique $\dfrac{||f(t)-f(t_1)||}{|t-t_1|}$ lorsque $t$ tend vers $t_1$, autrement dit la limite de $||\dfrac{f(t)-f(t_1)}{t-t_1}||$, vitesse numérique moyenne entre $t_1$ et $t_2$, lorsque $t$ tend vers $t_1$ : par continuité de la norme euclidienne, cette limite est précisément la norme de la vitesse vectorielle instantanée, c’est-à-dire $||f'(t_1)||$.

3.Représentation géométrique du mouvement

Sur le plan géométrique, le mouvement représenté par la fonction $f$ décrit une courbe $C$ dans l’espace euclidien, dont le graphe (c’est-à-dire l’ensemble des couples $(t,f(t))$) est donc un sous-ensemble $G$ de $\mathbb R\times\mathbb R^3$. En général, il est possible que la courbe possède des auto-intersections, autrement dit qu’elle passe par un même point à deux instants différents. Dans ce cas, la courbe comme sous-ensemble de l’espace (c’est-à-dire l’image de la fonction $f$) ne contient pas toute l’information du mouvement, et il faut faire l’étude géométrique de celui-ci à partir de son graphe.

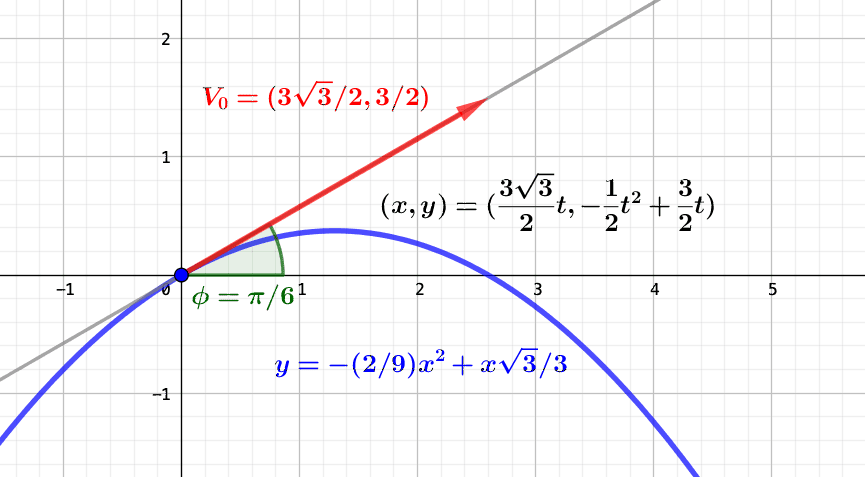
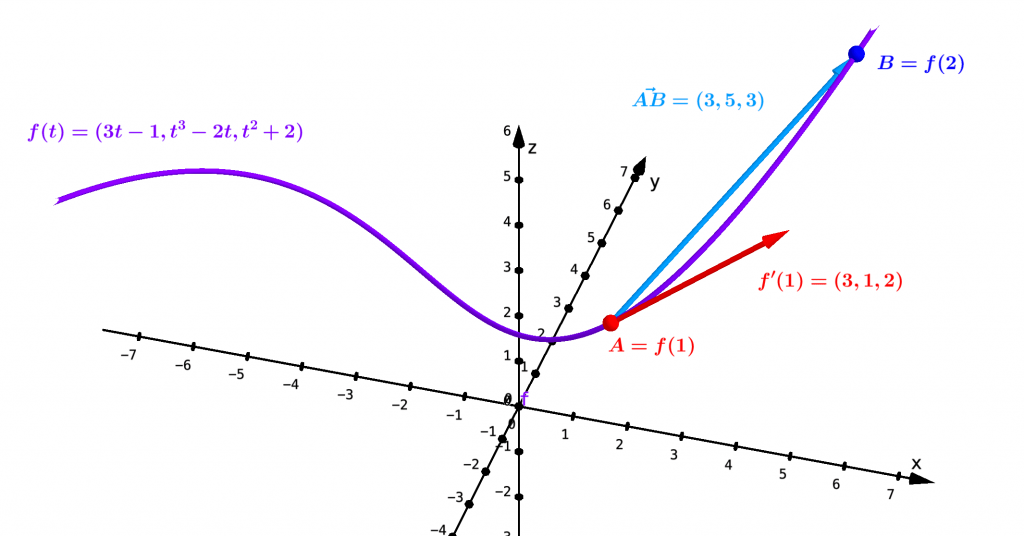
Si toutefois la fonction $f$ est injective, on peut identifier le graphe $G$ à la courbe $C$. Dans ce cas, à un instant $t_1$ donné correspond un unique point $f(t_1)$ de la courbe géométrique : la vitesse (vectorielle) instantanée du mouvement, c’est-à-dire maintenant la dérivée $f’(t_1)=(x'(t_1),y'(t_1),z'(t_1))$ de la fonction $f$ au point $t_1$, s’interprète comme un vecteur directeur de la tangente à la courbe $C$ au point $f(t_1)$. Ainsi, la vitesse vectorielle instantanée décrit à la fois la direction et l’amplitude du mouvement à l’instant $t_1$.

4.L’accélération comme modification des caractéristiques du mouvement

4.1.Accélération moyenne entre deux instants