Les nombres entiers naturels premiers sont sont ceux qui n’ont pas d’autres diviseurs que 1 et eux-mêmes. Ils existent en nombre infini par le théorème d’Euclide, qui n’est pas difficile à démontrer.

Les nombres premiers

Diviseurs et nombres premiers

Un nombre premier est un nombre entier naturel non nul (voir Qu’est-ce qu’un nombre entier naturel ? Définir ou axiomatiser) \(p\) différent de \(1\) dont les seuls diviseurs sont \(1\) et \(p\) lui-même. Mais qu’est-ce qu’un diviseur ? Un diviseur d’un nombre entier naturel \(n\) est un entier naturel \(d\) tel que \(d\) divise \(n\)… c’est-à-dire tel que \(n\) est un multiple de \(d\). Autrement dit, un diviseur \(d\) d’un entier naturel \(n\) est un nombre possédant la propriété que « \(d\) multiplié par un certain nombre \(k\) vaut \(n\) ». Mathématiquement, cela s’exprime rigoureusement par « il existe un entier naturel \(k\) tel que \(n=d\times k\) ». Un nombre premier, c’est donc un nombre entier naturel non \(p\neq 1\) pour lequel il n’existe pas d’autre décomposition de \(p\) sous la forme d’un produit \(d\times k\), que les décompositions dites « triviales » que sont \(p=1\times p\) et \(p=p\times 1\).

Tester si un nombre est premier

Parmi les premiers nombres premiers, on pourrait citer \(2\), \(3\), \(5\), \(7\), \(11\), \(13\), \(17\), \(19\)… Pour savoir que ces nombres sont premiers, il faut pouvoir le démontrer; c’est possible en effectuant par exemple des divisions euclidiennes. En général, il existe un critère pour tester si un nombre \(n\) est premier : s’il n’est pas premier, il existe un diviseur de \(n\) qui est un nombre premier \(p\) (ce qu’on appelle un facteur premier) et qui est inférieur à \(\sqrt n\). Par savoir si un nombre \(n\) donné est premier, il suffit donc de tester sa divisibilité par tous les nombres premiers \(p\) déjà connus et inférieurs à \(\sqrt n\). Si aucun de ceux-ci ne divise \(n\), alors \(n\) est premier ! Par exemple, pour savoir si \(97\) est premier, on remarque que \(9^2=81<97<10^2=100\), donc \(9<\sqrt{97}<10\) : on teste les nombres premiers entre \(1\) et \(9\), soit \(2,3,5\) et \(7\) et aucun ne divise \(97\) : celui-ci est donc premier.

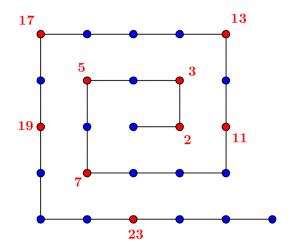
Les neuf premiers nombres premiers tels qu’ils se répartissent sur la spirale d’Ulam.

Le théorème d’Euclide

L’ensemble des nombres premiers est infini

Il semble qu’on puisse toujours, étant donné un nombre premier \(p\) donné, trouver un  nombre premier strictement plus grand que \(p\). C’est en fait une conséquence d’un célèbre théorème de l’Antiquité, qu’on trouve dans les Eléments d’Euclide, et qui énonce qu’il existe toujours plus de nombres premiers qu’un ensemble (fini) de nombres premiers donnés. Dans le langage de la mathématique moderne, on dirait qu’il existe une infinité de nombres premiers, ou encore que l’ensemble des nombres premiers est infini. Cela signifie qu’il n’est pas possible de les « compter », c’est-à-dire de trouver un nombre entier naturel \(n\) qui permette de les écrire comme une liste \(p_1,p_2,\ldots,p_n\) (voir Le fini et l’infini mathématiques : comparer et dénombrer).

Démontrer le théorème d’Euclide

Ce théorème n’est pas très difficile à démontrer, et nous proposons ici un schéma de la démonstration. Il nous faut en prérequis admettre trois faits arithmétiques simples :

• Fait 1 : tout nombre entier \(n\geq 2\) possède un facteur premier (un diviseur qui est un nombre premier)
• Fait 2 : si \(a,b,c\) sont trois entiers naturels tels que \(a\leq b\), \(c\neq 0\) et \(c\) divise \(a\) et \(b\), alors \(c\) divise \(b-a\) (dans ce contexte, le nombre entier naturel \(x\) tel que \(a+x=b\))
• Fait 3 : si \(d\) est un diviseur d’un entier non nul \(n\), alors \(d\leq n\).

A partir de la définition du produit de \(n\) nombres par récurrence, la démonstration du théorème peut se faire selon le schéma suivant :

• On raisonne par l’absurde en supposant qu’il n’y a qu’un nombre fini de nombres premiers, \(p_1,\ldots,p_n\)
• On considère le nombre \(m=p_1\times \ldots\times p_n+1\), qui est plus grand que \(2\) et possède donc par le Fait 1 un facteur premier \(q\), qui est forcément l’un des \(p_i\)
• Alors, \(q\) est à la fois un diviseur du produit \(p_1\times \ldots\times p_n\) des \(p_i\) et de \(m\), donc \(q\) divise \(1=m-p_1\times \ldots\times p_n\) par le Fait 2
• Par le Fait 3, on a alors \(q\leq 1\) mais par définition, le nombre premier \(q\) est supérieur à \(2\), donc on obtient \(2\leq 1\), ce qui est une contradiction !
• Par reductio ad absurdum (réduction à l’absurde), on en déduit que l’hypothèse de départ est fausse, autrement dit que l’ensemble des nombres premiers est infini.

Corollaire : les nombres premiers sont « cofinaux » dans l’ensemble \(\mathbb N\)

Du théorème d’Euclide, on peut déduire une propriété plus « visuelle » de l’infinité des nombres premiers : quel que soit l’entier naturel \(n\), on peut toujours trouver un nombre premier \(p\) « strictement plus grand que \(n\) », c’est-à-dire tel que \(n<p\). En fait, les sous-ensembles infinis de \(\mathbb N\) sont exactement ceux qui possèdent cette propriété, ce qu’on peut démontrer avec des méthodes élémentaires de théorie des ensembles.

Retrouvez l’article en  vidéo sur MATHESIS, la chaîne YouTube :

Pour aller plus loin

• La théorie des nombres premiers est fondamentale dans l’arithmétique ou théorie des nombres. Découvrez une approche élémentaire et rigoureuse dans le cours numéro 3 du semestre I de MATHESIS :

Mathesis I.3 : Arithmétique Elémentaire (Des nombres entiers naturels aux nombres rationnels)

• La  théorie de l’infini mathématique est accessible de manière rigoureuse à partir de notions élémentaires de théorie des ensembles et de logique mathématique. Découvrez la théorie des ensembles finis et infinis dans le cours numéro 2 du semestre I de MATHESIS :

Mathesis 1.2 : Ensembles, Applications et Numération (Du fini à l’infini mathématique)