Les propriétés des polynômes à une indéterminée sur un corps sont analogues à celles des nombres entiers relatifs. En exploitant cette analogie à partir de la notion de polynôme irréductible, on en tirer des informations précieuses sur l’arithmétique des polynômes, et donc sur les propriétés des fonctions polynomiales. Nous revenons sur la décomposition des polynômes en facteurs irréductibles, analogue à la décomposition des entiers en nombres premiers, et nous en tirons des conclusions sur les racines de certains polynômes. En particulier, les polynômes à coefficients réels et complexes s’étudient à travers le prisme d’une propriété analytique des polynômes réels, et le théorème fondamental de l’algèbre, qui en découle, énonce que tout polynôme complexe se décompose en facteurs linéaires. Nous retrouvons l’analyse classique des polynômes quadratiques réels à partir de leur discriminant, lequel nous permet d’aboutir à la classification des polynômes irréductibles à coefficients réels.

1.L’arithmétique des polynômes à coefficients dans un corps

Les polynômes à une indéterminée et à coefficients dans un anneau $A$ sont une formalisation mathématique des équations polynomiales. En tant qu’objets mathématiques, on peut leur appliquer la théorie des anneaux, puisque l’ensemble $A[X]$ de ces polynômes forme lui-même un anneau. En particulier, si $K$ est un corps (tout élément non nul est inversible), l’anneau $K[X]$ des polynômes à coefficients dans $K$ est un anneau dit factoriel, c’est-à-dire possédant des propriétés arithmétiques analogues à celle de l’ensemble $\mathbb Z$. En particulier, si $K=\mathbb Q,\mathbb R$ ou $\mathbb C$ l’étude de ces propriétés nous livre des renseignements précieux sur les fonctions polynomiales définies par les éléments de $K[X]$.

1.1.Les polynômes irréductibles

La notion essentielle qui permet de traduire l’arithmétique des polynômes dans la théorie des fonctions est celle de polynôme irréductible, analogue polynomial des nombres premiers.

Définition 1
Un polynôme $P\in K[X]$ est dit irréductible, si ses seuls diviseurs sont les éléments non nuls $a$ de $K$ et les produits de $P$ par de tels éléments.

Autrement dit, les éléments irréductibles de $K[X]$ sont précisément ceux qu’on ne peut pas décomposer de manière « non triviale » en produits de deux polynômes, c’est-à-dire ici en polynômes non constants (où l’indéterminée $X$ apparaît avec une puissance $>0$).

Exemple 1
i) Le polynôme $P=3X^2-4X+5$ est irréductible comme élément de $\mathbb R[X]$, puisque son discriminant $\Delta=(-4)^2-4.3.5=-44$ est strictement négatif. Il est donc a fortiori irréductible comme polynôme de $\mathbb Q[X]$, sinon une décomposition de la forme $P=Q.R$ dans $\mathbb Q[X]$ donnerait une décomposition dans $\mathbb R[X]$. En revanche, il n’est pas irréductible dans $\mathbb C[X]$, puisque l’on a $3X^2-4X+5=3(X-2/3-i\sqrt{11}/3)(X-2/3+i\sqrt{11}/3)$.
ii) Le polynôme $P=X^3-4X+3$ n’est pas irréductible dans $\mathbb R[X]$, car la fonction polynomiale associée $f(x)=x^3-4x+3$ est telle que $\lim\limits_{x\to-\infty} f(x)=-\infty$ et $\lim\limits_{x\to +\infty}f(x)=+\infty$, donc par le théorème des valeurs intermédiaires il existe $a\in \mathbb R$ tel que $f(a)=0$, d’où $X-a$ divise $P$. En revanche, le discriminant de $P$ étant $-4(-4)^3-27.3^2=13>0$, la théorie des équations cubiques nous dit que $P$ possède trois racines complexes, dont une seule ($a$) est réelle. Une division euclidienne de $P$ par $X-a$ fournit la décomposition $X^3-4X+9=(X-a)(X^2+aX+(a^2-4))$, si bien que $X^2+aX+a^2-4$ est un facteur irréductible de $P$ dans $\mathbb R[X]$, et $P$ est donc irréductible dans $\mathbb Q[X]$ si et seulement si $a\notin \mathbb Q$.

1.2.La décomposition en facteurs irréductibles

Rappelons que le Théorème Fondamental de l’Arithmétique énonce que tout entier relatif non nul $n$ se décompose de manière unique sous la forme $n=(\pm 1)\times p_1^{a_1}\times\ldots\times p_r^{a_r}$ avec $r\in\mathbb N$ ($r=0$ si $n=\pm 1$), $p_1<\ldots<p_r$ des nombres premiers distincts et $a_1,\ldots,a_r$ des entiers naturels non nuls. Il s’agit de la célèbre « décomposition en nombres premiers », ceux-ci étant ici considérés comme des entiers naturels, c’est-à-dire des entiers $>0$. Les éléments irréductibles de l’anneau $\mathbb Z$ étant les nombres $\pm p$ pour $p$ un entier naturel premier, et les éléments inversibles de $\mathbb Z$ étant $1$ et $-1$, cette décomposition se reformule comme suit : $n=q_1^{a_1}\times\ldots\times q_r^{a_r}$ avec $p_i=|q_i|$ pour tout $i=1,\ldots,r$. Autrement dit, il s’agit d’une décomposition en éléments irréductibles, « unique » aux éléments inversibles près. Un théorème analogue est valable pour les polynômes de $K[X]$ pour n’importe quel corps $K$, et s’énonce sous la forme suivante :

Théorème 1
Si $P\in K[X]$ est un polynôme non nul, alors il existe une décomposition de $P$ sous la forme $P=Q_1^{a_1}\times\ldots\times Q_r^{a_r}$, avec $r\in \mathbb N$, $Q_1,\ldots,Q_r\in K[X]$ des polynômes irréductibles deux-à-deux non associés et $a_1,\ldots,a_r>0$.

Que les polynômes $Q_i$ soient « deux-à-deux non associés » signifie que deux d’entre eux ne sont pas égaux à une unité près (c’est-à-dire ici un élément non nul de $K$). La décomposition du théorème est alors unique à ces unités près, au sens où si $P=R_1^{b_1}\times\ldots\times R_s^{b_s}$ est une autre décomposition de cette forme, alors $r=s$ (le nombre de facteurs irréductibles non associés est le même), et chaque $Q_i$ est associé à un unique $R_j$ avec $a_i=b_j$, de sorte que $Q_i=u_jR_j$ avec $u_j\in K$ non nul.

Exemple 2
o) En général, un polynôme de degré $1$ est de la forme $aX+b$ avec $a,b\in K$, donc toujours irréductible. Un polynôme de degré $2$ est de la forme $aX^2+bX+c$, et il est irréductible si et seulement si il ne possède pas de racine dans $K$.
i) Dans l’exemple 1(ii), le polynôme $P=X^3-4X+9=(X-a)(X^2+aX+(a^2-4))$ est décomposé en produit de facteurs irréductibles dans $\mathbb R[X]$, puisque les polynômes de la forme $bX+c$ sont toujours irréductibles (o) et que $a$ est la seule racine réelle de $P$ (et donc $X^2+aX+(a^2-4))$ est irréductible).
ii) Le polynôme $P=X^2-2X+2$ est irréductible dans $\mathbb R[X]$ parce que son discriminant est $<0$, et ses racines complexes sont $1+i$ et $1-i$. On a donc une décomposition sous la forme $P=(X-1-i)(X-1+i)$ en deux facteurs irréductibles (linéaires) dans $\mathbb C[X]$. Une autre décomposition est donnée par $P=((1-i)X-2)((1+i)X/2-1)$ : il s’agit essentiellement de la même décomposition, puisque $(1+i)(1-i)=2$.
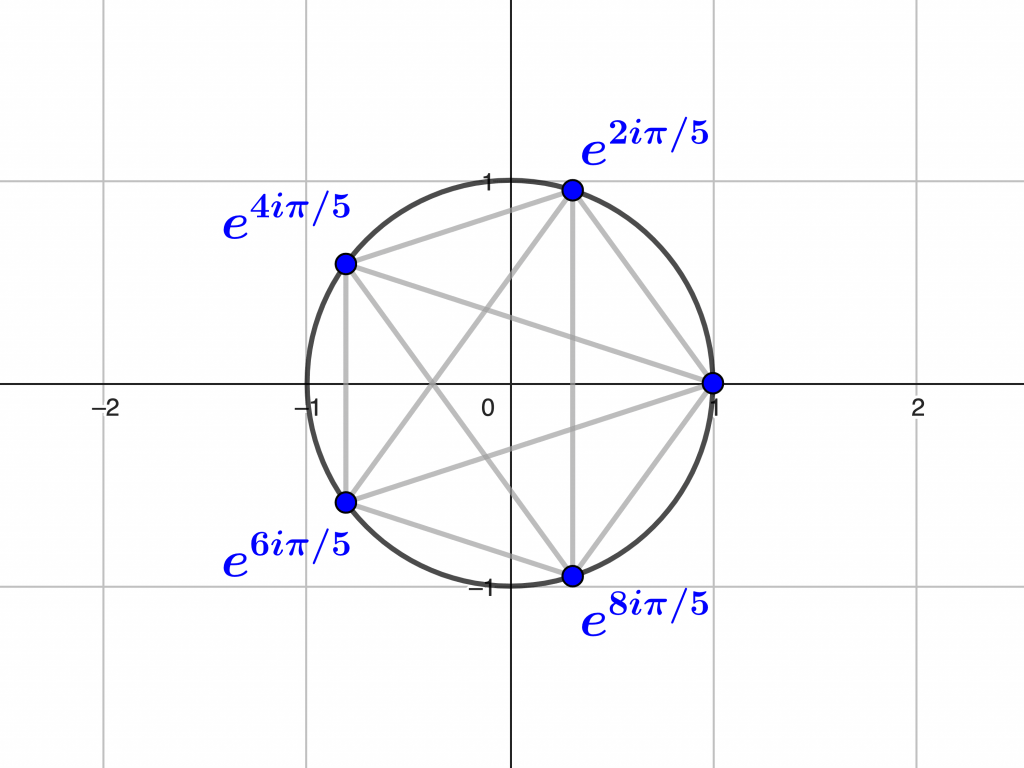
iii) Soit $z=\exp(2i\pi/5)=\cos 2\pi/5+i\sin 2\pi/5$ : on a $z\notin \mathbb R$ et $z+\overline z=2\cos 2\pi/5$, et de plus $z^2\neq z,\overline z$, avec $z^2+\overline z^2=2\cos (4\pi/5)$. Les nombres $1,z,\overline z,z^2,\overline z^2$ sont donc toutes les racines complexes du polynômes $X^5-1$, dont la décomposition en facteurs irréductibles complexes est alors $X^5-1=(X-1)(X-z)(X-\overline z)(X-z^2)(X-\overline z^2)$. On en tire une décomposition en facteurs irréductibles réels de la forme $X^5-1=(X-1)(X^2-2\cos (2\pi/5)X+1)(X^2-2\cos(4\pi/5)+1)$, et en divisant par $X-1$ une factorisation dans $\mathbb Q[X]$ de $X^4+X^3+X^2+X+1$ sous la forme $(X^2-2\cos (2\pi/5)X+1)(X^2-2\cos(4\pi/5)+1)$, irréductible puisque $\cos(2\pi/5)$ et $\cos(4\pi/5)$ sont irrationnels.

En fait, comme pour les nombres premiers dans le cas des entiers relatifs, on peut toujours choisir des facteurs irréductibles « standard », en ne retenant que les polynômes unitaires, c’est-à-dire dont le coefficient de plus haut degré vaut $1$. Un tel polynôme est de la forme $X^n+a_1X^{n-1}+\ldots+a_{n-2}X^2+a_{n-1}X+a_n$ (écriture standard). Alors, la décomposition d’un polynôme non nul $P$ sous la forme $P=u\times Q_1^{a_1}\times\ldots\times Q_r^{a_r}$ avec $Q_1,\ldots,Q_r$ irréductibles et unitaires, et $u\in K$ inversible, est unique.

Exemple 3
Le polynôme $P=5X^6 – 9X^5 – 12X^4 + 53X^3 – 59X^2 + 16X + 6$ se décompose sous la forme $P=(5X+1)(X^2-2X+2)(X^3-4X+3)$ dans $\mathbb Q[X]$, où les exemples 1 et 2 montrent que ces facteurs sont irréductibles. Les facteurs irréductibles unitaires de $P$ sont donc $X+1/5,X^2-2X+2$ et $X^3-4X+3$, et l’unité de la décomposition standard est $5$.

2.Les polynômes irréductibles à coefficients réels

La décomposition en facteurs irréductibles dans $K[X]$ est valable pour n’importe quel « corps de base » $K$. Cependant, nous avons constaté qu’un même polynôme pouvait se décomposer de manière différente selon le corps où l’on considère ses coefficients. Ainsi, en général la forme des facteurs irréductibles peut varier, et c’est pourquoi nous l’étudions en général en fonction du corps de base. Les deux situations les mieux connues sont celles où $K=\mathbb R$ et $K=\mathbb C$, grâce notamment aux outils de l’analyse réelle, et c’est pourquoi nous nous concentrons désormais sur la décomposition irréductible des polynômes de $\mathbb R[X]$ et de $\mathbb C[X]$, en faisant un détour par le cas très différent de $\mathbb Q[X]$.

2.1.Polynômes irréductibles à coefficients rationnels : l’exemple des polynômes cyclotomiques

Les polynômes irréductibles à coefficients dans $\mathbb Q$ peuvent être de degré arbitrairement grand, ce qu’on peut observer sur l’exemple fondamental des polynômes dits « cyclotomiques » (liés au découpage du cercle trigonométrique).

Définition 2
On appelle $n$-ième polynôme cyclotomique (usuel) le polynôme unitaire $\Phi_n(X)=\prod_k (X-e^{2ik\pi/n})$, où $k$ parcourt les entiers de $1$ à $n-1$ qui sont premiers à $n$.

Dans cette écriture, le symbole $\prod_k$ dénote un produit fini, indexé par la variable $k$, et les nombres complexes $e^{2ik\pi/n}=\cos 2k\pi/n+i\sin 2k\pi/n$ sont alors les « racines primitives $n$-ièmes de l’unité », c’est-à-dire les multiples « primitifs » du point $e^{2i\pi/n}$ du cercle trigonométrique, qui le découpe en $n$ parties de longueurs égales. Certaines propriétés permettent de calculer simplement ces polynômes, et les premières valeurs de $n$ donnent :
$\Phi_1(X)=X-1$
$\Phi_2(X)=X+1$
$\Phi_3(X)=X^2+X+1$
$\Phi_4(X)=X^2+1$
$\Phi_5(X)=X^4+X^3+X^2+X+1$ (voir l’exemple 2(iii))
$\Phi_6(X)=X^2-X+1$.

On démontre alors le théorème suivant :

Théorème 2
Chaque polynôme cyclotomique usuel $\Phi_n$ est de degré $\phi(n)$ et irréductible dans $\mathbb Q[X]$.

Rappelons que pour tout entier naturel $n>1$, l’entier $\phi(n)$ est l’indicatrice d’Euler (voir Nombres premiers entre eux et inversion modulaire), soit le nombre d’entiers naturels compris entre $1$ et $n-1$ qui sont premiers à $n$, avec la convention supplémentaire que $\phi(1)=1$. Or, pour tout nombre premier $p$, on a $\phi(p)=p-1$ puisque par définition, $1,2,\ldots,p-1$ sont tous premiers à $p$. Ainsi, le polynôme $\Phi_p$ est de degré $p-1$, et puisqu’il existe une infinité de nombres premiers, il existe des polynômes irréductibles dans $\mathbb Q[X]$ de degré arbitrairement grand.

2.2.Facteurs linéaires des polynômes de $\mathbb R[X]$

A cause de la complétude de l’ensemble des nombres réels, une telle situation ne peut exister pour les polynômes de $\mathbb R[X]$. En effet, tout polynôme non constant $P=a_0+a_1X+\ldots+a_{n-1}X^{n-1}+a_nX^n$ à coefficients réels induit une fonction polynomiale $f(x)=a_0+a_1x+\ldots+a_{n-1}x^{n-1}+a_nx^n$, qui est continue. On peut alors lui appliquer la version suivante du théorème des valeurs intermédiaires :

Théorème 3
Si $f:\mathbb R\to \mathbb R$ est une fonction continue telle que $\lim\limits_{-\infty}=a$ et $\lim\limits_{+\infty}=b$, alors pour tout $c$ compris entre $a$ et $b$ il existe $x$ tel que $f(x)=c$.

Ici, $a$ et $b$ peuvent être l’un des symboles $-\infty$ ou $+\infty$, et l’étude des limites de $f(x)$ en $-\infty$ et $+\infty$ se ramène à l’observation de la parité de $n$ et du signe du coefficient dominant $a_n$. Ainsi, si $n$ est impair, pour $a_n>0$ (resp. $a_n<0$) on a $\lim\limits_{-\infty} f(x)=-\infty$ (resp. $+\infty$) et $\lim\limits_{+\infty} f(x)=+\infty$ (resp. $-\infty$). On en tire la conséquence suivante :

Proposition 1
Tout polynôme $P$ à coefficients réels et de degré impair possède une racine réelle.

En particulier, les polynômes à coefficients rationnels et de degré impair ont donc toujours au moins une racine réelle, ce à quoi l’incomplétude de l’ensemble $\mathbb Q$ fait obstacle dans $\mathbb Q$. En général, si $P$ est un polynôme à coefficient réels de degré impair $n=2k+1$, il possède une racine réelle $a$, et on peut le factoriser sour la forme $P=(X-a).Q$, où $Q$ est de degré pair $2k$ : les polynômes irréductibles à coefficients réels sont donc forcément soit linéaires (de la forme $aX+b$), soit de degré pair !

2.3.Les polynômes irréductibles de degré $2$

L’étude des polynômes irréductibles de $\mathbb R[X]$ ne s’achèvera pourtant qu’avec la détermination des polynômes irréductibles de $\mathbb C[X]$ grâce au « théorème fondamental de l’algèbre » (théorème 5) : nous aurons alors besoin de caractériser les polynômes à coefficients réels de degré $2$ qui sont irréductibles. Rappelons la définition suivante :

Définition 3
Si $P=aX^2+bX+c$ est un polynôme quadratique (de degré $2$, avec donc $a\neq 0$) à coefficients réels, le discriminant de $P$ est le nombre réel $\Delta=b^2-4ac$.

Le polynôme $P$ étant de degré $2$, il est irréductible si et seulement si il ne possède pas de racine réelle, et on peut alors utiliser le discriminant pour le réécrire sous une forme qui permet d’en étudier immédiatement les racines. Il s’agit de faire apparaître une différence de carrés en utilisant l’identité remarquable $A^2+B^2=(A+B)^2-2AB$ : en factorisant par $a\neq 0$, on a en effet $$P=a.[X^2+(b/a)X+c/a]=a[(X+b/2a)^2-(b^2-4ac)/4a^2].$$ A partir de l’identité $A^2-B^2=(A+B).(A-B)$, on remarque alors que :

1. Si $\Delta=b^2-4ac\geq 0$, c’est le carré d’un nombre réel $d$, de sorte que $P=a[(X+b/2a)-d/2a][(X+b/2a)+d/2a]$, si bien que $P$ possède deux racines réelles, $X_1=\dfrac{-b+\sqrt\Delta}{2a}$ et $X_2=\dfrac{-b-\sqrt\Delta}{2a}$, éventuellement égales si $\Delta=0$ : dans ce cas, $P$ n’est pas irréductible
2. SI $\Delta<0$, alors pour tout nombre réel $x$ on a $|P(x)|=|a|.[(x+b/2a)^2-\Delta/4a^2]>0$, puisque l’expression entre crochets dénote un nombre $>0$ : dans ce cas, $P$ n’a aucune racine réelle, il est donc irréductible.

Nous avons ainsi démontré :

Théorème 4
Les polynômes quadratiques irréductibles à coefficients réels sont ceux dont le discriminant est $<0$.

3.Les polynômes irréductibles à coefficients complexes

3.1.Le théorème fondamental de l’algèbre

Les grands domaines des mathématiques sont souvent affublés d’un « théorème fondamental » (arithmétique, analyse, algèbre…), lequel énonce une propriété essentielle de leurs concepts fondateurs, et qui est utilisée de manière ubiquitaire. L’algèbre étant née de la théorie des nombres (en fait, de la théorie des équations), son théorème fondamental a trait à la situation naturelle où toutes les équations possèdent une solution, advenue avec l’invention des nombres complexes. En termes de polynômes, ce théorème se formule donc de la manière suivante :

Théorème 5 (de d’Alembert-Gauss)
Tout polynôme non constant et à coefficients complexes possède une racine dans $\mathbb C$.

En particulier, les polynômes non constants à coefficients réels ont donc toujours au moins une racine complexe, ce à quoi l’ordre sur l’ensemble $\mathbb R$ faisait obstacle dans $\mathbb R$, puisque les réels strictement négatifs ne peuvent y avoir de racine carrée. Ce théorème remarquable est évidemment faux sur tous les autres corps naturels de nombres que nous évoquons souvent, c’est-à-dire ici $\mathbb Q$ et $\mathbb R$ (et les corps finis $\mathbb F_q$) : nous avons vu que les polynômes cyclotomiques sont irréductibles dans $\mathbb Q[X]$, et que les polynômes quadratiques réels de discriminant $<0$ (par exemple $X^2+X+1$) sont irréductibles dans $\mathbb R[X]$. Il existe pourtant toute une famille de corps, dits « algébriquement clos », dans lesquels ce théorème est vrai, et à partir desquels on développer la théorie des nombres et la géométrie algébrique…

Exemple 4
Pour tout entier naturel $n\geq 1$, le polynôme cyclotomique $\Phi_n$ possède par définition toutes ses racines dans $\mathbb C$, qui sont toutes des points du cercle trigonométrique. Par exemple, $\Phi_2=X^2+1$ a pour racines $i$ et $-i$, et $\Phi_3=X^2+X+1$ a pour racines $j$ et $j^2=\overline j$, avec $j=e^{2i\pi/3}=-1/2+i\sqrt 3/2$.

Ceci étant dit, la démonstration du théorème fondamental de l’algèbre – que nous laissons ici de côté – repose essentiellement sur les propriétés de l’ensemble $\mathbb R$, et notamment la proposition 1, qui énonce une propriété analogue pour les polynômes à coefficients réels, avec toutefois une condition sur le degré.

3.2.Polynômes irréductibles à coefficients complexes