La définition d’un cercle est simple : il s’agit d’un ensemble de points situés à une même distance d’un point donné. Cette distance est appelée le rayon et ce point le centre du cercle.
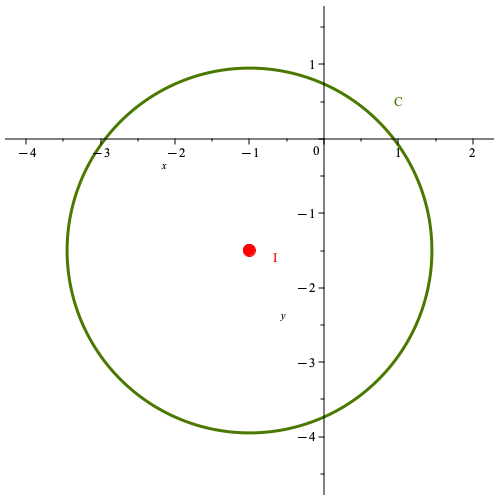
Figure réalise avec Maple
1. Les cercles comme ensembles de solutions d’une équation
Mais qu’est-ce qu’un point, et qu’est-ce qu’une distance ? Si nous en avons une intuition tout-à-fait claire, celle-ci ne suffit pas pour parler de manière rigoureuse de ces choses en mathématique.
1.1. La distance euclidienne
Nous avons évoqué dans l’article Le Plan euclidien : géométrique antique et approche analytique comment il est possible de donner un sens précis à la notion de point et à la notion de distance dans le cadre du plan euclidien moderne \(\mathbb R^2\) : grâce à la construction moderne des nombres réels, tout nombre réel positif possède une racine carrée, et deux points \(M\) et \(N\) étant représentés par leurs coordonnées respectives \((x,y)\) et \((t,u)\) dans l’approche cartésienne de la géométrie, la distance \(d(M,N)\) entre ces deux points est la racine carrée de la somme des carrés des distances entre leurs coordonnées, soit \(d(M,N)=\sqrt{(x-t)^2+(y-u)^2}\), ce qui est une reformulation du théorème de Pythagore.
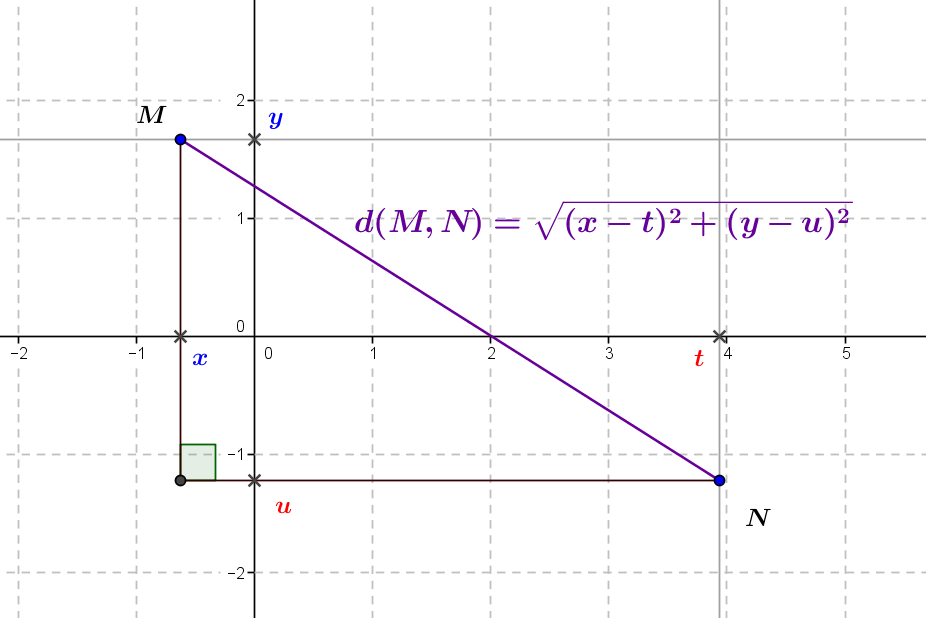
1.2. Définition analytique d’un cercle du plan
De ce point de vue, nous avons une description « analytique » parfaitement claire de ce qu’est un cercle dans le plan, à partir de la définition du départ : le cercle \(\mathscr C\) de centre \(I=(a,b)\) et de rayon \(R\) (nombre réel positif) est l’ensemble des points \(M=(x,y)\) du plan \(\mathbb R^2\) tels que la distance \(d(I,M)\) entre \(I\) et \(M\) vaut \(R\), soit, puisque la distance \(d(I,M)\) vaut \(\sqrt{(x-a)^2+(y-b)^2} \), symboliquement \[\mathscr C=\{(x,y)\in\mathbb R^2 | \sqrt{(x-a)^2+(y-b)^2}=R\}.\] Comme le nombre \(R\) est positif, on peut alors se passer de la racine carrée pour décrire finalement le cercle \(\mathscr C\) comme l’ensemble \[\mathscr C=\{(x,y)\in \mathbb R^2 | (x-a)^2+(y-b)^2=R^2\},\] ce qui nous donne l’équation typique d’un cercle dans le plan, ici \((x-a)^2+(y-b)^2=R^2\) pour le cercle \(\mathscr C\) de centre \(I=(a,b)\) et de rayon \(R\).
Autrement dit, un tel cercle est l’ensemble des solutions \((x,y)\) de cette équation : grâce à la méthode analytique de Descartes, on peut décrire un cercle dans le plan comme un ensemble de solutions d’une équation, de manière analogue à la description d’une droite comme ensemble de solutions d’une équation. Par exemple, le cercle du début a pour équation \((x+1)^2+(y+\frac 3 2)^2=6\).
2. Le cercle trigonométrique : le cosinus et le sinus comme coordonnées angulaires
2.1. Repérer un point du cercle trigonométrique
Or, on dispose au moyen de l’analyse réelle (théorie des fonctions de l’ensemble \(\mathbb R\)) de deux fonctions, le cosinus et le sinus, dites « trigonométriques », et qui nous donnent les coordonnées d’un point du cercle trigonométrique, qui est le cercle de centre \(O=(0,0)\) et de rayon \(1\). En effet, un point \(M=(x,y)\) sur ce cercle est repéré par l’angle qu’il décrit avec l’axe \([0x)\), qu’on mesure comme la longueur (orientée) de l’arc de cercle délimité par le point \(I=(0,1)\) et le point \(M\), ce qu’on appelle la mesure en radians de l’angle \(\widehat{IOM}\). Autrement dit, si la longueur de l’arc \(\overset{\frown}{IM}\) est \(t\), les coordonnées (cartésiennes) du point \(M\) sont \(x=\cos t\) et \(y=\sin t\) : le cosinus et le sinus de l’angle \(t\) sont les projections du point \(M\) sur chaque axe.
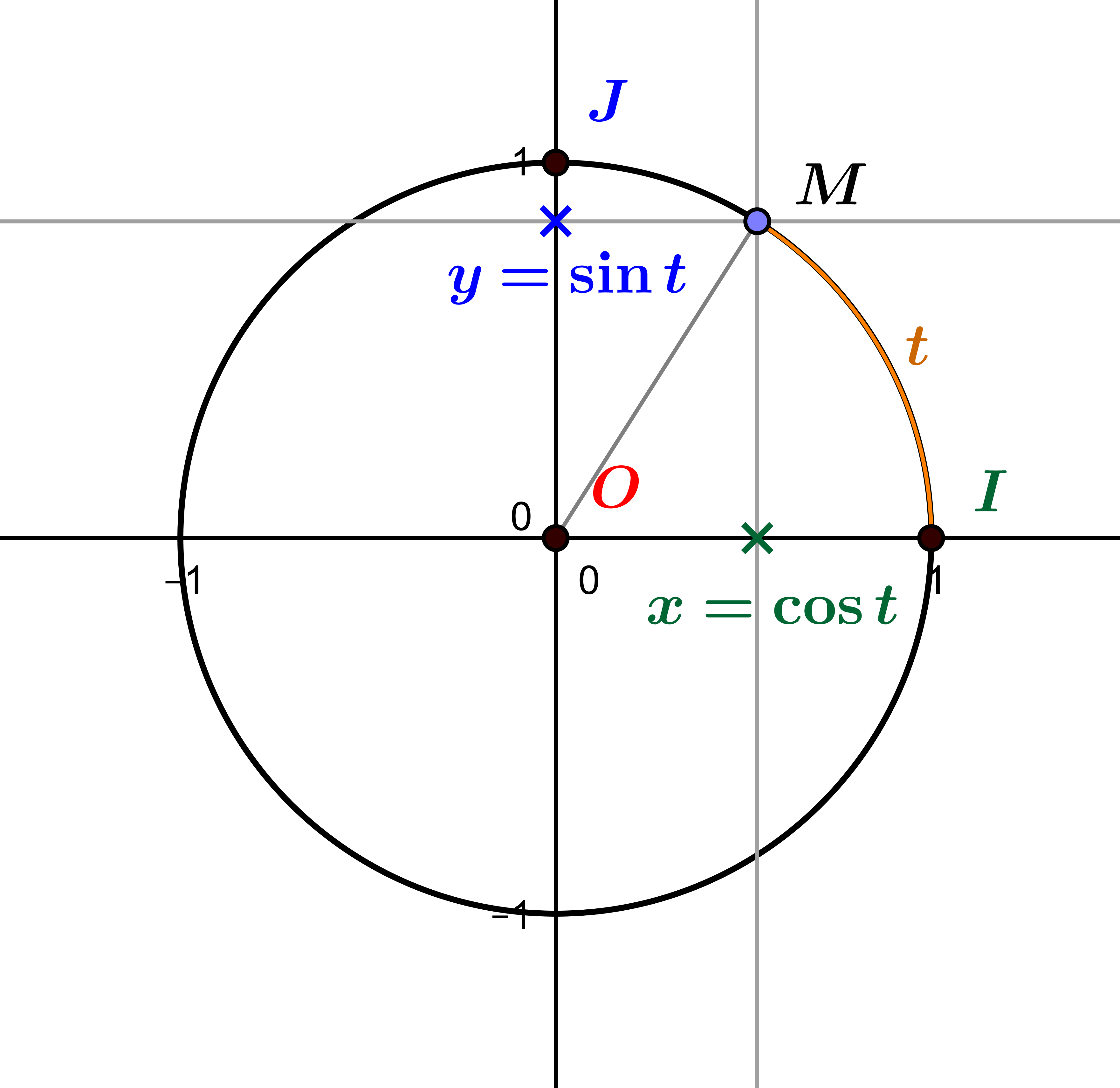
Le cercle trigonométrique et les coordonnées d’un point \(M\) sur ce cercle, exprimées comme cosinus et sinus de l’angle \(\widehat{IOM}\) de mesure \(t\) radians
2.2. Le cercle unité comme image d’une fonction
Bienvenue sur La Règle et le Compas ! Pour lire les articles du blog en intégralité, merci de vous connecter. Si ce n'est déjà fait, vous pouvez vous inscrire librement ici sur MATHESIS.
Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :
Pour aller plus loin
Commencer en mathématiques : Mathesis I.1 – Entrer dans l’Univers Mathématique

0 commentaires