Le paradoxe ou antinomie de Russell est un paradoxe très simple de la théorie naïve des ensembles, qui surgit lorsqu’on cherche à définir un « ensemble de tous les ensembles ». Sa résolution repose sur l’introduction de la notion de classe et la distinction des ensembles parmi les classes. Grâce à la théorie des classes, il est alors possible de transfigurer la théorie naïve des ensembles grâce à la théorie des ordinaux et des cardinaux.

1.Le paradoxe ou antinomie de Russell

1.1.L’ensemble de tous les ensembles

Le paradoxe de Russell, du nom du philosophe, mathématicien et logicien britannique Bertrand Russell, montre les limites logiques d’une utilisation trop large du concept d’ensemble en théorie naïve des ensembles. Ce paradoxe apparaît lorsque nous considérons la possibilité d’un « ensemble de tous les ensembles« .

Tout part de la simple constatation suivante : si un tel ensemble \(E\) existe, c’est-à-dire est permis dans la théorie, alors il est nécessairement, en tant qu’ensemble, un élément de lui-même.

Bertrand Russell, philosophe, mathématicien et logicien britannique

1.2.Le sous-ensemble des ensembles qui n’appartiennent pas à eux-mêmes

Cette propriété est assez contre-intuitive : on distingue en général un ensemble des éléments qu’il contient, la théorie des ensembles est en quelque sorte faite pour cela. Cependant, elle n’apparaît pas contradictoire comme telle. Mais parmi les ensembles, nous pourrions considérer seulement ceux qui ne sont pas éléments d’eux-mêmes.

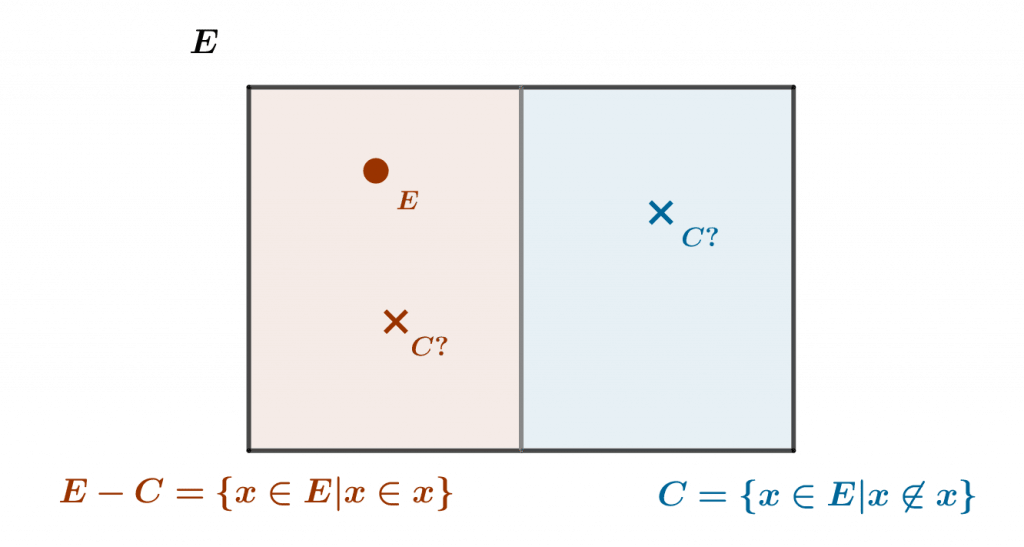
Cette propriété est tout-à-fait univoque en théorie naïve des ensembles, et permet donc, puisqu’on a supposé l’existence de \(E\), de définir le sous-ensemble \(C\) de \(E\) formé de tous les ensembles qui ne s’appartiennent pas eux-mêmes, symboliquement \(C=\{x\in E : x\notin x\}\).

1.3.La formulation du paradoxe

On pose alors la question suivante : l’ensemble \(C\) est-il élément de lui-même ? Etant donné que la logique mathématique naturelle est ici considérée comme « classique », le principe du tiers exclu est valide : soit cet énoncé est vrai, soit sa négation est vraie. Supposons d’abord que \(C\) est élément de lui-même, autrement dit que \(C\in C\) : comme \(C\in E\), par définition de \(C\) on en déduit que \(C\notin C\), ce qui contredit l’hypothèse.

Supposons alors que \(C\notin C\) : on doit en déduire, par définition de \(C\), que \(C\in C\), ce qui contredit à nouveau l’hypothèse ! Ainsi, aucune des deux alternatives imposées par le principe du tiers exclu, à savoir que \(C\in C\) ou \(C\notin C\), ne peut être vraie, ce qui contredit la logique mathématique naturelle. C’est une version de ce qu’on appelle le paradoxe de Russell.

2.Résoudre le paradoxe par la théorie des classes

2.1.Distinguer les ensembles parmi les classes

Retrouvez cet article en vidéo sur MATHESIS, la chaîne YouTube :