La représentation du plan euclidien par le produit cartésien \(\mathbb R^2\) permet de décomposer tout vecteur du plan en deux coordonnées, son abscisse et son ordonnée. Cette décomposition est liée à un « système de représentation » particulier et naturel, qu’on appelle une base. Il existe une infinité de telles bases, et parmi elles une infinité de bases dites orthonormées.

1.La base canonique et les bases du plan euclidien

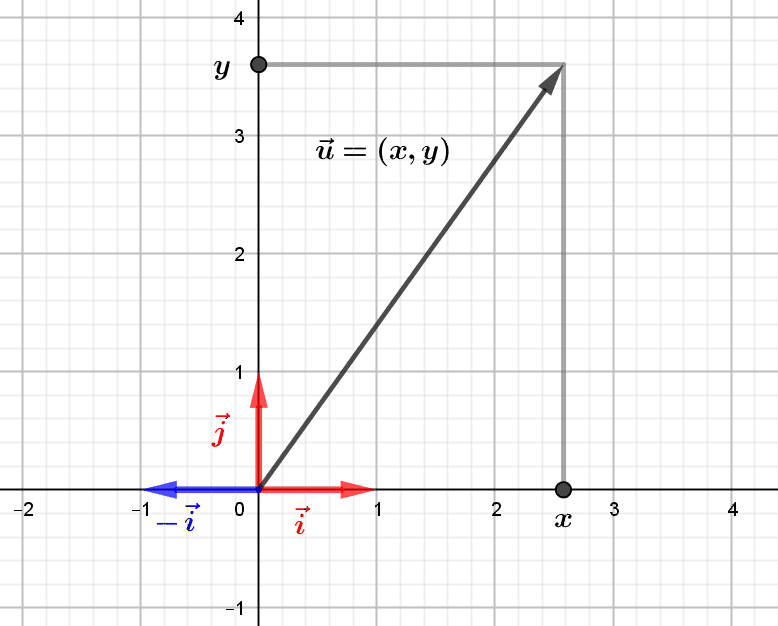
1.1.La représentation naturelle d’un vecteur dans la base canonique

Tout vecteur \((x,y)\) du plan euclidien se représente sous la forme \((x,y)=x.(1,0)+y.(0,1)\), et ceci de manière unique : si \((x,y)=u.(1,0)+v.(0,1)\), alors \((x,y)=(u,0)+(0,v)=(u,v)\), donc \(x=u\) et \(y=v\). On dit que les vecteurs \(\vec i=(1,0)\) et \(\vec j=(0,1)\) forment la base canonique \((\vec i,\vec j)\) du plan euclidien \(\mathbb R^2\). Les nombres réels \(x\) et \(y\), abscisse et ordonnée du vecteur \(\vec u=(x,y)\), sont les coordonnées du vecteur \(\vec u\) dans cette base canonique. Toutefois, bien que cette manière de décomposer un vecteur dans la base canonique soit complètement naturelle, il est possible d’effectuer une telle décomposition dans multitude d’autres « systèmes de représentations », appelés bases, du plan euclidien.

1.2.Problème : décrire les autres bases du plan euclidien

Il est souvent utile, en effet, de pouvoir changer de système de représentation, par exemple lorsqu’on décrit un mouvement par une courbe. Dans ce cas, on choisit un système de représentation associé au point mobile décrit par la courbe, et possédant des propriétés géométriques intéressantes. Dans cet article nous voulons décrire proprement ce que sont les bases du plan, et introduire de manière rigoureuse la notion fondamentale de base orthonormée.

2.Décrire les bases du plan par un critère analytique simple

2.1.La direction d’un vecteur non nul

On peut comprendre la notion de base dans le plan de manière simple, à partir de celle de direction d’un vecteur non nul. Si \(\vec u=(a,b)\) est un vecteur non nul, il détermine en effet une droite vectorielle, qui est l’ensemble des vecteurs \(\vec v=(x,y)\) qui sont proportionnels à \(\vec u\), autrement dit qui sont de la forme \(\vec v=\lambda.\vec u\), soit \((x,y)=(\lambda.a,\lambda.b)\). Cette droite est la direction du vecteur \(\vec u\), et on peut facilement montrer qu’un vecteur quelconque \(\vec v=(x,y)\) est sur cette droite si et seulement si l’équation \[(*)\ -bx+ay=0\] est vérifiée.

2.2.Couples de vecteurs non nuls et colinéaires

Ceci étant établi, on dit que deux vecteurs non nuls \(\vec u=(a,b)\) et \(\vec v=(c,d)\) sont colinéaires (c’est-à-dire parallèles) si ils ont la même direction, c’est-à-dire déterminent la même droite \(D\). Cela revient exactement à dire que \(\vec v\) est sur la direction de \(\vec u\), autrement dit que l’équation \(-bc+ad=0\) est vérifiée, grâce à la condition \((*)\). Le nombre réel $ad-bc$, qui apparaît partout en géométrie plane, est appelé déterminant des vecteurs $u$ et $v$. Or, dans un tel cas toute combinaison linéaire de \(\vec u\) et \(\vec v\), c’est-à-dire tout vecteur de la forme \(\vec w=\alpha.\vec u+\beta.\vec v,\) avec des coefficients \(\alpha,\beta\in\mathbb R\), est forcément aussi sur la droite \(D\). En effet, on peut écrire \(\vec w=(\alpha.a,\alpha.b)+(\beta.c,\beta.d)=(\alpha.a+\beta.c,\alpha.b+\beta.d)\), et vérifier par exemple que \(-b.(\alpha.a+\beta.c)+a.(\alpha.b+\beta.d)=0\). Autrement dit, si \(\vec u\) et \(\vec v\) sont colinéaires, il est impossible de « décomposer » d’autres vecteurs que ceux de \(D\) à partir de \(\vec u\) et \(\vec v\) !

2.3.Caractériser les bases du plan par la colinéarité

Ainsi, pour obtenir une « base » du plan, c’est-à-dire un système de représentation en coordonnées pour tous les vecteurs du plan, il faut choisir au moins deux vecteurs non nuls et non colinéaires \(\vec u=(a,b)\) et \(\vec v=(c,d)\). On peut alors démontrer que tout vecteur \(\vec w=(x,y)\) du plan \(\mathbb R^2\) se décompose de manière unique en fonction de \(\vec u\) et \(\vec v\), c’est-à-dire qu’il existe un unique couple de nombres réels \((\alpha,\beta)\) tel que \(\vec w=\alpha.\vec u+\beta.\vec v\). En effet, dire que \(\vec u\) et \(\vec v\) ne sont pas colinéaires, c’est dire maintenant que \(-bc+ad\neq 0\), c’est-à-dire \(ad-bc\neq 0\). On résout alors un système de deux équations à deux inconnues traduisant cette égalité, à savoir \[\left\lbrace\begin{array}{cc} x & = & \alpha.a + \beta.b\\y & = & \alpha.c + \beta.d.\end{array}\right.\] On trouve \(\alpha=\dfrac{1}{ad-bc}.(dx-cy)\) et \(\beta=\dfrac{1}{ad-bc}.(ay-bx)\), et on peut vérifier par le calcul qu’on obtient bien une décomposition de \(\vec w\), dont on peut montrer qu’elle est unique.

3.Bases orthonormées

3.1.Vecteurs orthogonaux et unitaires