Le cercle trigonométrique permet de définir le cosinus, le sinus et la tangente d’un angle orienté, et d’en donner une interprétation à travers les théorèmes de Thalès et de Pythagore.

Introduction : trigonométrie et fonctions

1.Le cercle trigonométrique et la représentation circulaire des angles

1.1.Unités pratiques et angles orientés

Les unités de mesure pratiques des angles sont le degré et le grade; un angle plein (c’est-à-dire un tour complet) mesure 360 degrés ou 400 grades, un angle plat (c’est-à-dire un demi-tour) mesure 180 degrés ou 200 grades, un angle droit (c’est-à-dire un quart de tour) mesure 90 degrés ou 100 grades.

Nous parlerons ici d’angles orientés. Un tel angle est représenté par deux demi-droites basées en un même point, et sa mesure est considérée comme positive dans le sens direct (c’est-à-dire giratoire ou anti-horaire, sens inverse des aiguilles d’une montre). Quitte à effectuer une translation et une rotation, on peut toujours représenter un tel angle à partir de l’origine du plan, en prenant comme première demi-droite le demi-axe des abscisses positives (voir la figure suivante).

Pour parler de la mesure d’un angle orienté, il faut l’affubler d’un signe. Par exemple, un demi-tour à gauche correspond à un angle de 90 degrés tandis qu’un demi-tour à droite correspond à un angle de -90 degrés.

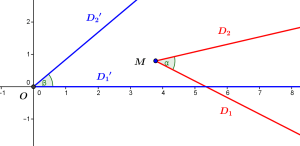
L’angle orienté \(\alpha\) entre les demi-droites \(D_1\) et \(D_2\) est le même que l’angle orienté \(\beta\) entre les demi-droites \(D_1’\) et \(D_2’\), et sa mesure est de 40 degrés. On transporte \(\alpha\) en \(\beta\) par une rotation et une translation, qui déplacent \(M\) en \(O\), \(D_1\) en \(D_1’\), et \(D_2\) en \(D_2’\). La mesure de l’angle orienté entre \(D_2\) et \(D_1\) (ou entre \(D_2’\) et \(D_1’\)) est -40 degrés.

1.2.La mesure des angles en radians

L’unité de mesure mathématique, c’est-à-dire théorique, des angles orientés, est le radian. A quoi correspond cette façon de mesurer les angles, autrement dit à quoi correspond cette unité de mesure ? La mesure des angles en radians, positive ou négative si nous parlons d’angles orientés, est relative à la représentation des angles sur le cercle de centre \((0,0)\) et de rayon \(1\) (voir Tracer un cercle sur le plan : équations et paramètres), qu’on appelle cercle trigonométrique.

Un angle orienté entre deux demi-droites étant rapporté à l’origine du plan euclidien et au demi-axe des abscisses positives, la première demi-droite identifiée avec la partie positive de l’angle des abscisses, on considère l’intersection de la seconde demi-droite avec le cercle trigonométrique. Cette intersection est un point du plan, qui détermine l’extrémité d’un arc de cercle basé au point \((1,0)\) et noté \(I\). Par définition, la mesure de l’angle, en radians, est la longueur de cet arc de cercle, affublée d’un signe selon l’orientation de l’angle (soit selon que l’arc est parcouru dans le sens direct ou le sens indirect).

Ainsi, en admettant que le périmètre du cercle trigonométrique est $2\pi$, la mesure de l’angle plein direct est alors \(2\pi\); celle de l’angle plat direct est \(\pi\) et celle de l’angle droit direct est \(\pi/2\).

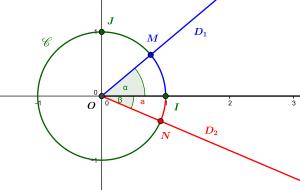
Le cercle \(\mathscr C\) est le cercle trigonométrique, centrée en \(O=(0,0)\) et de rayon \(1\). L’angle orienté \(\alpha\) est représenté par l’axe des abscisses positives (la demi-droite \([OI)\)) et la demi-droite \(D_1\), et sa mesure en radians est donc la longueur de l’arc (orienté) \(\overset{\frown}{IM}\), soit ici \(2\pi/9\). L’angle \(\beta\), orienté dans l’autre sens, est représenté par la demi-droite \([OI)\) et la demi-droite \(D_2\), et sa mesure en radians est donc la longueur de l’arc orienté \(\overset{\frown}{IN}\), affublée d’un signe négatif, soit ici \(-23\pi/180\).

2.Les fonctions trigonométriques des angles

2.1.Les coordonnées circulaires

Ainsi, un angle orienté peut toujours être représenté par un point placé sur le cercle trigonométrique. Or, en considérant les coordonnées de ce point (voir Le Plan euclidien : géométrie antique et approche analytique), c’est-à-dire en projetant ce point sur l’axe des abscisses d’une part, sur l’axe des ordonnées d’autre part, on obtient deux nombres réels, qui sont les coordonnées du point, et que nous appellerons les coordonnées circulaires de l’angle orienté.

La première coordonnée circulaire de l’angle, obtenue comme abscisse du point qu’il détermine sur le cercle trigonométrique, est appelée le cosinus de l’angle. On note \(\cos\alpha\) le cosinus d’un angle orienté \(\alpha\). La seconde coordonnée circulaire de l’angle, obtenue comme ordonnée du point qu’il détermine sur le cercle trigonométrique, est appelée le sinus de l’angle. On note \(\sin\alpha\) le sinus d’un angle orienté \(\alpha\).

Il faut bien noter que le cosinus et le sinus sont définis ici pour un angle orienté et non pour un nombre réel ! Il s’agit donc des coordonnées circulaires d’une grandeur géométrique, et pas du cosinus et du sinus d’un nombre réel, qui sont fondamentalement associés au cosinus et au sinus d’un angle, mais à travers des grandeurs numériques (les mesures de l’angle).

L’angle \(\alpha\) formé par le demi-axe des abscisses positives et la droite \(D_1\) est représenté par le point d’intersection \(M\) de cette droite avec le cercle trigonométrique \(\mathscr C\). Les coordonnées du point \(M\) sont par définition le cosinus de l’angle \(\alpha\) (abscisse \(\cos\alpha\) de \(M\)) et le sinus de l’angle \(\alpha\) (ordonnée \(\sin\alpha\) de \(M\)).

2.2.Fonctions trigonométriques

Retrouvez l’article en vidéo sur Mathesis, la chaîne YouTube :

Pour aller plus loin