Un ensemble fini, c’est un ensemble qu’on peut dénombrer à l’aide des entiers naturels \(1,\ldots,n\) pour un certain entier naturel \(n\). Mais qu’est-ce que dénombrer ? Et qu’est-ce qu’un ensemble infini ?
1. Comparer des ensembles : la notion de bijection
Les notions d’ensemble fini et d’ensemble infini, et la conceptualisation mathématique du « comptage » (des éléments) d’un ensemble, sont intimement liées et permettent de distinguer et définir rigoureusement le fini et l’infini mathématiques, sans autre ressource conceptuelle que la théorie naïve des ensembles (voir Qu’est-ce qu’un ensemble ?).
Pour compter les éléments d’un ensemble (on dit dénombrer), on utilise la notion de bijection. Une bijection entre deux ensembles \(E\) et \(F\) est une fonction (on dit aussi une application) de \(E\) dans \(F\), c’est-à-dire un « procédé » ou une « opération » \(f\) qui transforme les éléments de \(E\) en des éléments de \(F\) (on dit mathématiquement que \(f\) associe à chaque élément \(x\) de \(E\) un élément \(y\), noté \(f(x)\), de \(F\)), de manière très particulière : \(f\) est une bijection précisément lorsque chaque élément de \(F\) est associé par \(f\) à au plus un élément de \(E\) (on parle de fonction injective) et que tout élément de \(F\) est associé à au moins un élément de \(E\) (on parle de fonction surjective).
Autrement dit, une fonction \(f:E\to F\) est une bijection exactement lorsque qu’elle met en correspondance, un à un, les éléments de \(E\) et de \(F\) ! On doit ainsi souvent traduire de manière un peu détournée des idées très simples pour leur donner une certaine rigueur mathématique. Cette façon d’apparier un à un les éléments de deux ensembles est en fait une manière naturelle d’en comparer les quantités, avant même de les compter : les enfants procèdent souvent ainsi !
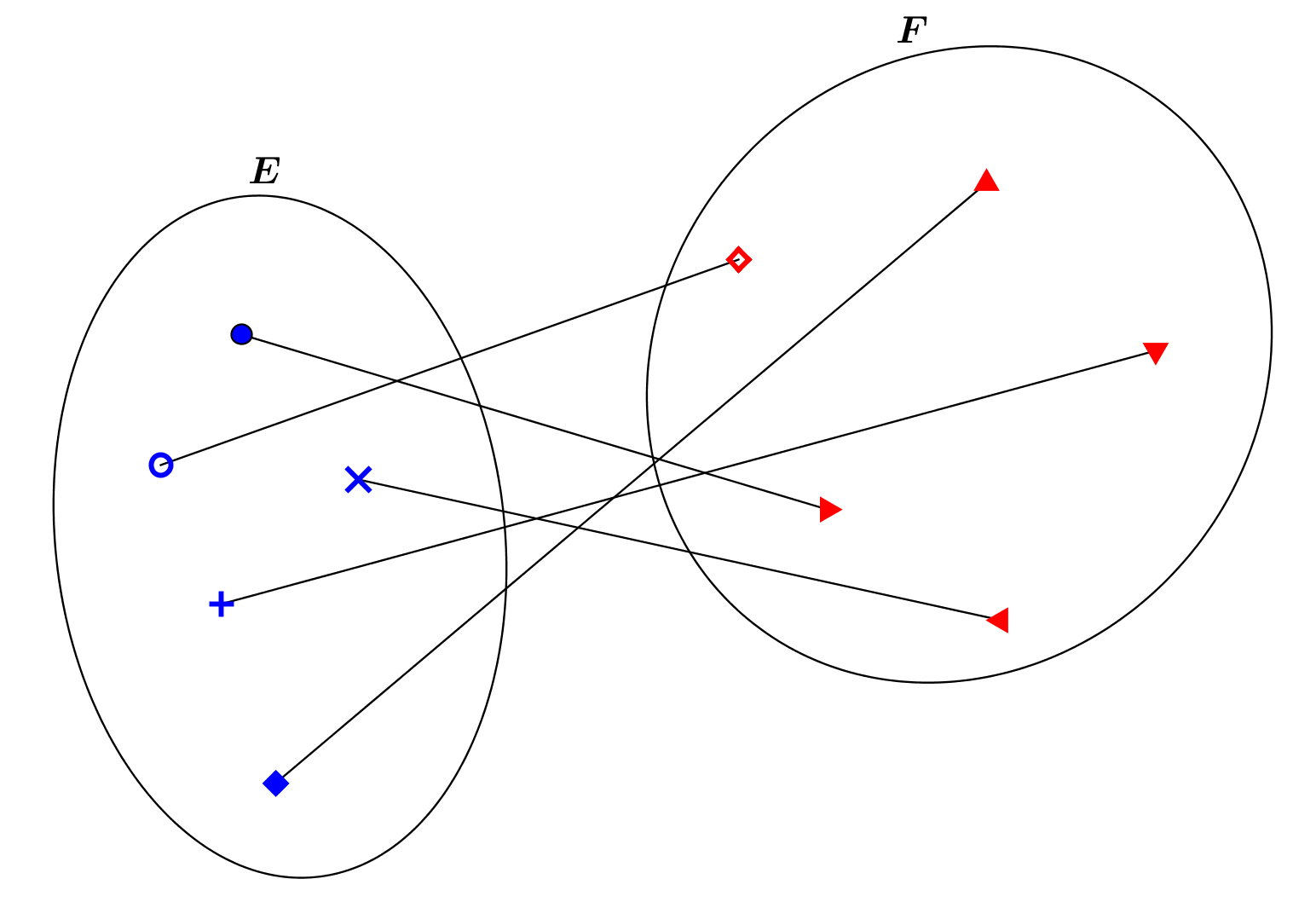
Cette figure illustre l’existence d’une bijection entre les ensembles \(E\) et \(F\) : on a mis en correspondance « un-à-un » les éléments de l’un et de l’autre. Il existe plusieurs manières de le faire, on peut d’ailleurs les dénombrer précisément.
2. Les ensembles finis sont ceux qu’on peut dénombrer
2.1. Définition des ensembles finis
En utilisant cette notion élémentaire mais fondamentale de bijection, on peut définir rigoureusement ce qu’est un ensemble fini. Un ensemble fini, c’est un ensemble dont on peut théoriquement compter les éléments, ce qu’on appelle « dénombrer », autrement dit un ensemble qui est en bijection avec un ensemble de la forme \(\{1,2,3,\ldots,n\}\) (soit tous les nombres entiers de \(1\) à \(n\)) pour un certain entier naturel \(n\) . Cette définition simple conceptualise précisément la façon dont nous comptons : alors qu’on peut comparer deux ensembles en les mettant en bijection, on compte un ensemble en associant à chacun de ses éléments un et un seul nombre entier entre \(1\) et le « nombre d’éléments » de cet ensemble (qui vaut \(0\) si l’ensemble est vide…) ! Mathématiquement, comparer deux ensembles ou dénombrer un ensemble revient donc à la même chose, décrire une bijection; seulement, lorsqu’on dénombre, on décrit une bijection avec un ensemble particulier, un ensemble de nombres.
2.2. Compter des différentes manières
L’ensemble des nombres de \(1\) à \(n\) est noté \([[1,n]]\). A un ensemble fini \(E\), on peut donc attacher un nombre d’éléments, qui est l’entier naturel \(n\) qu’on obtient en mettant, par définition, \(E\) en bijection avec l’ensemble \([[1,n]]\). L’expérience nous montre que quelle que soit la manière dont on compte, on aboutit au même résultat; mais est-ce théoriquement vrai, autrement dit est-il impossible de compter un ensemble fini de deux façons différentes et d’obtenir deux résultats différents ? Même si il paraît étrange de se poser la question, cela ne fait pas partie de la définition, et la rigueur mathématique exige que cela soit démontré ! C’est en effet un théorème, qui demande un peu de réflexion. Et la question est loin d’être anodine, puisque lorsqu’on énumère un ensemble infini, du moins en utilisant ce qu’on appelle un nombre « ordinal », on peut aboutir à des résultats différents…
2.3. Le cardinal d’un ensemble fini
Pour revenir aux ensembles finis, puisque n’importe quelle manière de dénombrer un ensemble \(E\) – c’est-à-dire, conceptuellement, n’importe quelle bijection entre \(E\) et un ensemble de la forme \([[1,n]]\) – donne le même résultat, on peut définir le nombre d’éléments de \(E\) comme cet unique nombre entier naturel \(n\), qu’on appelle aussi le cardinal de \(E\) (et dans le cas où le cardinal d’un ensemble infini peut être défini, il ne dépend pas non plus de la manière de compter). Certaines autres propriétés « évidentes » des ensembles finis demandent à être établies rigoureusement, c’est-à-dire démontrées : par exemple, qu’un sous-ensemble \(S\) d’un ensemble fini \(E\) est lui-même fini, et qu’il possède moins d’éléments que \(E\) ! De même, il faut démontrer que la réunion de deux ensembles finis est un ensemble fini…
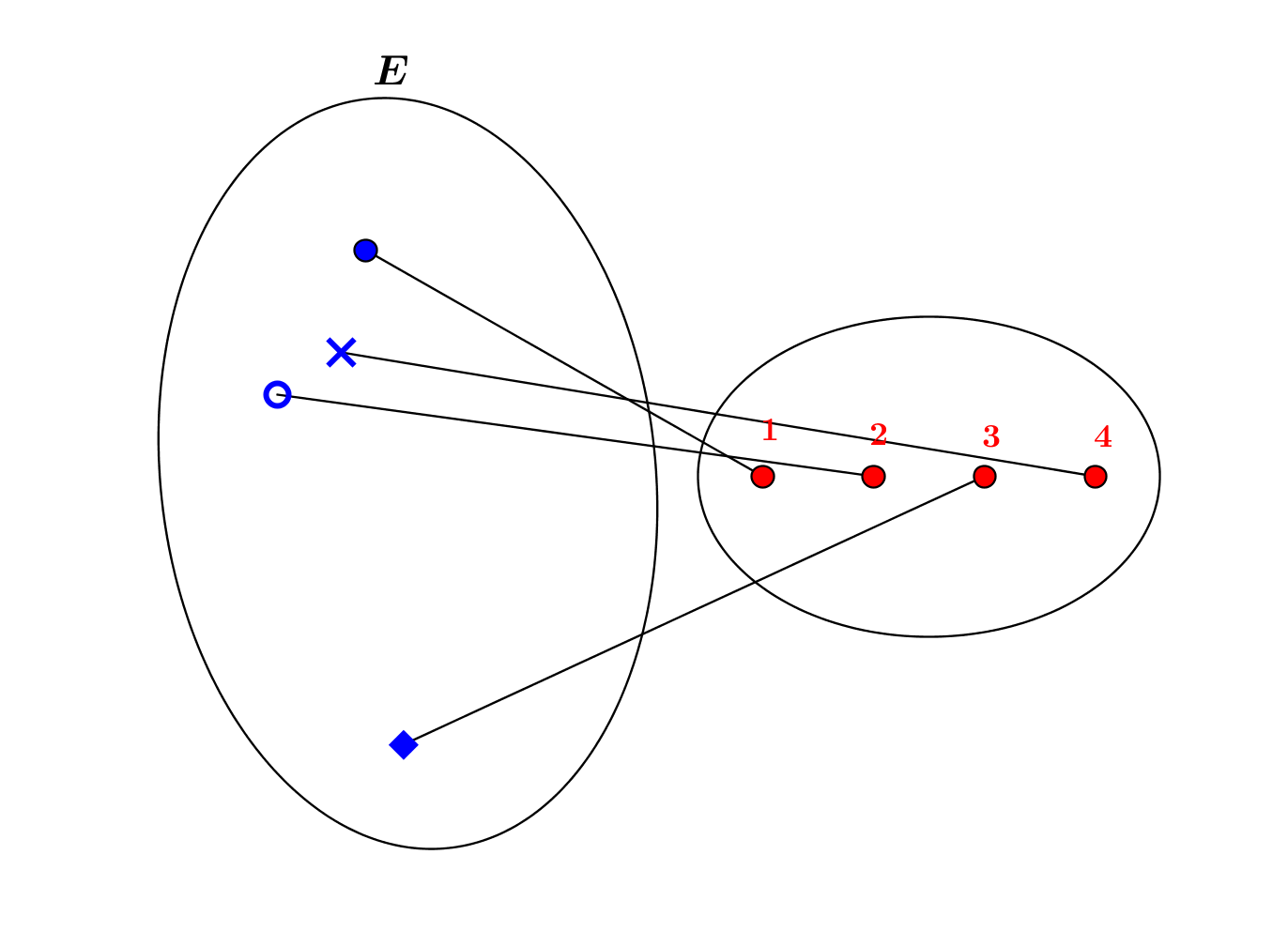
On dénombre l’ensemble \(E\) en utilisant le même principe de la bijection : on associe un-à-un les éléments de \(E\) aux premiers entiers naturels, jusqu’à avoir associé tous ses éléments : l’ensemble \(E\) est en bijection avec l’ensemble \(\{1,2,3,4\}\), il possède donc \(4\) éléments.
3. Le premier des ensembles infinis
3.1. Définition des ensembles infinis
Bienvenue sur La Règle et le Compas ! Pour lire les articles du blog en intégralité, merci de vous connecter. Si ce n'est déjà fait, vous pouvez vous inscrire librement ici sur MATHESIS.
Pour aller plus loin
La notion d’infini est structurante pour toutes les mathématiques et se définit de manière élémentaire
> Cours d’Introduction aux Fonctions et à l’Infini Mathématique – MATHESIS I.2
Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :

La notion d’infini mathématique est basée sur des axiomes. Elle se base sur une logique raisonnable contrairement aux notions religieuse et philosophique pour qui l’infini n’a ni début ni fin. En mathématique il y a toujours une origine et les infinis sont des itérations avec un début, une règle et un infini donc axiome et temps « mathématique ». L’Hôtel de Hilbert est une pirouette: il est semi borné. L’ajout de chambres est contraire à l’axiome même d' »origine ». JR
Certaines notions d’infini n’ont ni début ni fin. C’est le cas des ordres linéaires sans extrémités, comme pour l’ensemble $\mathbb Z$ des entiers relatifs, et les infinis philosophiques peuvent reposer sur une logique saine (voir par exemple J. Cohn, « Histoire de l’infini »).
Si par « l’axiome d’origine » vous faites référence à l’axiome de l’infini en théorie des ensembles, il n’est pas question de début ou de fin. Mais quoiqu’il en soit, l’ajout de chambres dans l’hôtel de Hilbert ne contredit pas l’infinité méréologique présentée ici, puisqu’il exprime précisément que l’ensemble $\mathbb N$ est en bijection avec une partie propre de lui-même, ici l’ensemble des nombres pairs et celui des nombres impairs.
Bonjour, Tout d’abord, je précise que mon niveau en mathématique s’arrête au collè-ge, donc, je ne saurai discuter des relations mathématiques, mais seulement au niveau du raisonnement.
Ici, je ne saisi pas le raisonnement tenu avec l’hotel de Hilbert, car si l’énoncé dit qu’il y a une infinité de chambres toutes déjà occupées au moment où arrive le bus, alors, il n’y a aucune chambre vide pouvant se libérer, car cela viole l’énoncé. Tel que posé, on ne peut pas séparer la chambre et son occupant, pour cela, il faut que l’énoncé le permette. Ici, il y a bijection entre les chambres et les occupants. Les deux sont intriqués par l’énoncé et forment donc un couple fini s’étendant dans l’infini. Qui a pour conséquence qu’on se retrouve avec le principe des tiroirs de Dirichlet.
,
Pour pouvoir accueillir de nouveaux clients, il faut qui’il existe une infinité de chambres déjà occupées, mais auxquelles on peut ajouter une infnité de chambres non occupées. Donc, que les deux infinis ne soient pas liés. Ce qui respecte alors strictement ce que vous écrivez.
Bref, je ne remet pas en cause le développement, mais l’énoncé qui, de ce point de vue, comporte un biais de logique causale qui nuit à la clarté du raisonnement. En tous les cas, le mien !
Mais peut être avez vous une explication qui invalide mon raisonnement et dans ce cas là, merci de me le faire connaître.
Bonjour,
Je ne sais pas ce que vous appelez ici « relations mathématiques », mais il est impossible de séparer le raisonnement mathématique des concepts qu’il emploie.
Je ne suis pas certain non plus de saisir votre raisonnement concernant l’impossibilité de faire sortir les occupants de chaque chambre; ce n’est toutefois pas un élément significatif, ce qui compte ici c’est d’établir une bijection (c’est-à-dire une correspondance un-à-un) entre certains ensembles.
En effet, la logique mathématique n’est pas causale, mais elle repose sur la description formelle des objets mathématiques par des ensembles : l’articulation entre les deux est expliquée dans [Mathesis I.1 : Entrer dans l’univers mathématique]. > voir https://reglecompas.fr/mathesis-i-1
Dans cet article tous les aspects ne sont bien sûr pas expliqués, mais essayons de préciser l’exemple.
Les chambres de l’hôtel sont numérotées par les entiers naturels 0,1,2,… . Au début, l’hôtel est complet : on peut donc numéroter chaque client par la chambre qu’il occupe : le n°0 dans la chambre 0, le n°1 dans la chambre 1, et ainsi de suite : on a une bijection entre les chambres et les clients.
Pour libérer autant de chambres qu’il y en a (!), on demande alors aux clients de sortir de leur chambre, et de changer de chambre. Le client 0 peut rester dans sa chambre, le client 1 doit passer de la chambre 1 à la chambre 2, le 3 à la chambre 6, etc… : le client numéro $n$ soit aller s’installer dans la chambre numéro $2n$. Il y aura toujours assez de place pour les premiers clients puisqu’il y a ainsi une bijection entre nombres entiers naturels et nombres pairs.
Ainsi, les chambres de numéro impair ont toutes été libérées. Si on numérote cette fois les clients qui arrivent en bus, en partant de 0 et par tous les entiers naturels 0,1,2,3,…, on peut leur assigner à chacun une chambre libre : on attribue au (nouveau) client 0 la chambre 1, au client 1 la chambre 3, au client 2 la chambre 5, etc… : le nouveau client numéro $n$ doit s’installer dans la chambre numéro $2n+1$. Il y a de la place pour eux tous, puisqu’on a ainsi aussi une bijection entre les entiers naturels, et les entiers impairs !
Peut-être pouvez-vous essayer de faire un dessin, où sur une ligne vous placez quelques points pour les chambres, numérotées, sur une seconde ligne quelques clients numérotés, sur une troisième clients quelques nouveaux clients numérotés, et tâcher d’attribuer aux uns et aux autres la chambre qui leur convient.
Ou bien, si vous êtes gêné par la « libération » des chambres, modifiez l’exemple comme suit : deux bus arrivent au même hôtel, contenant chacun autant de passagers qu’il y a d’entiers naturels. Les chambres paires de l’hôtel sont d’un côté du couloir, les chambres impaires de l’autre : comment loger les deux bus dans l’hôtel, en plaçant les clients de chaque bus du même côté ?
Quoiqu’il en soit, il n’y a pas de problème dans la logique sous-jacente à cet exemple classique, et qui exploite simplement la notion de bijection entre un ensemble infini, ici l’ensemble $\mathbb N$, et deux de ses sous-ensembles propres, ici l’ensemble $2\mathbb N$ des entiers naturels pairs, et l’ensemble $2\mathbb N +1$ des entiers naturels impairs.
Ces propriétés étranges de l’infini mathématique sont abordées dans [Mathesis I.2 : Ensembles, Applications et Numération]. > voir https://reglecompas.fr/mathesis-i-2
Merci pour votre réponse et vos liens, mais je ne crois pas que mon intérêt pour le monde mathématique soit suffisant, ici, seule la cohérence entre l’énoncé et le développement m’intéressait car mon centre d’intérêt est la logique causale, mais pas exactement comme vous la connaissez.
Ceci, car de mon point de vue toute science repose sur la causalité, sans cela, il n’y a pas de science possible. Mais pour en faire la démonstration un simple commentaire ne saurait suffire. D’ailleurs, si la causalité n’était pas au coeur des mathématiques, on ne pourrait pas faire de raisonnement mathématiques. Par contre, cela peut produire des aberrations de logique causale.
Ici, je n’écris pas qu’un occupant ne peut pas sortir de sa chambre ou en changer, mais que selon l’énoncé, toutes les chambres sont occupées à l’infini et de ce fait, occupent déjà les sous ensembles pairs et impairs et ne peuvent pas libérer des chambres car cela impliquerait de « dupliquer » l’ensemble des nombres entiers dans le même espace temps. Ce qui est possible avec un autre hotel, mais pas le même. C’est un peu comme vouloir jouer deux parties d’échecs en même temps sur un même plateau.
Je comprends parfaitement que vous pouvez vous affranchir d’une cohésion parfaite avec la causalité car il s’agit d’un hotel imaginaire fait pour appuyer ou présenter le développement mathématique et que c’est accessoire.
Pour vous donner un aperçu de la logique causale telle que suivi par moi, elle repose (entre autres) sur trois sous principes disons exécutoires que sont la récurrence, l’itération et la fractalisation ou fractale. Toutes les trois intriquées.
Appliqué à l’ensemble des nombres entiers naturels, cela donne une suite infini de 1 pour la récurrence, donc, où la numérotation des positions des additions de 1 (donnant 1;2;3…) sont le fait de l’itération et où la fractalisation consiste à changer d’échelle, donc, passer des opérations d’additions et soustractions à celles de multiplications et de divisions. L’échelle supérieure étant les nombres complexes. Comme je m’intéresse qu’aux éléments de bases, je ne suis pas allé plus loin, bien incapable de le faire !
Ici, une des lois fondamemtales de la causalité dit qu’un principe est fondamentalement (dans ses conditions d’existences) invariant quelle que soit l’échelle ou le domaine auquel on l’applique, seule sa forme change et radicalement par changement d’échelle ou de domaine. Pour comprendre comment ce changement s’effectue il convient d’étudier la géométrie des fractales. Chose que je n’ai faites qu’à la marge, uniquement pour voir le principe.
En tous les cas, merci pour l’échange et si vous voulez en savoir plus sur ce que j’entend par logique causale, je suis ouvert au débat sous un autre lien. D’autant que cela touche directement à la philosophie et même la religion, ceci, car la causalité pose le principe selon lequel l’être en tant que tel, c’est à dire, doué de volonté est défini par la finalité, le but qu’il se propose d’atteindre, mais pas des moyens qui sont le domaine exclusif, totalitaire de la causalité et d’elle seule.
Bref, la fin ne justifie pas les moyens (sauf lorsqu’il y a le choix) mais les nécessites…