La dérivée d’une fonction, c’est sa variation instantanée, autrement dit la pente de la tangente à la représentation graphique de la fonction en ce point

1. Idée générale : une variation instantanée

On se place ici dans le cadre des fonctions d’une variable réelle, disons des fonctions \(f:I\to \mathbb R\) définies sur un intervalle ouvert \(I\) de \(\mathbb R\) et à valeurs dans \(\mathbb R\). \(I\) est donc un ensemble de la forme \(]a,b[=\{x\in \mathbb R : a<x<b\}\), pour \(a<b\) des nombres réels ou l’un des symboles \(-\infty\) ou \(+\infty\). Dire qu’une telle fonction \(f:I\to\mathbb R\) est dérivable en un point \(t\in I\), c’est dire intuitivement que cette fonction \(f\) possède une « variation instantanée au point \(t\) ». Quand c’est le cas, cette variation instantanée, étant un nombre réel noté \(f'(t)\), possède donc un signe (positif ou négatif), qui nous donne le sens de la variation, et une magnitude (sa valeur absolue \(|f'(t)|\)), qui nous donne l’intensité de la variation.

2. Taux d’accroissement, rapport de monotonie et dérivée

2.1. Rapport de monotonie et interprétation géométrique

Pour préciser la notion de dérivée, il nous faut définir la variation de la fonction \(f\) entre deux points. Le point \(t\in I\) étant donné, si \(x\in I\) est un autre point la variation de \(f\) entre \(t\) et \(x\) est le rapport de la variation entre \(t\) et \(x\) et de la variation entre les valeurs \(f(t)\) et \(f(x)\) de \(f\) en ces deux points. Ce taux d’accroissement de \(f\) entre \(t\) et \(x\), appelé mathématiquement rapport de monotonie, est donc le rapport \(\frac{f(x)-f(t)}{x-t}\) (on suppose que \(x\neq t\), pour pouvoir diviser par \(x-t\)). Le rapport de monotonie possède une interprétation géométrique simple : il s’agit de la pente de la droite joignant le point de coordonnées \((t,f(t))\) et le point de coordonnées \((x,f(x))\), situés sur le graphe (représentation graphique) de la fonction \(f\).

Sur la figure suivante, nous avons représenté en rouge le graphe de la fonction carré \(f(x)=x^2\), et placé deux points : \(A\), de coordonnées \((t,t^2)\) (c’est-à-dire \((t,f(t))\)) et \(B\) de coordonnées \((x,x^2)\) (c’est-à-dire \((x,f(x))\)).

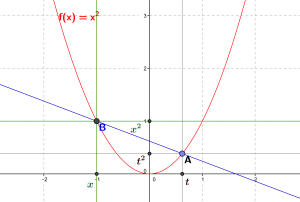
La droite représentée en bleu joint les points \(A\) et \(B\), et sa pente est le rapport de monotonie \(\frac{f(x)-f(t)}{x-t}\), soit ici \(\frac{x^2-t^2}{x-t}\) (qui vaut \(x+t\) d’après l’identité remarquable \(x^2-t^2=(x-t)(x+t)\)).

2.2. Variation instantanée et dérivée en point

Si on assimile les abscisses (c’est-à-dire les valeurs de la variable) au « temps », la variation représentée par le rapport de monotonie s’effectue « sur un certain temps ». La notion de dérivée de \(f\) en \(t\) comme variation « instantanée » considère alors ce temps comme « infiniment petit » : cela correspond aux valeurs du rapport de monotonie, c’est-à-dire de la pente de la droite joignant les points \((t,f(t))\) et \((x,f(x))\), « lorsque \(x\) se rapproche indéfiniment du point fixe \(t\). Mathématiquement, ceci s’interprète comme la recherche de la limite du rapport \(\frac{f(x)-f(t)}{x-t}\) « lorsque \(x\) tend vers \(t\) » (\(t\) étant fixé, et \(x\neq t\)). Ainsi, la fonction \(f\) est dite dérivable en \(t\) si la limite \(\lim\limits_{x\to t}\frac{f(x)-f(t)}{x-t}\) existe, et cette limite est alors par définition la dérivée de la fonction \(f\) en \(t\).

3. Fonction dérivée

Géométriquement, on peut alors considérer la dérivée \(f'(t)\) comme la limite de la pente de la droite joignant \((t,f(t))\) et \((x,f(x))\) lorsque \(x\) se rapproche de \(t\), autrement dit comme la pente de la droite obtenue pour \(x=t\), soit la pente de la droite tangente au graphe de \(f\) au point \((t,f(t))\). Sur la figure suivante, nous avons repris la représentation graphique de la fonction \(f(x)=x^2\) et de la droite joignant le point fixe \(A\) de coordonnées \((t,f(t))\) et le point mobile \(B\) de coordonnées \((x,f(x))\), que nous déplaçons en fonction des valeurs de \(x\). 

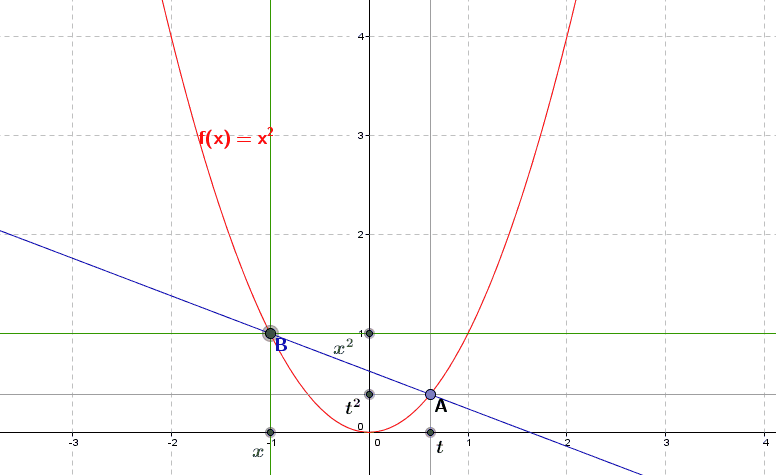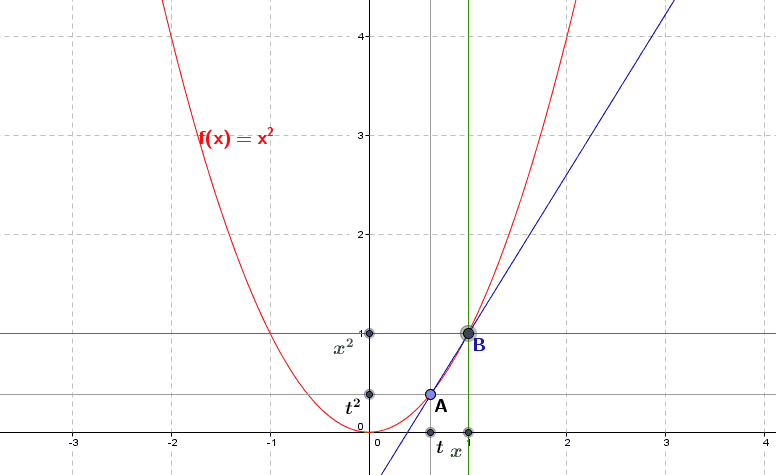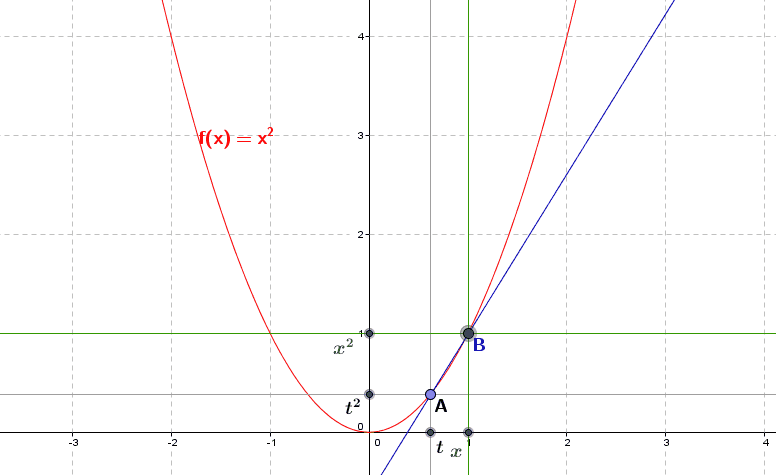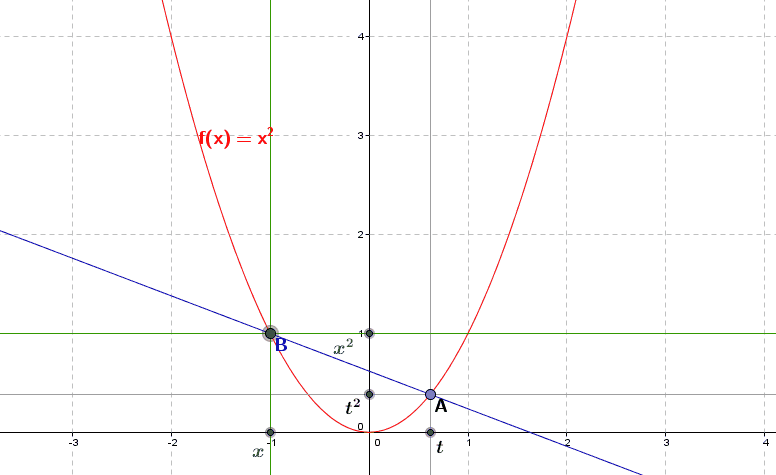
Nous observons que lorsque l’abscisse \(x\) du point \(B\) se rapproche de l’abscisse \(t\) du point \(A\), et la droite se rapproche de la droite tangente au point \(A\), que \(x\) soit \(<t\) ou que \(x\) soit \(>t\). La recherche de la limite du rapport de monotonie inclut en effet les deux cas où \(x>t\) (lorsque \(x\) est à droite de \(t\)) et où \(x<t\) (lorsque le point \(x\) est à « gauche » de \(t\).

2.3. Résumé : dérivée d’une fonction en un point

Pour résumer :

•  lorsque \(f\) est dérivable en \(t\in I\), le rapport de monotonie \(\frac{f(x)-f(t)}{x-t}\) se rapproche d’un taux d’accroissement \(f'(t)\) correspondant à des valeurs de \(x\) de plus en plus proches de \(t\)
• géométriquement, la pente de la droite joignant les points \((t,f(t))\) et \((x,f(x))\) se rapproche de la pente de la tangente au graphe de la fonction \(f\) au point \((t,f(t))\), qui est la dérivée \(f'(t)\)
• La dérivée \(f'(t)\) de \(f\) au point \(t\) est donc la « variation instantanée » de la fonction \(f\), analogue de la « vélocité » d’une trajectoire.

3.1. Fonction dérivée d’une fonction dérivable

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :