Quand il s’agit de compter ou de classer des ensembles, nous faisons appel à deux types de nombres : les ordinaux et les cardinaux. Alors que les nombres ordinaux nous aident à mettre en ordre une série d’éléments (premier, deuxième, troisième, etc.), les nombres cardinaux indiquent combien il y a d’éléments dans un ensemble. Mais comment définissons-nous précisément ces nombres cardinaux? L’approche historique de Frege et Cantor les perçoit à travers une relation spéciale entre ensembles appelée « équipotence ». Cependant, von Neumann nous offre une autre perspective en les assimilant à certains nombres ordinaux. Explorons cette distinction fascinante.

1.Comment définir des quantités infinies ?

1.1.Le problème des quantités infinies

Si les nombres ordinaux permettent d’énumérer, grâce à l’axiome du choix, n’importe quel ensemble – fini ou infini – nous avons constaté qu’au contraire des ensembles finis, des énumérations différentes pouvaient conduire à des résultats différents pour des ensembles infinis. Ainsi, alors que les nombres ordinaux et cardinaux finis sont en quelque sorte identiques, les nombres ordinaux infinis ne peuvent pas servir à définir sans ambiguÏté le « nombre d’éléments » d’un ensemble infini, et donc d’un ensemble en général : nous devons nous tourner vers une « autre » sorte de nombre, le nombre cardinal.

1.2.Revenir au « nombre d’éléments » : l’équipotence

La première manière de concevoir les nombres cardinaux consiste à revenir à la définition du « nombre d’éléments », ou plutôt, comme nous l’avons souligné à propos de l’infini mathématique, de ce que signifie que deux ensembles $E$ et $F$ ont « le même nombre d’éléments ». Cela advient si, et seulement si, on peut apparier un-à-un les éléments de $E$ et de $F$, autrement dit s’il existe une bijection (c’est-à-dire une correspondance bi-univoque ou « un-à-un ») entre $E$ et $F$ : on dit alors que $E$ et $F$ sont « équipotents » (littéralement ont la même « puissance », vocabulaire de Cantor). Il n’est donc pas même besoin de savoir définir « le nombre d’éléments » d’un ensemble, pour pouvoir dire que deux ensembles ont le même nombre d’éléments ! A partir de cette seule notion d’équipotence, nous pouvons donner une définition du « nombre » cardinal.

Exemple 1
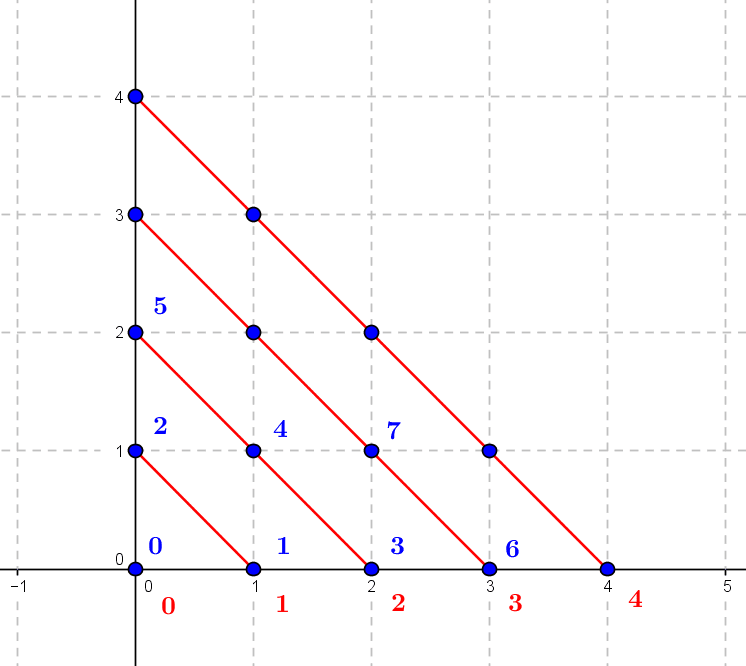
i) Contrairement aux ensembles finis non vides, l’ensemble infini $\mathbb N$ des entiers naturels est équipotent à son carré cartésien $\mathbb N\times\mathbb N$. Par exemple, on démontre que l’application $f:(p,q)\in\mathbb N^2\mapsto \frac{(p+q)(p+q+1)}{2}+q\in\mathbb N$ est une bijection (voir la figure 1). Ainsi, $\mathbb N$ et $\mathbb N\times\mathbb N$ ont le même nombre d’éléments, donc le même cardinal.
ii) On peut montrer qu’il existe de même des bijections entre $\mathbb N$ et les ensembles $\mathbb Z$ des entiers relatifs et $\mathbb Q$ des nombres rationnels : même si cela contrevient à l’intuition, ils doivent donc tous le même cardinal.
iii) En revanche, on démontre en utilisant les développements des nombres réels positifs dans une base numérique entière (voir Plus de réels que de rationnels), que si on peut inclure l’ensemble $\mathbb N$ dans l’ensemble $\mathbb R$ des nombres réels, il n’existe toutefois pas de bijection du premier sur le second : le nombre cardinal de $\mathbb R$ devrait être différent de celui de $\mathbb N$.

2.L’approche logique et ensembliste historique

2.1.Définir le nombre à partir de la logique

C’est cette approche qu’a choisie Gottlob Frege, mathématicien et philosophe, dans ses Fondements de l’Arithmétique où il cherchait à inclure l’arithmétique élémentaire dans la philosophie, reconstruisant les nombres entiers à partir de la seule logique. Son approche, malgré quelques difficultés soulevées par ses contemporains, était essentiellement correcte et profondément visionnaire, et nous pouvons ici l’adopter pour exposer une version primitive de la notion de cardinal, en introduisant le vocabulaire des ensembles de Georg Cantor, ainsi que la distinction d’avec les classes (voir Le paradoxe de Russell et la théorie des classes).

2.2.Le nombre cardinal selon Frege et Cantor

L’idée essentielle de Frege et de Cantor, c’est ainsi de définir un nombre cardinal comme une classe d’ensembles « ayant tous le même nombre d’éléments » :

Définition 1
Le nombre d’éléments d’un ensemble $E$ est la classe de tous les ensembles $F$ qui sont équipotents à $E$.

Autrement dit, le cardinal de $E$ « au sens de Frege-Cantor », est la classe de tous les ensembles $F$ pour lesquels il existe une bijection entre $E$ et $F$. On définit ainsi « le nombre d’éléments » à partir de la relation « avoir le même nombre d’éléments », mais il n’y a pas ici de circularité, puisque cette notion d’équipotence ne fait usage que du concept ensembliste de bijection. Et puisqu’on s’est autorisé à distinguer entre les classes et les ensembles, ce « nombre cardinal » $N$ de $E$ ne pose pas de problème de définition, les éléments de $N$ étant des ensembles.

Exemple 2
i) Les ensembles $\mathbb N$, $\mathbb Z$ et $\mathbb Q$, étant tous équipotents, sont tous éléments du nombre cardinal de $\mathbb N$ au sens présent.
ii) Le nombre cardinal de l’ensemble $\mathbb R$ – qui n’est pas équipotent aux ensembles précédents – est différent du précédent. On montre que l’ensemble $2^{\mathbb N}$ des suites de $0$ et de $1$ (voir Plus de réels que de rationnels) est équipotent à $\mathbb R$ et possède donc le même nombre cardinal; c’est aussi le cas de l’ensemble $\mathbb R^{\mathbb N}$ des suites de nombres réels, puisqu’on peut le mettre en bijection avec $(2^{\mathbb N})^{\mathbb N}$ et donc avec $2^{\mathbb N\times\mathbb N}$ : on conclut à l’aide de la bijection entre $\mathbb N^2$ et $\mathbb N$ de l’exemple 1.
iii) Si deux ensembles $E$ et $F$ n’ont pas le même nombre d’éléments, par définition leurs nombres cardinaux sont des classes disjointes (sans élément en commun).

3.L’approche scientifique moderne de la théorie des ensembles

3.1.La monstruosité des classes cardinales

Une telle conception du nombre cardinal est similaire à celle – plus complexe en fait – que nous avons introduite à propos du nombre ordinal comme « classe de bons ordres équivalents » à un bon ordre donné. Elle est parfaitement rigoureuse, mais peu maniable sur le plan arithmétique, celui du calcul avec les quantités infinies, qui est devenu aussi naturel et commun en théorie des ensembles que le calcul avec les entiers l’est dans la mathématique classique. En effet, les nombres cardinaux ainsi conçus sont (excepté pour le cas très particulier du « nombre » $0$, qui est la classe $\{\emptyset\}$ puisqu’il n’existe qu’un seul ensemble ne contenant aucun élément…) des classes propres, c’est-à-dire des multiplicités colossales dont la taille excède celle de tout ensemble, et que Cantor appelait « absolument infinies ». Le maniement de tels objets est très limité, et il est par exemple impossible de définir l’exponentiation de deux cardinaux, comme on le fait pour les nombres finis : si ces « nombres » convenaient donc au foisonnement initial de la logique mathématique moderne, il fallait toutefois leur trouver une contrepartie plus maniable, et plus proche de l’intuition de ce qu’est un nombre.

3.2.Définir le nombre cardinal comme un ensemble de même taille

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :