A partir de la fonction exponentielle complexe, on peut définir une fonction « exponentielle circulaire », qui « enroule » la droite réelle sur le cercle trigonométrique, et permet de définir rigoureusement les fonctions trigonométriques cosinus et sinus, qui s’étendent à tout le plan complexe, et de démontrer leurs propriétés élémentaires.

Introduction : définir les fonctions trigonométriques

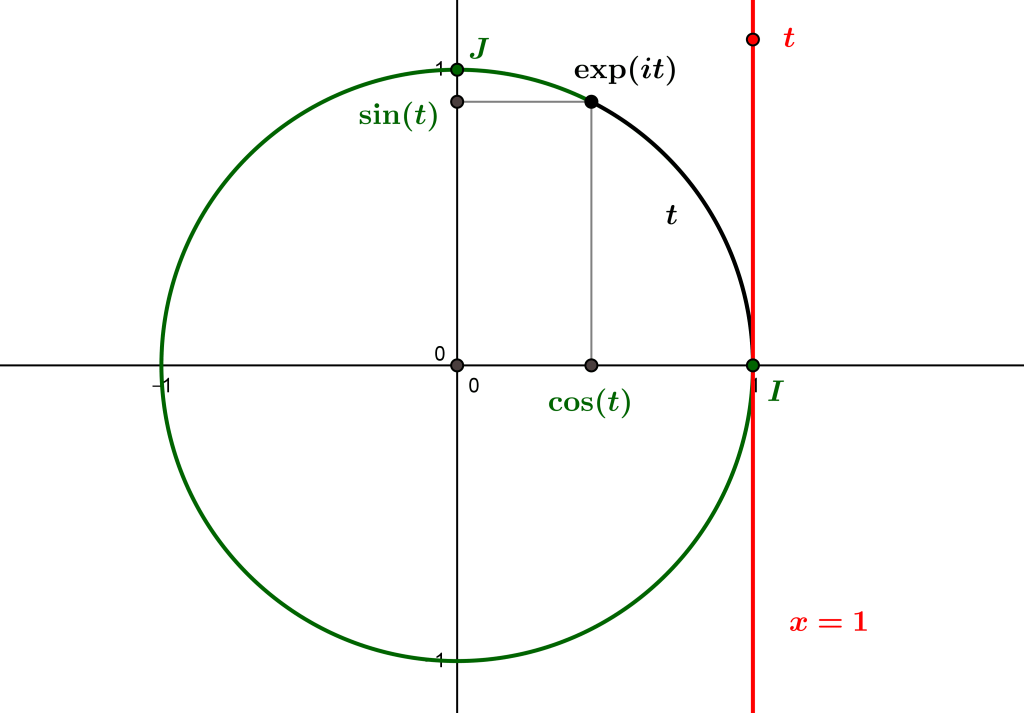
Nous avons évoqué dans « Le cercle trigonométrique : où Pythagore rencontre Thalès » les fonctions trigonométriques cosinus et sinus, qui se définissent rigoureusement de manière géométrique pour des angles (orientés). Leur définition comme fonctions \(\cos : \mathbb R\to \mathbb R\) et \(\sin:\mathbb R\to \mathbb R\) est plus délicate, et nous n’en avons donné pour l’instant qu’une explication intuitive, correspondant à « l’enroulement » de la droite réelle sur le cercle trigonométrique. 

Les fonctions cosinus et sinus d’une variable réelle sont appelées fonctions circulaires, et nous les définirons rigoureusement ici grâce à la fonction que nous appellerons exponentielle « circulaire », et que nous introduirons à partir de l’exponentielle complexe. Nous retrouverons les propriétés usuelles de \(\cos\) et \(\sin\) à partir de cette fonction, et ce sera l’occasion d’introduire la représentation et la notation trigonométriques des nombres complexes.

1.L’exponentielle « circulaire »

Définition à partir de l’exponentielle complexe

La fonction analytique \(\exp:\mathbb C\to \mathbb C^*\) est définie pour tout nombre complexe \(z\in\mathbb C\) comme la somme de la série convergente \(\sum \dfrac{z^n}{n!}\). Cette fonction prolonge en fait la fonction exponentielle réelle \(\exp:\mathbb R\to \mathbb R_+^*\) (voir Fonctions analytiques et exponentielle complexe), et si on en considère la restriction à l’ensemble \(i\mathbb R=\{z\in\mathbb C : \exists x\in\mathbb R,\ z=ix\}\) des nombres imaginaires purs, on définit une nouvelle fonction, que nous appelons exponentielle « circulaire ».

Pour être plus précis, la fonction à laquelle nous faisons référence est l’application \(e\) définie sur l’ensemble \(\mathbb R\), et à valeurs dans \(S^1=\{z\in\mathbb C : |z|=1\}\) des nombres complexes de module \(1\), par \(e(t)=\exp(it)\). Nous avons vu en effet en étudiant l’exponentielle complexe que pour tout nombre imaginaire pur \(z=x+iy\), on a \(|\exp(z)|=1\). Le cercle \(S^1\) n’étant autre que le cercle trigonométrique, la fonction \(e\) n’est autre que « l’enroulement » de la droite réelle sur ce cercle, à partir duquel nous avons évoqué une définition possible des fonctions cosinus et sinus. 

Propriétés de \(e:t\mapsto \exp(it)\)

Avant de tirer de cette fonction une définition rigoureuse du cosinus et du sinus, nous en explicitons quelques propriétés élémentaires, tirées des propriétés de l’exponentielle complexe.

Le cercle trigonométrique \(S^1\) est « stable » par la multiplication : si \(z,w\in S^1\) sont deux nombres complexes de module \(1\), leur produit \(z.w\) est également de module \(1\). Comme l’exponentielle complexe est un « homomorphisme de groupes » de \((\mathbb C,+)\) dans \((\mathbb C^*,\times)\), cela signifie que l’exponentielle circulaire transforme l’addition des nombres réels en la multiplication des nombres complexes de module \(1\). Autrement dit, si \(s,t\) sont deux nombres réels, on a \(e(s+t)=\exp(i(s+t))=\exp(is+it)=\exp(is)\times\exp(it)=e(s)\times e(t)\) : la fonction \(e\) est elle-même un homomorphisme de groupes, du groupe \((\mathbb R,+)\) dans le groupe \((S^1,\times)\).

Comme fonction de \(\mathbb R\) dans \(\mathbb C\), l’application \(e\) est une fonction de \(\mathbb R\) dans \(\mathbb R^2\) et comme telle, elle est dérivable en tant que fonction analytique. En particulier, elle est continue, et une expression de sa dérivée est alors donnée à partir de sa série dérivée, et puisqu’on a \(e(t)=\sum_{n=0}^{+\infty} \dfrac{(it)^n}{n!}=\sum_{n=0}^{+\infty} \dfrac{i^n}{n!} t^n\), cette série nous donne la valeur de \(e'(t)\), soit \(\sum_{n=0}^{+\infty} (n+1)\dfrac{i^{n+1}}{(n+1)!} t^n=i\sum_{n=0}^{+\infty} \dfrac{i^n}{n!} t^n=ie(t)\). Cette formule nous sera utile pour dériver le cosinus et le sinus réels.

2.Définition et propriétés du cosinus et du sinus

Une définition rigoureuse des fonctions \(\cos\) et \(\sin\)

Une fois défini cet « enroulement » de la droite réelle sur le cercle trigonométrique, qu’est l’exponentielle circulaire, la définition des fonctions circulaires est immédiate. On définit le cosinus d’un nombre réel quelconque \(t\) comme la partie réelle de \(e(t)=\exp(it)\), et le sinus de \(t\) comme la partie imaginaire de \(e(t)\). En composant ainsi la fonction \(e:\mathbb R\to \mathbb C\) par les fonctions partie réelle \(Re:\mathbb C\to \mathbb R,\ x+iy\mapsto x\) et partie imaginaire \(Im:x+iy\in\mathbb C\mapsto y\in \mathbb R\) – qui ne sont que les deux projections du plan euclidien, on obtient deux fonctions, le cosinus \(\cos:\mathbb R\to \mathbb R\) et le sinus \(\sin:\mathbb R\to \mathbb R\). 

A partir de la définition de \(e:\mathbb R\to \mathbb C\) comme fonction analytique et des propriétés de la partie réelle et de la partie imaginaire de la somme d’une série de nombres complexes, on peut alors donner une description du cosinus et du sinus comme sommes de séries. En effet, puisque pour tout nombre réel \(t\), on a \(e(t)=\exp(it)=\sum_{n=0}^{+\infty} \dfrac{(it)^n}{n!}\), en utilisant le fait que \(i^{2n}=(-1)^n\) et \(i^{2n+1}=(-1)^ni\) pour tout entier naturel \(n\), il vient \[\cos(t)=Re(e(t))=\sum_{n=0}^{+\infty} (-1)^n\dfrac{t^{2n}}{(2n)!}\] et \[\sin(t)=Im(e(t))=\sum_{n=0}^{+\infty} (-1)^n\dfrac{t^{2n+1}}{(2n+1)!},\] ce qui signifie que les fonctions \(\cos\) et \(\sin\) sont des fonctions analytiques réelles.

Retrouver les propriétés des fonctions trigonométriques

A partir des propriétés de l’exponentielle circulaire, il est possible d’établir rigoureusement les propriétés élémentaires des fonctions \(cos\) et \(sin\) réelles. Pour cela, il suffit désormais de représenter la fonction \(e\) à partir des fonctions \(\cos\) et \(\sin\) : en effet, pour tout nombre réel \(t\), nous pouvons désormais écrire \(e(t)=\exp(it)=\cos t+i\sin t\), par définition ! Par exemple, pour tous réels \(s,t\) on a \[\cos(s+t)+i\sin(s+t)=\exp(i(s+t))=\exp(is)\exp(it)=(\cos s+i\sin s).(\cos t+i\sin t).\] En prenant la partie réelle des deux membres extrêmes on obtient \(cos(s+t)=\cos s\cos t-\sin s\sin t\). En prenant les parties imaginaires cette fois-ci, on obtient également \(\sin(s+t)=\sin s \cos t+\sin t\cos s\) : on retrouve les identités trigonométriques fondamentales.

Nous avons déjà dérivé la fonction \(e\), et nous pouvons maintenant écrire pour tout \(t\in\mathbb R\), \[e'(t)=ie(t)=i\exp(it)=i(\cos t+i\sin t)=-\sin t+i\cos t.\] Or, la dérivée d’une fonction de \(\mathbb R\) dans \(\mathbb R^2\) s’obtient en dérivant chaque coordonnée. Puisque la fonction \(e\) se représente comme \(t\in\mathbb R\mapsto (\cos t,\sin t)\), on en tire directement l’expression des dérivées des fonctions \(\cos t\) et \(\sin t\). En effet, on a \(e'(t)=(\cos’t,\sin’t)\), d’où \(\cos’ t=-\sin t\) et \(\sin’t=\cos t\), ce qu’on peut retrouver en dérivant les séries représentant \(\cos\) et \(sin\) comme fonctions analytiques ! Notons que la norme de \(e'(t)\) est \(||e'(t)||=\sqrt{(-\sin t)^2+(\cos t)^2}=1\), si bien que la longueur de l’arc déterminé par \(I\) et \(\exp(it)\) est \(\int_0^t ||e'(x)||\ dx=\int_0^t dx=t\).

3.Les fonctions circulaires complexes

Exprimer \(\cos t\) et \(\sin t\) en fonction de \(\exp(it)\)

A partir de l’écriture \(\exp(it)=\cos t+i\sin t\), on peut donner des expressions de \(\cos t\) et \(\sin t\) en fonction de \(\exp(it)\). En effet, pour tout nombre complexe \(z=x+iy\), on sait que \(x=Re(z)=\frac 1 2 (z+\overline z)\) et \(y=Im(z)=\frac 1 {2i} (z-\overline z)\). Or, le conjugé \(\overline z=x-iy\) d’un nombre complexe \(z=x+it\) de la forme \(z=\exp(it)\) est \(\overline z=\exp(-it)\) : il s’ensuit que l’on a \[\cos t=Re(\exp(it))=\dfrac{\exp(it)+\exp(-it)}{2}\] et \[\sin t=Im(\exp(it))=\dfrac{\exp(it)-\exp(-it)}{2i}.\].

Prolonger le cosinus et le sinus à l’ensemble \(\mathbb C\)

Or, rien n’empêche, dans cette expression, de remplacer le nombre réel \(t\) par un nombre complexe quelconque \(z\) : on définirait ainsi deux fonctions de \(\mathbb C\) dans \(\mathbb C\), appelées encore « cosinus » et « sinus » (complexes), et définies par \[\cos z=\dfrac{\exp(iz)+\exp(-iz)}{2}\] et \[\sin z=\dfrac{\exp(iz)-\exp(-iz)}{2i}.\] Attention : dans le cas général, les relations à la partie réelle et la partie imaginaire de \(z\) sont plus compliquées. Ces fonctions pourraient également être définies à partir des développements en série entière écrits précédemment, qui s’étendent à des séries convergentes sur tout le plan complexe, à savoir \[\cos(z)= \sum_{n=0}^{+\infty} (-1)^n\dfrac{z^{2n}}{(2n)!}\] et \[\sin(z)=\sum_{n=0}^{+\infty} (-1)^n\dfrac{z^{2n+1}}{(2n+1)!}\] pour tout nombre complexe \(z\). On voit donc de deux manières différentes que les fonctions \(\cos,\sin:\mathbb C\to \mathbb C\) sont analytiques.

De telles fonctions, comme l’exponentielle complexe, analytiques et définies sur l’ensemble \(\mathbb C\) tout entier, sont dites entières. Or, le théorème de Liouville nous dit qu’une fonction entière et bornée est constante. Les fonctions cosinus et sinus n’étant pas constantes, elles ne sont donc pas bornées ! Autrement dit, alors que le cosinus et le sinus d’un nombre réel sont toujours compris entre \(-1\) et \(1\) (ce sont les coordonnées d’un point du cercle trigonométrique), le cosinus et le sinus d’un nombre complexe peuvent prendre des valeurs arbitrairement grandes !

Pour aller plus loin

Commencer en mathématiques : Mathesis I.1 – Entrer dans l’Univers Mathématique