Introduction

Dans Angles de vecteurs : intuition géométrique et définition algébrique, nous avons défini et décrit le groupe des angles de vecteurs du plan euclidien de manière algébrique, en utilisant une relation d’équivalence sur les vecteurs unitaires. De même qu’on peut mesurer des longueurs, on apprend à l’école élémentaire qu’on peut mesurer des angles. Nous présentons ici les fondements de la mesure des angles de vecteurs, dont l’unité mathématique est le radian (voir aussi Le cercle trigonométrique : où Pythagore rencontre Thalès), à partir de l’analyse réelle et complexe.

1.Mesurer les angles par l’exponentielle circulaire

Si \(\vec\alpha=[(\vec u,\vec v)]\) est un angle de vecteurs, de sorte que \(\vec u,\vec v\) sont deux vecteurs unitaires, on sait qu’il existe une unique rotation vectorielle \(r\) telle que \(r(\vec u)=\vec v\). Par définition, l’angle \(\vec\alpha\) est l’angle de la rotation \(r\), laquelle s’écrit sous la forme \(r(x,y)=(ax+by,-bx+ay)\) pour tout vecteur \((x,y)\in\mathbb R^2\), avec \(a^2+b^2=1\). Rappelons d’ailleurs que le point \((a,b)\), vu comme vecteur unitaire \(\vec{u’}\), donne la représentation standard de l’angle \(\vec\alpha=[(\vec i,\vec{u’})]\), avec \(\vec i=(0,1)\).

Or, puisque le point \((a,b)\) est ainsi sur le cercle trigonométrique, il est l’image par la fonction exponentielle circulaire \(e(t)=\exp(it)\) d’un nombre réel \(t\). En effet, pour des raisons liées à sa continuité et à l’étude élémentaire des fonctions cosinus et sinus, cette fonction de \(\mathbb R\) dans \(S^1\) est en fait surjective. Autrement dit : il existe un nombre réel \(t\) tel que \[a+ib=(a,b)=\exp(it).\] Par définition, un nombre réel \(t\) tel que \(\exp(it)=(a,b)\) est une mesure de l’angle de vecteurs \(\vec\alpha\). 

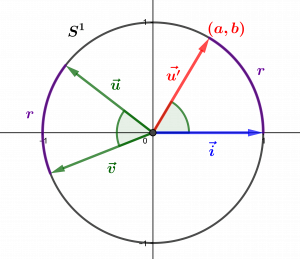
L’angle \(\vec\alpha=[(\vec u,\vec v)]\) entre les vecteurs \(\vec u\) et \(\vec v\) est mesuré grâce à la rotation \(r\) qui envoie \(\vec u\) sur \(\vec v\). La même rotation envoie \(\vec i =(0,1)\) sur \(\vec{u’}=(a,b)\), et il existe \(t\in\mathbb R\) tel que \(\exp(it)=a+ib=(a,b)\) : \(t\) est une mesure de \(\vec\alpha\).

2.Une mesure « à \(2\pi\) près » d’après la définition de \(\pi\)

Un tel nombre réel \(t\) possède donc la propriété suivante : on a \(\exp(it)=(a,b)=(\cos t,\sin t\)). Or, on peut démontrer qu’il existe un plus petit nombre réel \(t>0\) tel que \(\cos t=0\); si on note ce nombre \(a\), on peut définir le nombre \(\pi\) comme \(2a\). Pour tout nombre réel \(t\) on a alors \(\cos(t+2\pi)=\cos(t)\) et \(\sin(t+2\pi)=\sin(t)\) – on dit que le nombre \(2\pi\) est la période des fonctions cosinus et sinus. On peut donc encore écrire \((a,b)=\exp(it)=(\cos(t),\sin(t))=(\cos(t+2\pi),\sin(t+2\pi))=\exp(i(t+2\pi))\) !

En d’autres termes, si \(t\) est une mesure de l’angle \(\vec\alpha\) – obtenue par \(e(t)\) grâce au point \((a,b)\) associé à la rotation \(r\) d’angle \(\vec\alpha\) – alors \(t+2\pi\) est une autre mesure du même angle. Intuitivement, puisque la fonction \(e(t)\) « enroule » la droite réelle sur le cercle trigonométrique, et que le périmètre du cercle est \(2\pi\), on ne change pas l’angle en ajoutant \(2\pi\), ou un multiple entier de \(2\pi\), à sa mesure. En somme, il existe plusieurs mesures possibles d’un angle de vecteurs.

3.Le « noyau » de l’exponentielle circulaire

Pour aller plus loin