L’approche analytique de la géométrie plane, que nous devons à Descartes, permet de donner une description purement algébrique des droites du plan comme ensembles de solutions d’équations d’un seul type. Ces équations dites cartésiennes contiennent toute l’information géométrique des droites, et permettent d’en donner plusieurs représentations et de définir le parallélisme à partir du concept vectoriel de direction.

1.La représentation analytique d’une droite : les équations cartésiennes

1.1.De la droite comme objet intuitif à la géométrie cartésienne

Qu’est-ce qu’une droite dans le plan ? La géométrie euclidienne classique, celle de l’Antiquité, considère que les points et les droites du plan sont des objets de l’intuition, des concepts primitifs qu’on ne définit pas, et précise plutôt à travers un petit nombre d’axiomes comment points et droites sont liés, ce qui permet d’en fonder la théorie mathématique de manière rigoureuse. Par exemple, le fameux « cinquième postulat d’Euclide », appelé aussi « axiome des parallèles » , et dont la remise en question a donné naissance au 19ième siècle aux géométries dites « non euclidiennes », est formulé de manière simple par le mathématicien Proclus au 5ième siècle de notre ère sous la forme suivante :

« Dans un plan, par un point distinct d’une droite, il existe une et une seule droite parallèle à cette droite. »

Ici, la notion de parallélisme est celle de deux droites distinctes qui n’ont aucun point d’intersection. Or, avec l’avènement de l’approche analytique de la géométrie cartésienne (voir Le plan euclidien), qui réduit grâce à l’introduction de coordonnées la géométrie du plan à l’algèbre des nombres réels, toutes ces notions se définissent grâce à la théorie des ensembles à partir de celles de point ou de vecteur (deux manières duales de considérer les éléments du plan euclidien $\mathbb R^2$, c’est-à-dire les couples $(x,y)$ de nombres réels). Les axiomes de la géométrie euclidienne classique deviennent donc des définitions ou des théorèmes !

1.2.Une définition simple d’une droite du plan, et sa traduction analytique

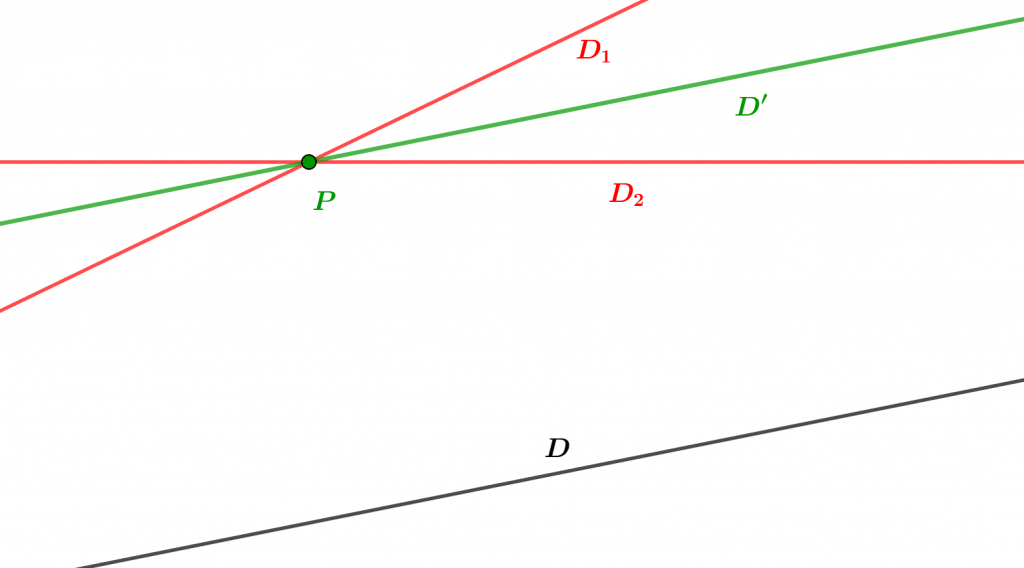
Intuitivement, une droite (affine) du plan euclidien est donc pour nous un certain sous-ensemble $D$ de $\mathbb R^2$ qui doit posséder deux propriétés essentielles : trois points quelconques de $D$ doivent être alignés, et $D$ doit pouvoir être « prolongée indéfiniment » dans les deux sens. Dans le langage de la géométrie cartésienne, ces propriétés se formulent comme suit :

1. Si $M,N$ et $P$ sont trois points de $D$ (c’est-à-dire trois éléments du sous-ensemble $D$), ils sont alignés, autrement dit les vecteurs $\vec{MN}=N-M$ et $\vec{MP}=P-M$ sont colinéaires (c’est-à-dire proportionnels)
2. Si $M$ et $N$ sont deux points distincts de $D$, alors :
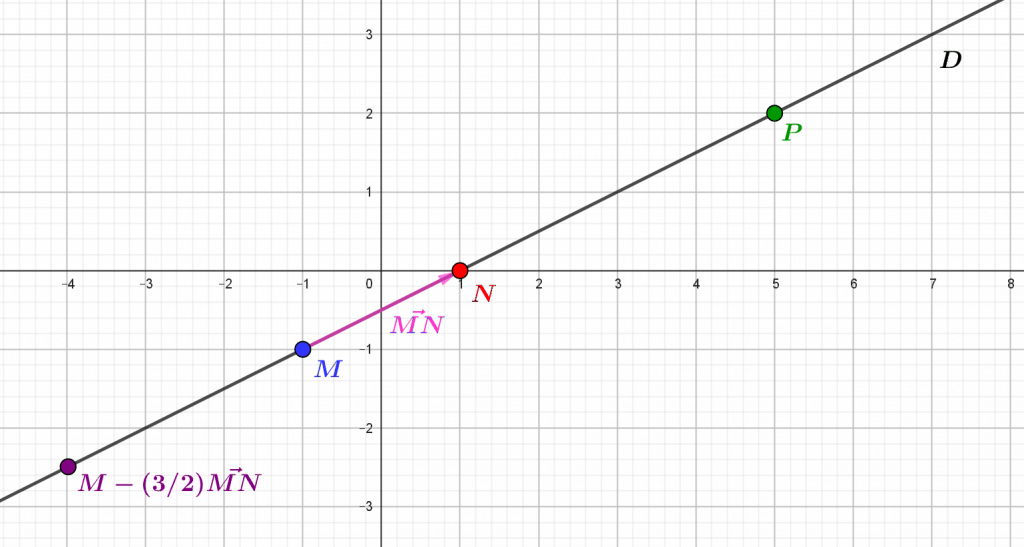
   • Si $\lambda$ ($\lambda$= »lambda », onzième lettre de l’alphabet grec) est un nombre réel, alors le point $M+\lambda\vec{MN}$ est aussi sur $D$ ($\vec{MN}$ est le « vecteur $M,N$ », c’est-à-dire $N-M$)
   • Si $P$ est un point de $D$, alors $P$ est la forme précédente, autrement dit il existe un nombre réel $\lambda$ tel que $P=M+\lambda\vec{MN}$.

Dans cette formulation, on voit déjà apparaître l’interaction entre les notions duales de point et de vecteur. Une droite vectorielle est alors une droite $D$ qui passe par l’origine, autrement dit telle que le point $O=(0,0)$ est sur $D$. Or, à partir de deux points $M=(a,b)$ et $N=(c,d)$ distincts d’une droite donnée $D$, et de leur coordonnées, on peut extraire une équation de la forme $(E)\ a’x+b’y+c’=0$ (où $a’=b-d$, $b’=c-a$ ne sont pas tous deux nuls et où $c’=ad-bc$), et qui détermine entièrement la droite $D$, au sens où les solutions de $(E)$, c’est-à-dire les points $(x,y)$ du plan tels que $a’x+b’y+c’=0$, sont exactement les points de $D$. Ainsi, toute droite du plan se décrit comme ensemble de solutions d’une équation, dite cartésienne, et réciproquement l’ensemble des solutions de toute équation cartésienne, c’est-à-dire de la forme $(E)$ avec $a’$ ou $b’$ non nul, est une droite. On a donc une description intégrale des droites du plan sous une forme algébrique.

2.La direction d’une droite du plan : points et vecteurs

2.1.Définir la direction d’une droite affine

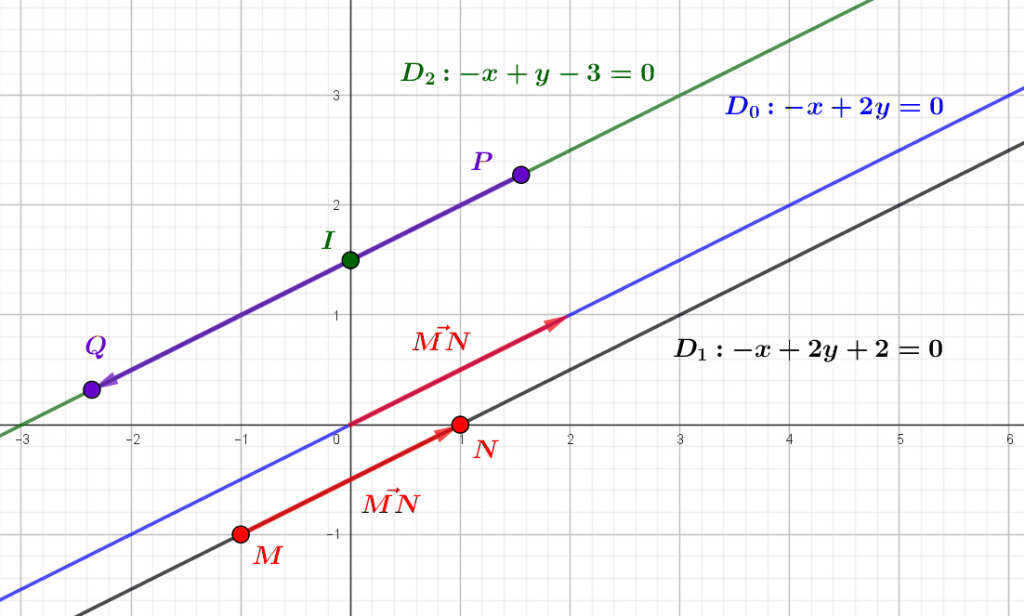
Nous pouvons ainsi abandonner la définition précédente d’une droite (affine) comme sous-ensemble du plan ayant les propriétés 1 et 2, pour la définition analytique (en termes de coordonnées), c’est-à-dire comme sous-ensemble des solutions d’une équation de la forme $(E)\ ax+by+c=0$, avec $a\neq 0$ ou $b\neq 0$ (ou les deux), où $c$. Une telle droite est alors vectorielle si et seulement si $O=(0,0)$ est solution de l’équation $(E)$, autrement dit si et seulement $a.0+b.0+c=0$, c’est-à-dire $c=0$. Les droites vectorielles sont donc les ensembles de solutions des équations de la forme $ax+by=0$, avec $a\neq 0$ ou $b\neq 0$. En général, si $D$ est la droite d’équation $(E)\ ax+by+c=0$, on appelle direction de $(D)$ la droite vectorielle $D_0$ d’équation $ax+by=0$. On dit alors qu’une droite $D’$ est parallèle à $D$ si c’est l’ensemble des solutions d’une équation de la forme $(E’)\ ax+by+c’=0$, autrement dit si $D$ et $D’$ ont la même direction. On appelle aussi vecteur directeur de $D$ tout vecteur non nul $u=(p,q)$ qui « donne la direction de $D$ », autrement dit tout élément non nul de la direction $D_0$ de $D$. En particulier, l’équation $(E)$ donne immédiatement comme vecteur directeur le vecteur $(-b,a)$, puisque $a.(-b)+b.a=-a.b+b.a=0$, et que $a\neq 0$ ou $b\neq 0$ ! Deux droites parallèles ont évidemment les mêmes vecteurs directeurs. En fait, si $M$ et $N$ sont deux points de $D$, ils vérifient l’équation $(E)$, donc le vecteur $\vec{MN}=N-M$ vérifie l’équation $(E_0)\ ax+by=0$, qui est celle de la direction de $E$ : c’est donc un vecteur directeur de $D$. Enfin, si une droite vectorielle $D_0$ est donnée par une équation cartésienne $(E_0)\ ax+by=0$, alors la droite $D$ de direction $D_0$ et passant par un point $M=(u,v)$ a pour équation $(E)\ ax+by+c=0$, avec $c=-(au+bv)$, puisque $(u,v)$ est une solution de $(E)$ !

2.2.Détermination vectorielle de l’équation d’une droite