Il existe diverses manières de définir les nombres complexes. La plus directe consiste à les regarder comme les points ou les vecteurs du plan. L’addition et la multiplication se définissent alors grâce aux coordonnées.

1. L’ensemble \(\mathbb C\) des nombres complexes

1.1. Un nombre complexe est un nombre à deux dimensions

Un nombre complexe est tout simplement un vecteur ou un point du plan euclidien \(\mathbb R^2=\mathbb R\times \mathbb R\) (voir Le Plan euclidien : géométrie antique et approche analytique). Autrement dit, c’est un couple \((a,b)\) de nombre réels, c’est-à-dire un nombre « à deux dimensions ». Quand on le considère comme nombre complexe, c’est qu’implicitement on le considère comme intégré à une structure algébrique particulière sur \(\mathbb R^2\).

1.2. L’addition et la multiplication des nombres complexes

Soyons plus précis : cette « structure » consiste en une addition vectorielle et une multiplication complexe (c’est-à-dire géométrique). Pour l’addition vectorielle, si \((a,b)\) et \((c,d)\) sont deux vecteurs du plan \(\mathbb R^2\), alors par définition on les additionne « coordonnée-par-coordonnée », c’est-à-dire que \((a,b)+(c,d)=(a+c,b+d)\). Au sujet de la multiplication complexe, au lieu de multiplier « coordonnée-par-coordonnée », on multiple comme suit : \((a,b).(c,d)=(ac-bd,ad+bc)\). Cette multiplication correspond géométriquement à ce qu’on appelle une similitude plane (définie par le nombre \((a,b)\) et appliquée au nombre \((c,d)\)), qui est une transformation du plan préservant la « forme » des objets (d’où le terme de « similitude », de l’adjectif « similaire »). Comme dans l’ensemble \(\mathbb R\) des nombres réels, l’addition et la multiplication sont associatives et commutatives (on peut les faire dans n’importe quel sens). Aussi, la multiplication est distributive sur l’addition : si \((a,b), (c,d)\) et \((e,f)\) sont des nombres complexes, on a \((a,b).((c,d)+(e,f))=(a,b).(c,d)+(a,b).(e,f)\), ce qu’on peut vérifier à partir de la définition.

1.3. Le « corps » des nombres complexes

En termes savant, on dit qu’on ne considère pas seulement sur \(\mathbb R^2\) la structure « d’espace vectoriel produit », ni la structure « d’anneau produit », mais une « structure d’anneau » qu’on note \(\mathbb C\). Le « zéro » pour l’addition est le nombre \((0,0)\) (origine géométrique du plan), puisque \((a,b)+(0,0)=(a,b)\) pour tout nombre complexe \((a,b)\in\mathbb C\). Le « un » pour la multiplication est le nombre \((1,0)\), puisque \((a,b).(1,0)=(a.1–0.0,a.0+b.1)=(a,b)\) par définition. Cette structure est ce qu’on appelle un corps : tout élément non nul possède un inverse, ce qu’on peut voir comme suit. Si \((a,b)\in\mathbb C\) n’est pas nul, alors soit \(a\neq 0\) soit \(b\neq 0\) et dans les deux cas, on a \(a^2+b^2\neq 0\), et alors \((a,b).(\dfrac{a}{a^2+b^2},-\dfrac{b}{a^2+b^2})=(\dfrac{a^2+b^2}{a^2+b^2},\dfrac{-ab+ba}{a^2+b^2})=(1,0)\), si bien que \((\dfrac{a}{a^2+b^2},-\dfrac{b}{a^2+b^2})\) est l’inverse de \((a,b)\) !

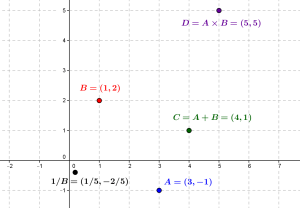
Sur la figure suivante, nous avons représenté deux points du plan, \(A\) et \(B\), considérés comme nombres complexes, ainsi que leur somme \(C=A+B\) et leur produit (complexe) \(D=A\times B\). Le point \(1/B\) est l’inverse complexe de \(B\).

2. Partie réelle et partie imaginaire

2.1. Une racine carrée imaginaire de \(-1\)

Pour bien expliquer ce qu’ils sont, nous n’avons pas présenté d’emblée les nombres complexes avec leur notation habituelle, que nous introduisons maintenant grâce à une justification algébrique. Une particularité de ces nombres est qu’il existe un nombre complexe \((a,b)\) tel que \((a,b)^2=-1\) (!), autrement dit une « racine carrée de \(-1\)« . Lorsque nous écrivons ceci, nous avons identifié le nombre (réel) \(-1\) avec le nombre complexe \((-1,0)\) : on identifie en fait chaque nombre réel \(a\) avec le nombre complexe \((a,0)\). On dit qu’on a un homomorphisme de corps de \(\mathbb R\) dans \(\mathbb C\) et géométriquement, cela revient à considérer la « droite réelle » \(\mathbb R\) (voir Qu’est-ce qu’un nombre réel ?) comme l’axe des abscisses. La « racine carrée » \((0,1)\) de \(-1\) se trouve alors « hors » de l’ensemble \(\mathbb R\), on dit qu’elle est « imaginaire » !

2.2. Notation habituelle des nombres complexes

Il existe en fait deux nombres complexes dont le carré vaut \(-1\), le nombre \((0,1)\) et le nombre \((0,-1)\), ce qu’on peut vérifier par exemple pour le premier en calculant \[(0,1)^2=(0,1).(0,1)=(0.0–1.1,0.1+1.0)=(-1,0).\] Le nombre complexe \((0,1)\) est noté \(i\), et à cause de cette propriété algébrique, il est beaucoup plus commode, sur les plans algébrique et géométrique, d’écrire un nombre complexe de la forme \((a,b)\) sous la forme \(a+ib\), ce qui est la notation \(a.1+b.i=a.(1,0)+b.(0,1)\). En effet, on peut multiplier un nombre complexe \((a,b)\) quelconque par un nombre réel \(c\) donné comme suit, en le considérant comme un vecteur : \(c.(a,b)=(ca,cb)\). Il s’ensuit que le vecteur \(a+ib=a.1+b.i\) est exactement \(a.(1,0)+b.(0,1)\) par l’identification des nombres réels, ou encore \((a,0)+(0,b)=(a,b)\).

2.3. Partie réelle, partie imaginaire, affixe

Pour aller plus loin

Les nombres complexes font partie des ensembles naturels fondamentaux, à la racine de la théorie mathématique > Cours d’Introduction à la Mathématique Supérieure – MATHESIS I.1

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :