La multiplication complexe se prolonge naturellement à une multiplication en quatre dimensions, qui définit sur l’espace \(\mathbb R^4\) la structure de l’algèbre \(\mathbb H\) des quaternions de Hamilton. Cette multiplication s’interprète géométriquement à partir du produit scalaire et du produit vectoriel dans l’espace, ce qui permet de séparer une composante « scalaire » et une composante « vectorielle », faisant de \(\mathbb H\) un « espace-temps algébrique ».

1.La définition algébrique des quaternions

1.1.Retrouver la multiplication complexe à partir de \(i^2=-1\)

Lorsque l’on définit la structure algébrique des nombres complexes, on prolonge de manière géométrique la structure de l’ensemble \(\mathbb R\) à celle de l’ensemble \(\mathbb C\). Ce prolongement consiste à définir une « multiplication vectorielle » sur le plan \(\mathbb R^2\), distributive sur l’addition habituelle des vecteurs coordonnée par coordonnée. Le nombre complexe \((0,1)\), noté \(i\), joue un rôle essentiel dans la description algébrique des nombres complexes, puisqu’un tel nombre peut s’écrire sous la forme \((a,b)=a+ib\). La « règle » \(i^2=-1\) permet alors de retrouver la multiplication complexe à partir des propriétés habituelles du produit, sous la forme \[(a+ib).(c+id)=ac+i(ad+bc)+i²(bd)=ac-bd+i(ad+bc).\]

1.2.Prolonger la structure complexe en dimension supérieure

Le mathématicien et physicien irlandais William Rowan Hamilton souhaitait étendre les nombres complexes en dimension supérieure. Alors qu’il cherchait désespérément une opération analogue à la multiplication complexe en trois dimensions, la solution lui vint en 1843 sous la forme d’une intuition au cours d’une promenade en compagnie de son épouse. Il fallait réfléchir en quatre dimensions pour multiplier des vecteurs de dimension supérieure ! Les vecteurs de l’espace \(\mathbb R^4\) sont les quadruplets de nombres réels \((t,x,y,z)\), et ils s’écrivent donc comme combinaisons des vecteurs de base notés \(1=(1,0,0,0)\), \(i=(0,1,0,0)\), \(j=(0,0,1,0)\) et \(k=(0,0,0,1)\), sous la forme \((t,x,y,z)=t.1+x.i+y.j+z.t\). L’intuition de Hamilton a consisté à deviner ou inventer les formules \[i^2=j^2=k^2=ijk=-1,\] et à découvrir qu’on pouvait définir une multiplication vectorielle en dimension \(4\) à partir des règles de multiplication des vecteurs de base. Ces règles sont : \(i²=j²=k²=-1\), \(ij=k=-ji, jk=i=-kj\) et \(ki=j=-jk\), et on les étend aux vecteurs de \(\mathbb R^4\) en écrivant \((t,x,y,z)\times (t’,x’,y’,z’)=(t.1+x.i+y.j+z.k)\times (t’.1+x’.i+y’.j+z’.k)\), soit \((tt’-xx’-yy’-zz’).1+(tx’+xt’+yz’-zy’).i+(ty’+yt’+zx’-xz’).j+(tz’+zt’+xy’-yx’).k\) en utilisant les propriété habituelles du produit.

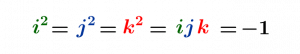
L’équation gravée par William Hamilton sur le Brougham Bridge (Dublin) en 1843, exprimant la multiplication quaternionique sur les vecteurs de base de l’espace \(\mathbb R^4\)

2.L’algèbre \(\mathbb H\) des quaternions

2.1.Une algèbre à divisions en dimension 4

Ainsi, on peut définir une multiplication en dimension \(4\), en suivant une idée analogue à celle qui permet de définir la multiplication complexe en dimension \(2\). On retrouve cette multiplication complexe pour les vecteurs de la forme \((t,x,0,0)=t.1+x.i\), qu’on identifie aux vecteurs \((t,x)\) du plan (nombres complexes \(t+xi\)), et on la prolonge ici grâce aux vecteurs \(j\) et \(k\). Cependant, cette multiplication en \(4\) dimensions, distributive sur l’addition des vecteurs, n’est plus commutative : contrairement à la multiplication complexe, il n’est pas vrai que si \(q\) et \(q’\) sont deux vecteurs de dimension \(4\), on ait toujours \(q\times q’=q’\times q\). Autrement dit, l’ordre dans lequel on effectue l’opération a une influence sur le résultat, ce qui se voit déjà sur les vecteurs de base, puisque \(i\times j=-j\times i\), \(j\times k=-k\times j\) et \(k\times i=-i\times k\). L’ensemble \(\mathbb R^4\), avec son addition vectorielle et cette multiplication, est appelé algèbre des quaternions (de Hamilton), et notée \(\mathbb H\). Le vecteur \(1=(1,0,0,0)\) est le « un » de cette multiplication, au sens où si \(q=(t,x,y,z)\) est un quaternion, on a \(1\times q=q\times 1=q\), ce qu’on peut vérifier facilement par le calcul. De plus, comme dans \(\mathbb Q\), \(\mathbb R\) et \(\mathbb C\), tout élément non nul \(q\) de \(\mathbb H\) possède un unique inverse \(q^{-1}\), c’est-à-dire tel que \(q\times q^{-1}=q^{-1}\times q=1\). On dit que \(\mathbb H\) est un corps non commutatif ou en général une algèbre à divisions.

2.2.Interprétation géométrique : un espace-temps algébrique