Le produit scalaire et le déterminant sont des concepts clés de l’algèbre linéaire dans le plan euclidien, offrant une compréhension profonde des relations entre deux vecteurs $u$ et $v$. Lorsque ces vecteurs sont unitaires, leur produit scalaire et déterminant correspondent respectivement au cosinus et au sinus de l’angle qu’ils forment, permettant ainsi un calcul direct de ces valeurs trigonométriques à partir de leurs coordonnées. Cette approche analytique nous mène à une interprétation géométrique du déterminant : il représente l’aire algébrique du parallélogramme « orienté » formé par les deux vecteurs dans le plan.

1.Cosinus et sinus de deux vecteurs

1.1.Rappel : cosinus et sinus d’un angle orienté

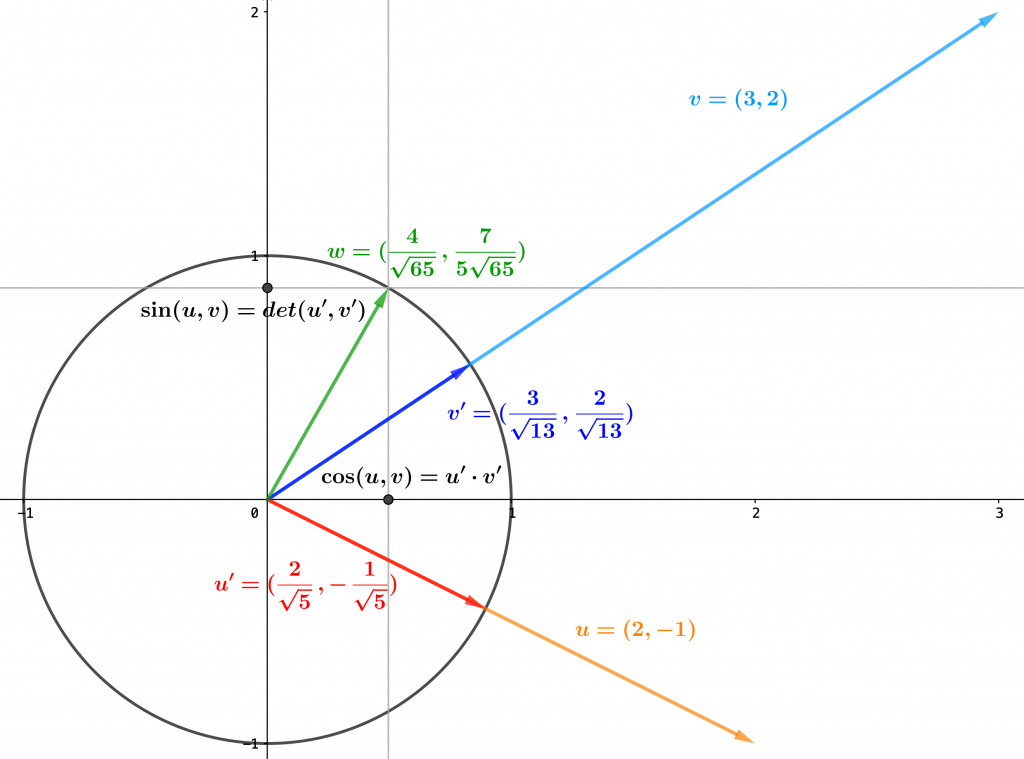
En introduisant les angles orientés, nous avons défini les coordonnées circulaires, c’est-à-dire le cosinus et le sinus, de ces angles de vecteurs, à partir de leur représentation standard. Cela revient, étant donnés deux vecteurs unitaires $u$ et $v$ (c’est-à-dire de norme $1$), à considérer l’unique rotation vectorielle $r$ qui envoie $u$ sur $v$ : une telle rotation est de la forme $r:(x,y)\mapsto (ax-by,bx+ay)$ pour des nombres réels uniques $a,b$ tels que $a^2+b^2=1$ (voir Rotations vectorielles du plan). Par définition, le cosinus de l’angle orienté $\alpha=[(u,v)]$ déterminé par $(u,v)$ est le nombre $a$, tandis que le nombre $b$ est le sinus de $\alpha$ : on retrouve ici $\cos\alpha$ et $\sin\alpha$ comme les coordonnées du point $(a,b)$ qui représente $r$ sur le cercle trigonométrique, ou encore $w$ dans la représentation standard $[(i,w)]$ de $\alpha$, c’est-à-dire tel que $w=r(i)$, pour $i=(1,0)$ le premier vecteur de la base canonique. Nous avons alors identifié le cosinus et le sinus d’un tel angle de manière purement analytique, c’est-à-dire à partir des seules coordonnées des vecteurs $u=(a_1,b_1)$ et $v=(a_2,b_2)$, à travers les formules remarquables suivantes :

• $\cos [(u,v)]=a_1a_2+b_1b_2=u\cdot v$ (produit scalaire de $u$ et $v$)
• $\sin[(u,v)]=a_1b_2-a_2b_1=det(u,v)$ (déterminant de $u$ et $v$).

1.2.Angle formé par deux vecteurs non nuls

Puisque deux vecteurs unitaires définissent un angle orienté, c’est aussi le cas de deux vecteurs non nuls $u$ et $v$ quelconques. En effet, on obtient deux vecteurs $u’$ et $v’$ de norme $1$ en divisant $u$ et $v$, respectivement, par leur norme, c’est-à-dire en posant $u’=u/||u||$ et $v’=v/||v||$, ce qu’on peut faire puisque $u$ et $v$ ne sont pas nuls. Or, la demi-droite dirigée selon $u’$ est la demi-droite dirigée selon $u$, et de même la demi-droite dirigée selon $v’$ est la demi-droite dirigée selon $v$ : on peut donc parler sans ambiguïté de l’angle déterminé par le couple de vecteurs $(u,v)$ :

Définition 1
Si $u$ et $v$ sont deux vecteurs non nuls, l’angle déterminée par le couple $(u,v)$ est l’angle de vecteurs $[(u’,v’)]$, pour les vecteurs unitaires $u’=u/||u||$ et $v’=v/||v||$.

L’angle est orienté : il faut tenir compte de l’ordre des vecteurs, de sorte que l’angle déterminé par $(v,u)$ est l’opposé de celui qui est déterminé par $(u,v)$.

1.3.Cosinus et sinus de deux vecteurs non nuls

Etant donnés deux vecteurs non nuls $u$ et $v$, nous pouvons donc définir le cosinus de $u$ et $v$, noté $\cos(u,v)$, et le sinus de $u$ et $v$, noté $\sin(u,v)$, comme ceux de l’angle orienté déterminé par $u$ et $v$. A partir des expressions analytiques du cosinus et du sinus de deux vecteurs unitaires rappelées au premier paragraphe, nous pouvons alors donner une expression trigonométrique de leur produit scalaire et de leur déterminant , grâce aux propriétés de linéarité de ceux-ci :

Proposition 1
Si $u$ et $v$ sont deux vecteurs non nuls, alors on a :
i) $u\cdot v=||u||\times ||v|| \times \cos(u,v)$
ii) $det(u,v)=||u||\times ||v|| \times \sin(u,v).$

Pour démontrer la premier égalité, puisque $u’=u/||u||$ et $v’=v/||v||$ sont unitaires, on a $\cos(u,v)=\cos(u’,v’)=u’\cdot v’=((1/||u||)u)\cdot ((1/||v||)v)=(1/||u||)\times (1/||v||)\times (u\cdot v)$ (par linéarité du produit scalaire en $u$ et $v$), et on obtient l’égalité en multipliant chaque membre par $||u||\times |||v||$. On procède de la même manière pour la seconde, par linéarité du déterminant $det(u,v)$ en chaque composante $u,v$ également.

Si donc $u=(a,b)$ et $v=(c,d)$ sont deux vecteurs non nuls, les formules précédentes permettent de calculer immédiatement le cosinus et le sinus de l’angle qu’ils déterminent, puisque l’on a $u\cdot v=ac+bd$, $det(u,v)=ad-bc$, $||u||^2=a^2+b^2$ et $||v||^2=c^2+d^2$. On peut donc écrire :

i) $\cos(u,v)=\dfrac{ac+bd}{\sqrt{(a^2+b^2)(c^2+d^2)}}$
ii) $\sin(u,v)=\dfrac{ad-bc}{\sqrt{(a^2+b^2)(c^2+d^2)}}.$

2.Expression analytique de l’aire du parallélogramme

2.1.Retrouver l’expression du produit scalaire avec un angle non orienté

Nous avons trouvé une autre forme de la formule (i) de la proposition 1, concernant le produit scalaire, en travaillant avec des angles affines : dans Loi des cosinus et produit scalaire, nous avons en effet montré que si $ABC$ est un triangle non dégénéré, alors le produit scalaire des vecteurs $\vec{AB}$ et $\vec{AC}$ est donné par $$\vec{AB}\cdot\vec{AC}=AB.AC.\cos \widehat{BAC}.$$ Ainsi, en posant $u=\vec{AB}$ et $v=\vec{AC}$, la formule de la première section donne $$\vec{AB}\cdot\vec{AC}=u\cdot v=||u||.||v||.\cos(u,v)=AB.AC.\cos(\vec{AB},\vec{AC}).$$ Les deux formules sont quasiment identiques, à ceci près que le premier cosinus est celui d’un angle géométrique (non orienté), tandis que le second est celui d’un angle de vecteurs (orienté). Mais puisque les angles d’un triangle sont de mesure inférieur à $\pi$, les deux cosinus ont ici la même valeur, puisque le cosinus ne dépend pas de l’orientation. Il n’en est pas de même avec le sinus, pour lequel nous devons faire intervenir une interprétation du signe dans la formule (ii) de la proposition 1.

2.2.Le sinus et l’aire du parallélogramme

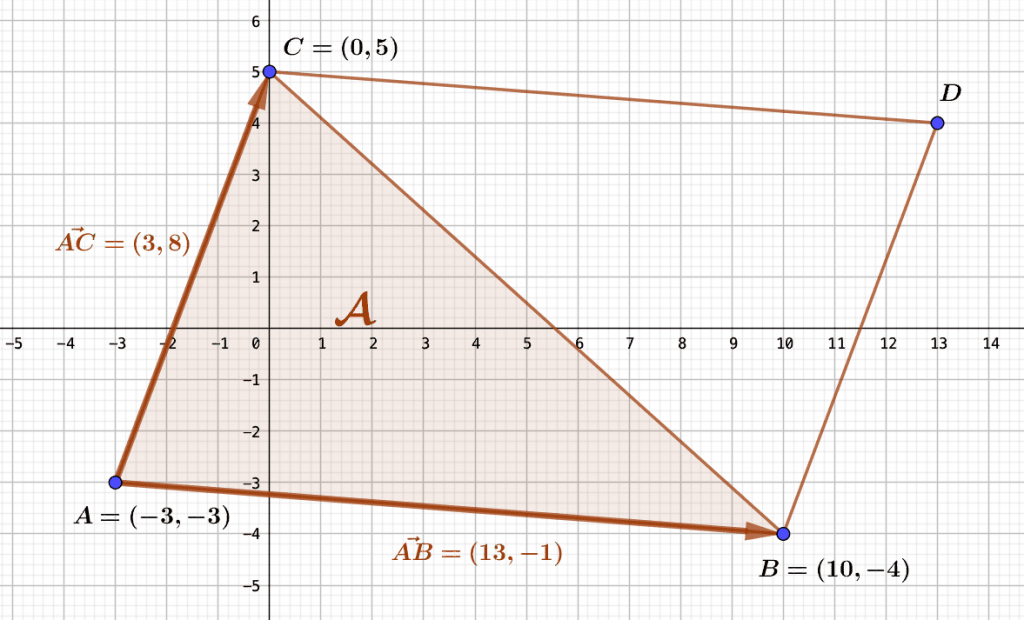
Rappelons que, de manière analogue, nous avons introduit le sinus d’un angle géométrique dans le calcul algébrique de l’aire du triangle et du parallélogramme. En effet, si $ABCD$ est un parallélogramme et $(HD)$ la hauteur du triangle $ABD$ issue de $D$, alors l’aire de $ABD$ est $(1/2).AB.HD$, si bien que l’aire de $ABCD$ est $AB.HD$ : en introduisant la loi des sinus, nous obtenons une expression trigonométrique de l’aire du triangle $ABD$ comme $(1/2).AB.AD.\sin \alpha$, où $\alpha$ est l’angle géométrique $\widehat{BAD}$, de sorte que l’aire du parallélogramme $ABCD$ est $$\mathcal A=AB.AD.\sin\widehat{BAD}.$$

Nous retrouvons ici au signe près l’expression (ii) de la proposition 1, au sens où si l’on note $u=\vec{AB}$ et $u=\vec{CD}$ les vecteurs construits à partir des côtés choisis du parallélogramme, cette expression nous donne leur déterminant sous la forme $det(u,v)=||u||.||v||.\sin(u,v)=AB.AD.\sin(\vec{AB},\vec{AD})$, où le sinus est ici celui de deux vecteurs. Or, tandis que le cosinus des vecteurs $u$ et $v$ est celui de l’angle géométrique $\widehat{BAD}$, toujours positif, le sinus des vecteurs $u$ et $v$ dépend de l’orientation, et ne s’identifie pas à celui de l’angle géométrique $\widehat{BAD}$. Autrement dit, en ajoutant une valeur absolue la seule formule que nous pouvons écrire pour l’instant à propos du déterminant et du parallélogramme est la suivante : $$\mathcal A=AB.AD.\sin\widehat{BAD}=|det(\vec{AB},\vec{AD})|.$$

3.Interprétation géométrique du déterminant

3.1.Le signe du déterminant

Afin de donner une interprétation géométrique complète du déterminant de deux vecteurs $u=(a,b)$ et $v=(c,d)$, nous devons d’abord donner le sens de son signe, positif ou négatif. Nous ne considérons ici que des vecteurs non nuls : en ce cas, le déterminant $det(u,v)$ de $u$ et $v$ est nul si et seulement si $u$ et $v$ sont colinéaires (voir Bases du plan euclidien). Autrement dit, le déterminant est non nulexactement lorsque le couple $(u,v)$ est une base du plan euclidien. Or, le signe du déterminant $det(u,v)$ change si l’on échange l’ordre de $u$ et $v$, puisqu’on a $det(v,u)=cb-da$ (par définition) $=bc-ad=-(ad-bc)=-det(u,v)$. Mais l’échange de $u$ et $v$ consiste précisément en l’inversion de l’orientation de la base $(u,v)$, puisque la base $(v,u)$ est orientée dans l’autre sens : ainsi, le signe du déterminant (non nul) de deux vecteurs non colinéaires (formant donc une base) $u$ et $v$ est la marque de l’orientation, directe ou indirecte, de la base $(u,v)$. On démontre en effet le résultat suivant :

Proposition 1
Si $u$ et $v$ sont deux vecteurs non nuls et non colinéaires, alors :
i) On a $det(u,v)>0$ si et seulement si $(u,v)$ est une base directe
ii) On a $det(u,v)<0$ si et seulement si $(u,v)$ est une base indirecte.

Souvenons-nous que la base canonique $(i,j)$ est la base définie comme référence pour les bases directes, avec $i=(1,0)$ et $j=(0,1)$ : le déterminant des vecteurs $i,j$ est bien $det(i,j)=1.1-0.0=1>0$, ce qui confirme cette proposition.

3.2.Le déterminant comme « aire algébrique »