A partir de l’approche analytique de Descartes, qui consiste à introduire des coordonnées pour représenter les points du plan, et de la construction de Cauchy des nombres réels, on peut donner une représentation moderne du plan à partir de laquelle on retrouve les axiomes géométriques d’Euclide.

1. L’approche synthétique d’Euclide (et de Hilbert)

1.1. La géométrie plane d’Euclide

Le mathématicien grec Euclide est fameux pour ses postulats et axiomes de la géométrie plane, concernant les droites, les segments, les cercles, les angles, le parallélisme, la perpendicularité… et jusqu’à aujourd’hui, on les utilise pour la géométrie du plan, concernant ces objets, et appelée précisément la géométrie euclidienne (plane). Cette approche est ce qu’on appelle en mathématique une approche synthétique : à partir d’axiomes, qui relèvent d’une formulation de l’intuition de propriétés élémentaires d’objets mathématiques, on établit des propriétés grâce à des déductions (démonstrations), ne faisant pas intervenir de calcul.

1.2. La complétion de Hilbert et la question du calcul

L’approche euclidienne, valable depuis l’Antiquité, présente toutefois certaines limites. D’une part, il manque » des axiomes pour démontrer tous les théorèmes d’Euclide (certaines démonstrations faisaient implicitement référence à des propriétés non établies), ce à quoi le mathématicien allemand David Hilbert, notamment, a remédié en 1899 en proposant une liste d’axiomes plus complète. D’autre part, dans la mathématique grecque ancienne les calculs « d’aires », comme dans le théorème de Pythagore, sont en fait des énoncés sur des recompositions de figures géométriques : l’approche synthétique n’est pas articulée au calcul, ce qui fait défaut à son interprétation dans la mathématique moderne.

D. Hilbert

2. L’approche analytique de Descartes : les coordonnées et le calcul

2.1. La méthode analytique de Descartes : les coordonnées

A l’époque moderne, le mathématicien et philosophe français René Descartes invente les « coordonnées » d’un point du plan : on peut représenter un tel point M par un couple (x,y) de nombres, x étant l’abscisse et y étant l’ordonnée du point M. Ces coordonnées correspondent aux projections du point M, perpendiculairement, sur deux « axes ».

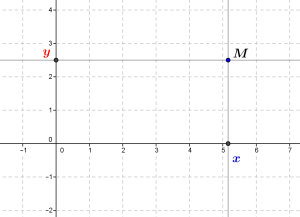
Ceci permet d’introduire le calcul dans la géométrie plane, puisqu’on peut alors par exemple représenter les droites par des équations; l’intersection de deux droites non parallèles est un point, dont on peut déterminer les coordonnées par des procédés « analytiques », c’est-à-dire ici calculatoires, à partir d’équations des deux droites ou de paramètres numériques qui les décrivent.

2.2. Les grandeurs géométriques incommensurables : utiliser les nombres réels

Cependant, si cette méthode est bien adaptée à ce qu’on appelle la « géométrie affine » (la partie de la géométrie qui a trait aux droites et au parallélisme dans ce contexte), à l’époque les nombres rationnels ne suffisent pas pour traiter de certaines grandeurs liées notamment aux triangles et aux cercles. En effet, d’après le théorème de Pythagore si nous voulons assigner une mesure de longueur à la diagonale d’un triangle rectangle, celle-ci doit être une racine carrée de la somme des carrés des longueurs des deux autres côtés.

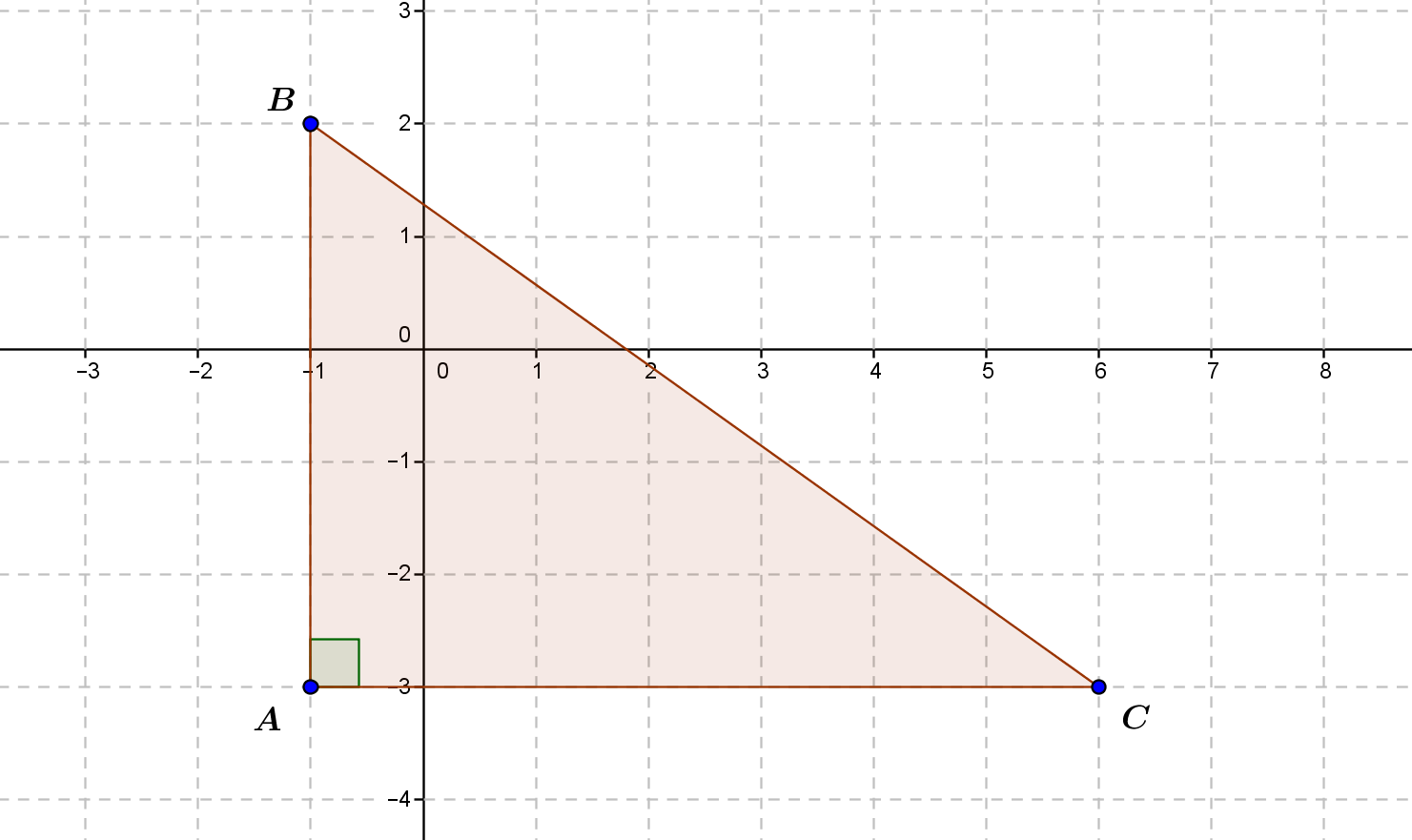
Dans le triangle \(ABC\) rectangle en \(A\), par le théorème de Pythagore l’aire du carré construit sur l’hypoténuse (soit le segment \([BC]\)) est la somme des aires des carrés construits sur les côtés \([AB]\) et \([BC]\). Ainsi, le carré \(BC^2\) de la longueur \(BC\) du côté \([BC]\) devrait être égale à la somme \(AB^2+AC^2\), soit ici \(5^2+7^2=25+49=74\), ou encore \(BC=\sqrt{74}\).

Or, lorsqu’on mesure, dans la tradition antique, des longueurs par des nombres rationnels, une telle racine carrée n’existe pas toujours. Par exemple, la diagonale d’un carré de longueur \(1\) doit être un nombre dont le carré vaut \(2\), et on peut démontrer que ce nombre n’existe pas, ce qui était connu dès l’Antiquité et constituait une véritable tragédie… grecque. On dit que « la diagonale du carré unité est incommensurable ».

Pour que l’approche analytique soit utile pour toute la géométrie euclidienne, il faut donc qu’elle puisse s’appliquer à tous ses objets, et notamment les angles et les cercles. C’est grâce à la construction des nombres réels que la possibilité de le faire a été fondée sur des bases solides.

R. Descartes

3. Représenter le plan euclidien grâce à l’ensemble des nombres réels

3.1. Les nombres réels au-delà des limitations traditionnelles

La construction des nombres réels, explorée dans notre article Qu’est-ce qu’un nombre réel ?, a joué un rôle crucial dans la résolution de questions sur l’existence de certaines grandeurs, introuvables dans l’ensemble des nombres rationnels. Cela concerne notamment les solutions d’équations numériques, ou diophantiennes, et l’existence de racines carrées pour tous les nombres positifs.`

Pour une compréhension approfondie, nous vous invitons à consulter dans notre encyclopédie MATHESIS::Essentiel un article clé : [La droite réelle] pour une approche axiomatique des nombres réels et une exploration de l’existence des racines $n$-ièmes.

En particulier, en ce qui concerne la traduction dans ou par le calcul des propriétés de la géométrie euclidienne, les limites de l’approche cartésienne par coordonnées associées au calcul des longueurs, sont levées si l’on veut bien concevoir que les coordonnées d’un point du plan sont des nombres réels et pas des nombres rationnels. Autrement dit, la tragédie « pythagoricienne » de l’incommensurabilité de la diagonale du carré unité a trouvé une fin heureuse à l’époque moderne, mais la civilisation grecque n’en a pas profité (pour ce que nous en savons).

3.2. \(\mathbb R^2\) comme représentation ensembliste du plan euclidien

Retrouvez l’article en vidéo sur MATHESIS, la chaîne YouTube :

Pour aller plus loin