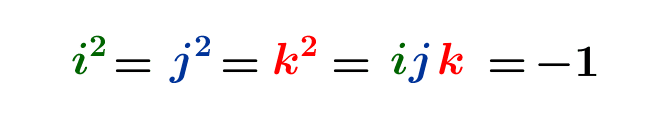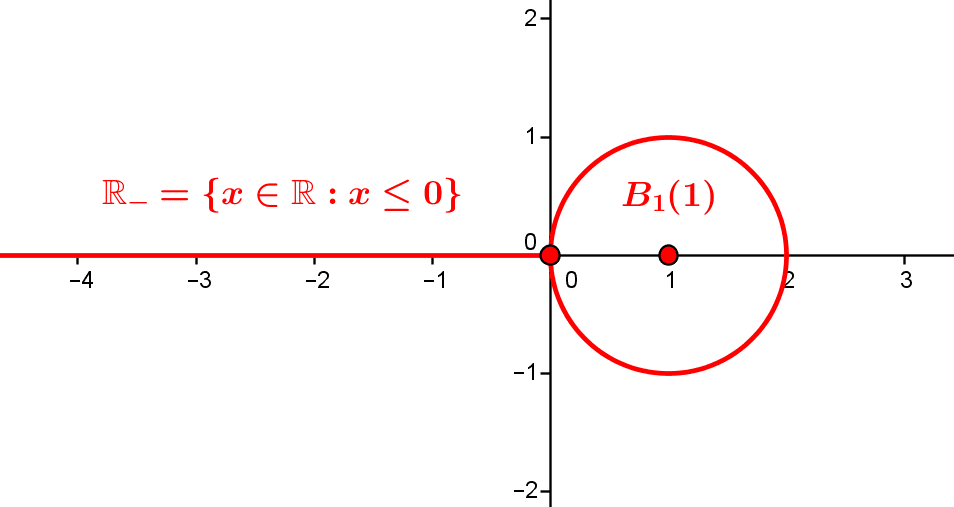la Règle et le Compas
Explorez l’Infini
Une approche philosophique
de la science mathématique
Anneaux, homomorphismes et quotients
Nous étudions la structure mathématique naturelle d'anneau, dont l'ensemble $\mathbb Z$ des entiers relatifs est le prototype, et qui permet d'interpréter de nombreux concepts de la théorie des nombres et de la géométrie, à travers notamment les notions...
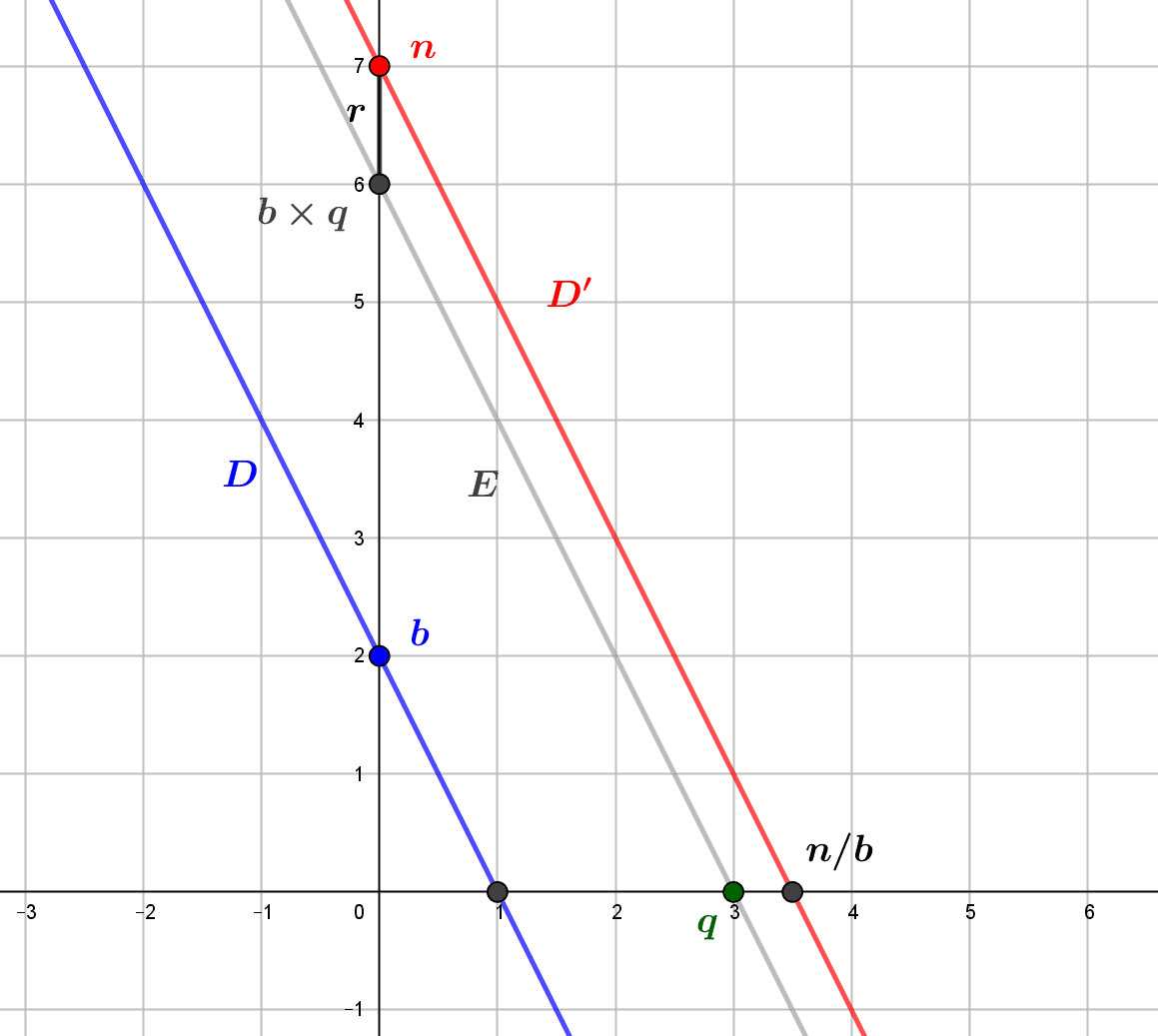
Division euclidienne et arithmétique modulaire
La division des entiers naturels ne donne pas toujours un résultat entier, et la division euclidienne donne une meilleure approximation de ce résultat, sous la forme d'un quotient et d'un reste. On peut définir une addition et une multiplication "modulaires" sur les...
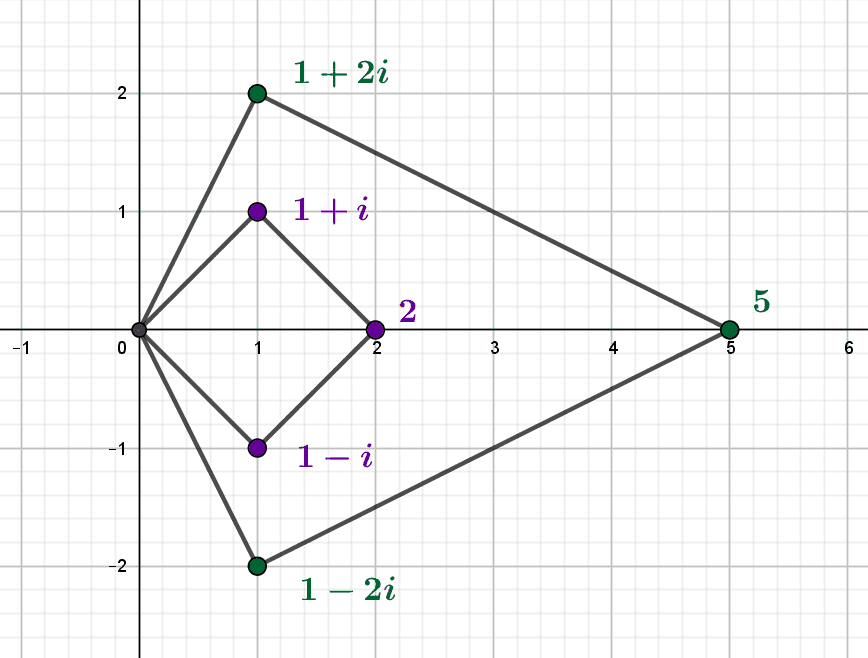
La ramification imaginaire des nombres premiers
Nous savons que les nombres premiers ne demeurent premiers dans l'anneau \(\mathbb Z[i]\) des entiers de Gauss que lorsqu'ils sont sommes de deux carrés. En considérant leurs congruences modulo \(4\), il est possible d'en dire plus : on peut les classer en trois types...
Un algorithme de calcul des racines carrées
En utilisant la somme des premiers nombres impairs dans l'ordre, on peut définir un algorithme simple de calcul des racines carrées des nombres entiers avec une précision décimale arbitraire. 1.Calcul de la somme des \(n\) premiers entiers naturels impairs Il est,...
Plus de réels que de rationnels : un argument diagonal par les bases de numération
Dans cet article, nous abordons la question du "comptage" des nombres réels, autrement dit de la détermination du cardinal de l'ensemble \(\mathbb R\). Celui-ci est strictement supérieur au cardinal de l'ensemble des nombres rationnels, ce que nous expliquons de deux...
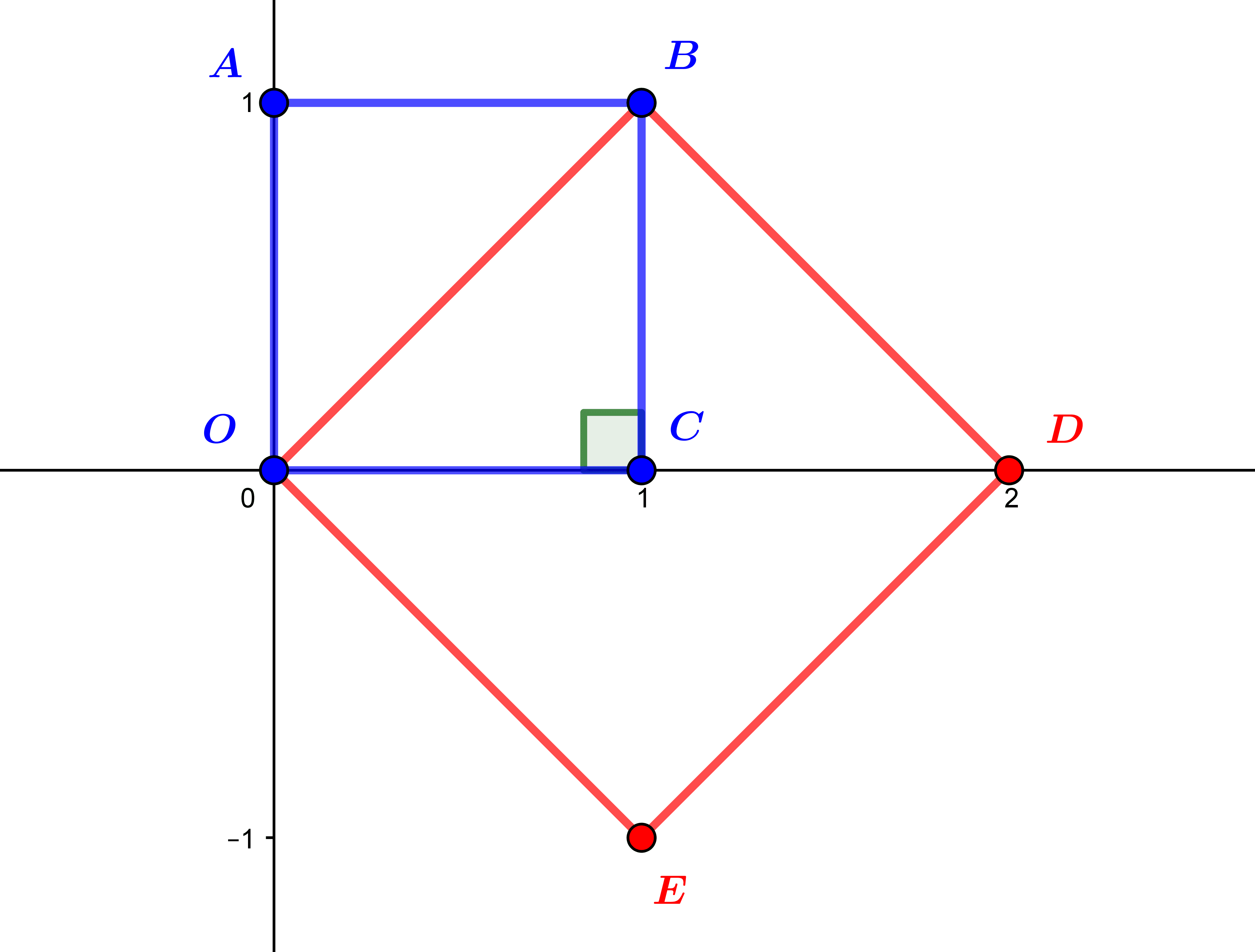
L’irrationalité de √2 : une tragédie pythagoricienne
Les tragédies grecques existaient aussi chez les mathématiciens de l'Antiquité. La découverte de la racine carrée du nombre 2 est le sujet de l'une d'entre elles, qui a trouvé une fin heureuse à l'époque moderne. 1.Un disciple de Pythagore "mesure" la diagonale du...
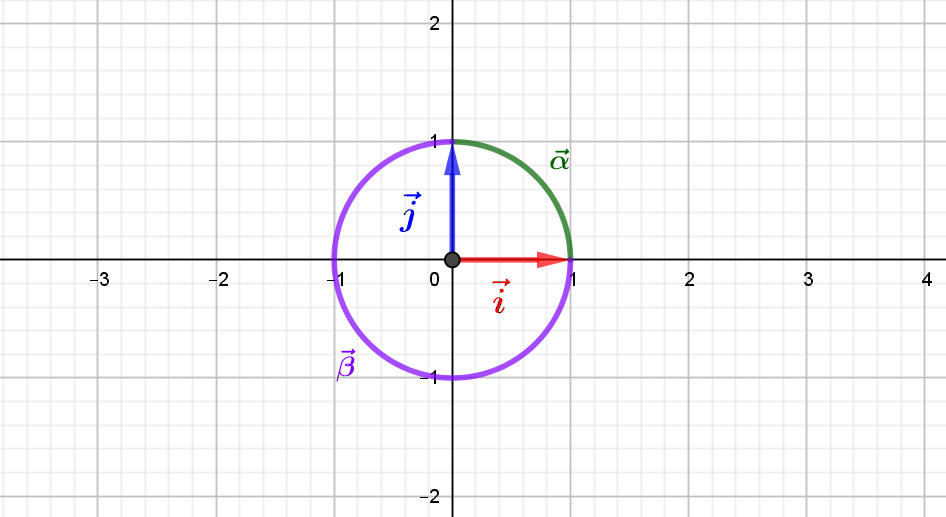
L’orientation du plan euclidien : bases et angles
L'intuition visuelle à travers laquelle nous représentons le plan euclidien suggère que nous puissions l'orienter selon un sens de rotation. Cette intuition reflète une définition mathématique rigoureuse de l'orientation du plan, qui consiste à choisir une base, et...
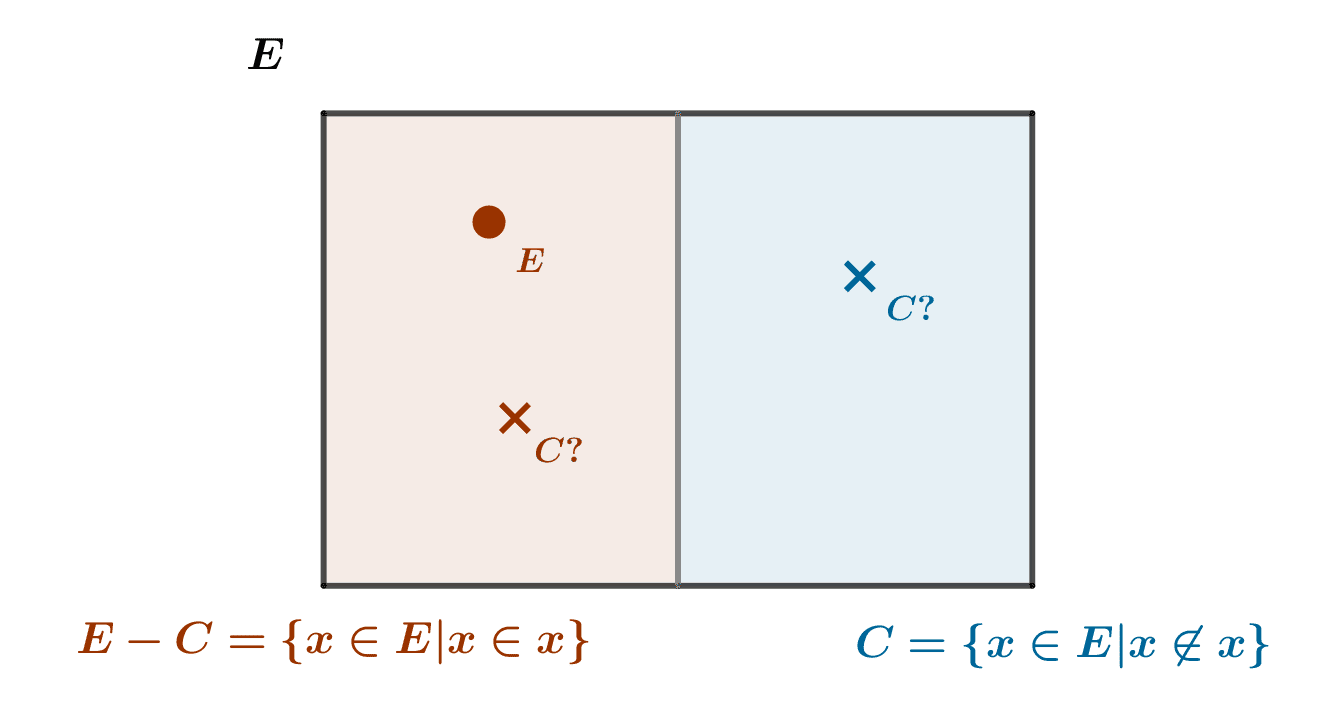
Le paradoxe de Russell et la théorie des classes
Le paradoxe ou antinomie de Russell est un paradoxe très simple de la théorie naïve des ensembles, qui surgit lorsqu'on cherche à définir un "ensemble de tous les ensembles". Sa résolution repose sur l'introduction de la notion de classe et la distinction des...
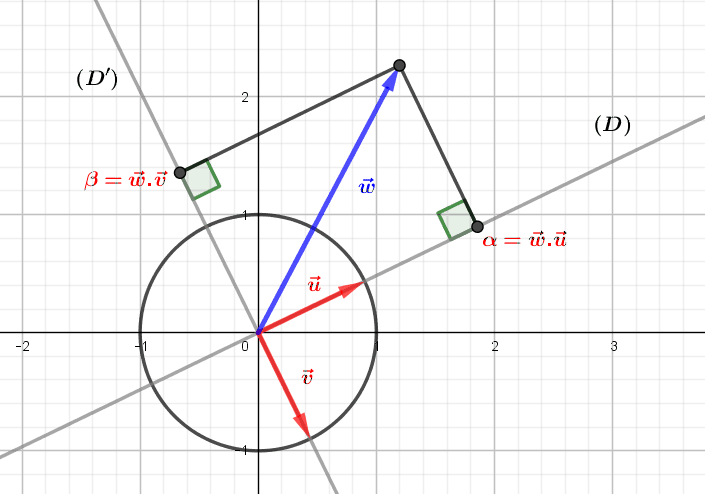
Les transformations linéaires du plan : déterminant, bases et inversion
Les transformations linéaires du plan euclidien sont les applications linéaires inversibles, c'est-à-dire de déterminant non nul. Elles permettent de passer d'une base du plan à une autre, et les transformations orthogonales, c'est-à-dire les isométries vectorielles,...
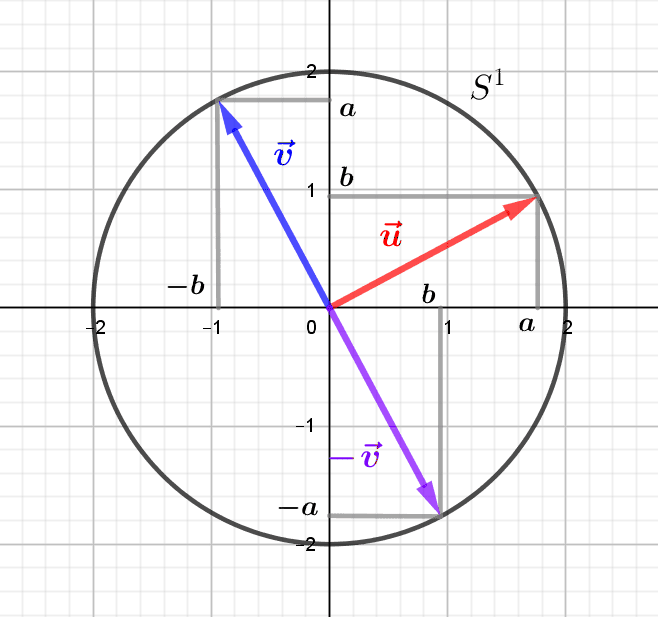
Les bases du plan euclidien : vecteurs et coordonnées
La représentation du plan euclidien par le produit cartésien \(\mathbb R^2\) permet de décomposer tout vecteur du plan en deux coordonnées, son abscisse et son ordonnée. Cette décomposition est liée à un "système de représentation" particulier et naturel, qu'on...
L’espace euclidien : points, vecteurs et produit scalaire
La méthode analytique de Descartes, qui permet de représenter le plan euclidien comme le produit cartésien \(\mathbb R^2\) grâce à la théorie des nombres réels, permet également de représenter l'espace euclidien comme le produit cartésien \(\mathbb R^3=\mathbb...
Les quaternions de Hamilton : un espace-temps algébrique
La multiplication complexe se prolonge naturellement à une multiplication en quatre dimensions, qui définit sur l'espace \(\mathbb R^4\) la structure de l'algèbre \(\mathbb H\) des quaternions de Hamilton. Cette multiplication s'interprète géométriquement à partir du...
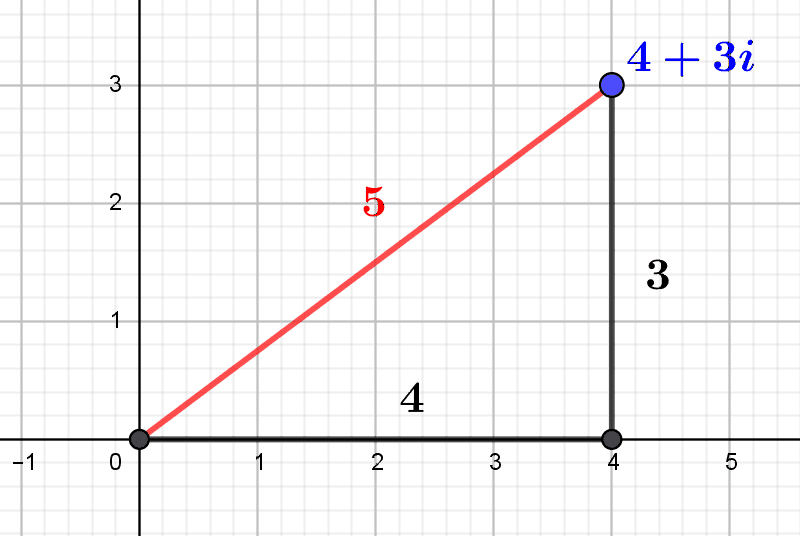
Les entiers de Gauss : une arithmétique imaginaire
Les entiers de Gauss sont les nombres complexes à coordonnées entières. Grâce à leur norme, sorte de mesure entière de leur taille, on peut décrire certaines de leurs propriétés arithmétiques. En particulier, on peut effectuer des divisions euclidiennes et déterminer...
Une définition analytique du nombre π
Introduction Lorsque nous avons introduit l'exponentielle circulaire, les fonctions trigonométriques cosinus et sinus ont été définies comme sa partie réelle et sa partie imaginaire. Nous en avons alors tiré les expressions analytiques : \(\cos x=\sum_{n=0}^{+\infty}...
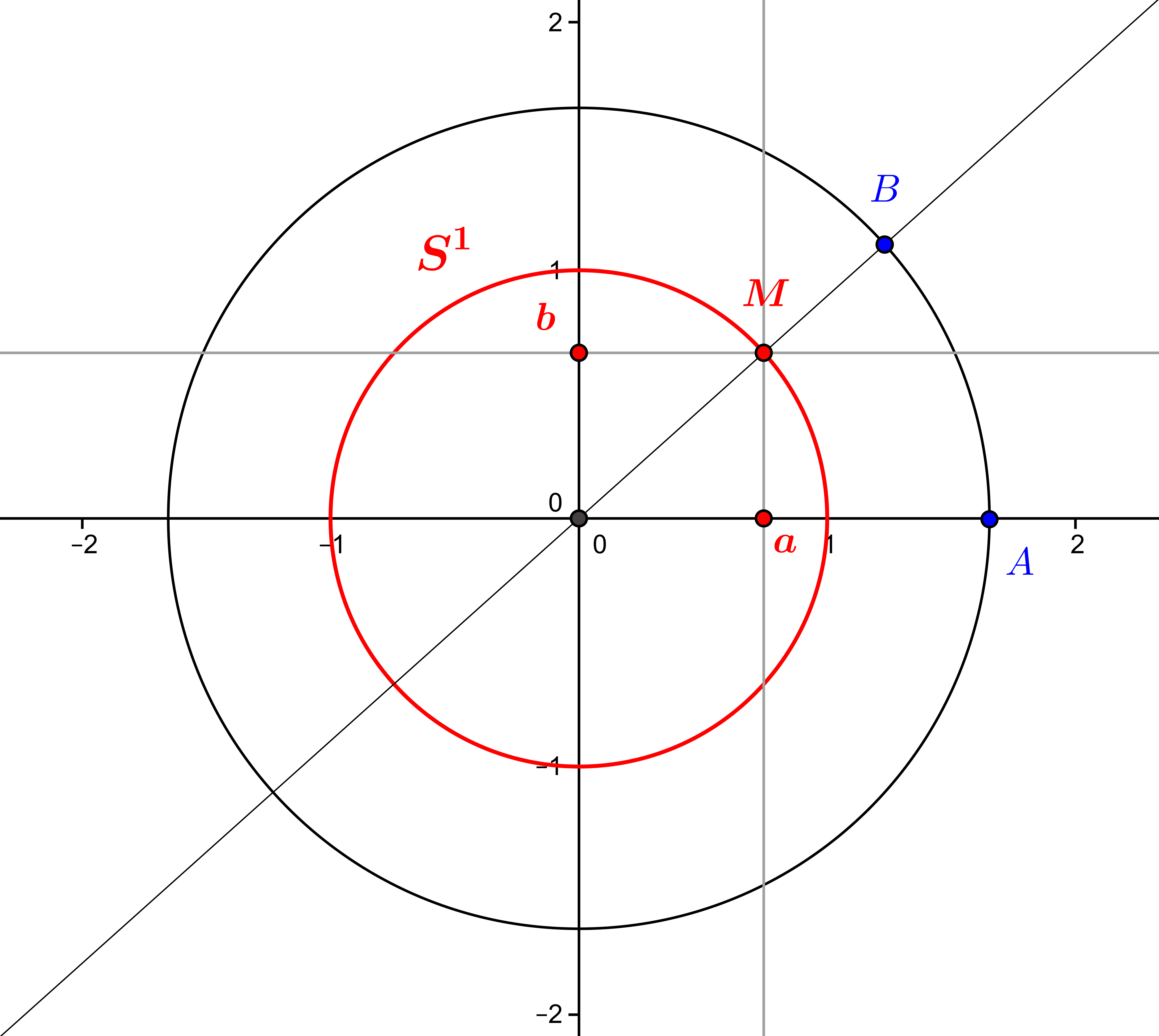
La mesure des angles de vecteurs : où l’analyse rencontre l’algèbre
Introduction Dans Angles de vecteurs : intuition géométrique et définition algébrique, nous avons défini et décrit le groupe des angles de vecteurs du plan euclidien de manière algébrique, en utilisant une relation d'équivalence sur les vecteurs unitaires. De...
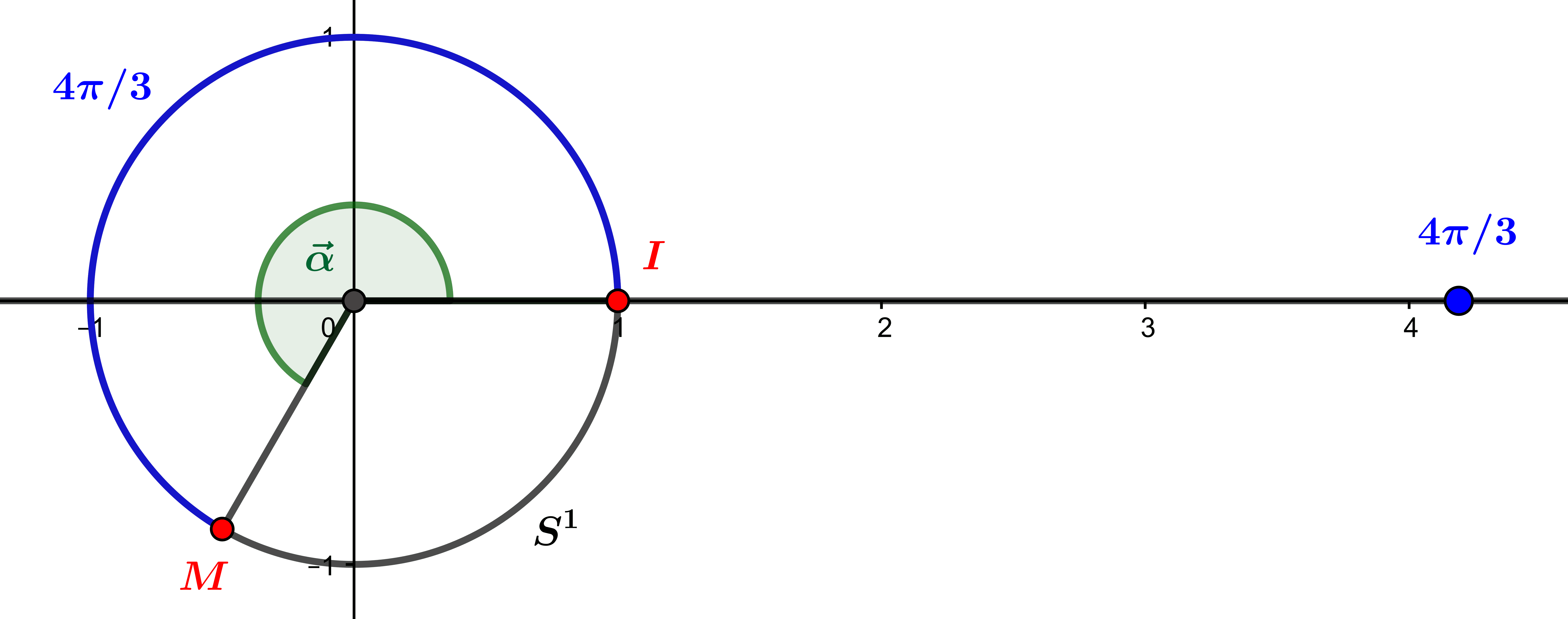
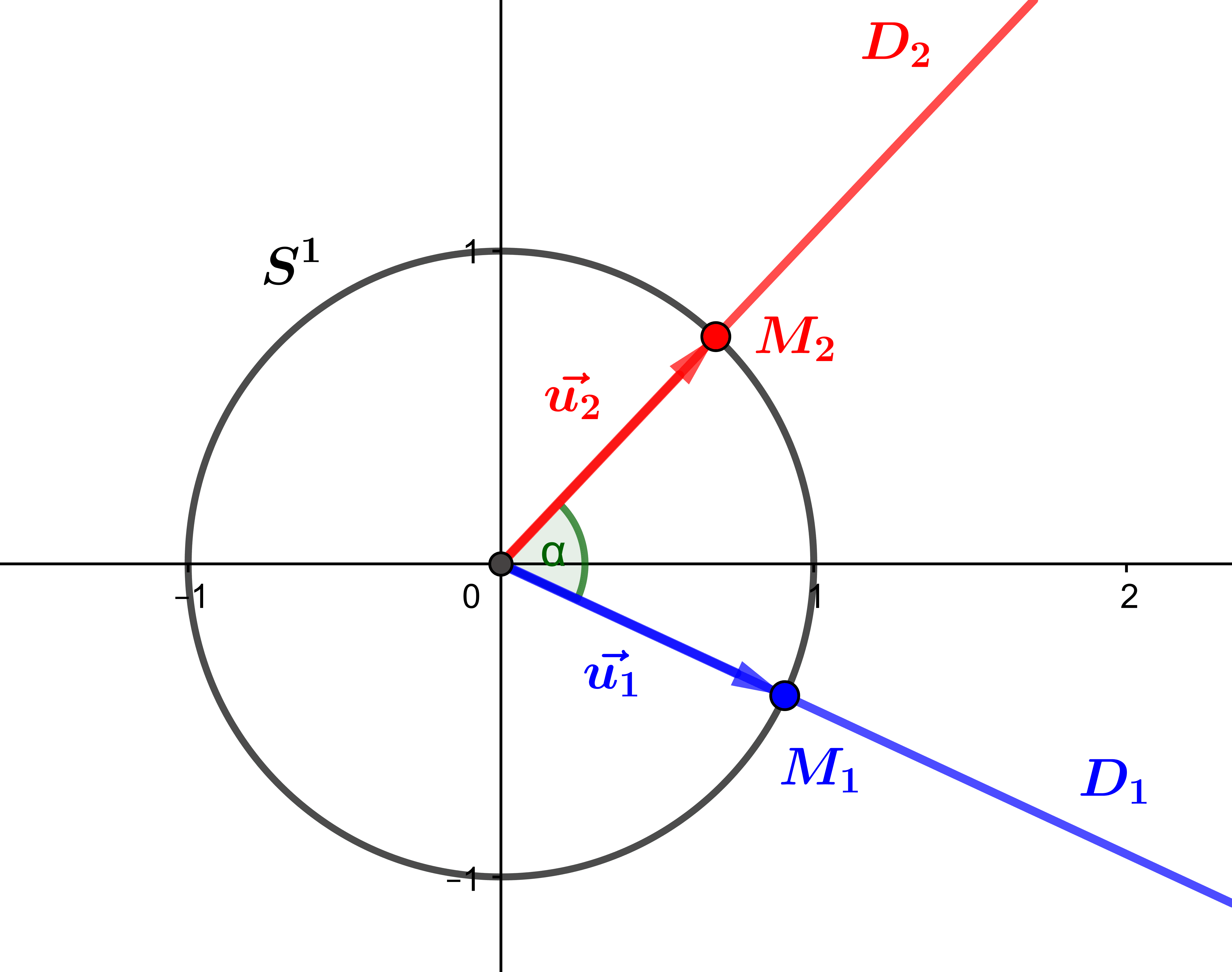
Angles de vecteurs : intuition géométrique et définition algébrique
Les angles de vecteurs sont les angles orientés habituels de la géométrie euclidienne plane. Grâce aux ressources de la théorie naïve des ensembles, on les définit de manière purement algébrique grâce à une relation d'équivalence et aux rotations vectorielles du plan....
Rotations vectorielles du plan : l’approche « analytique »
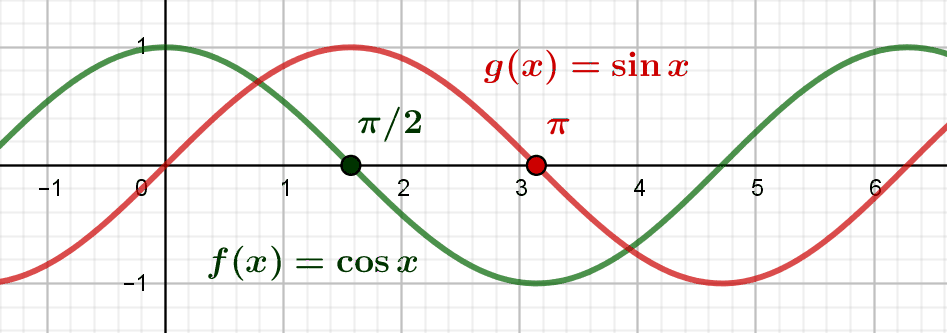
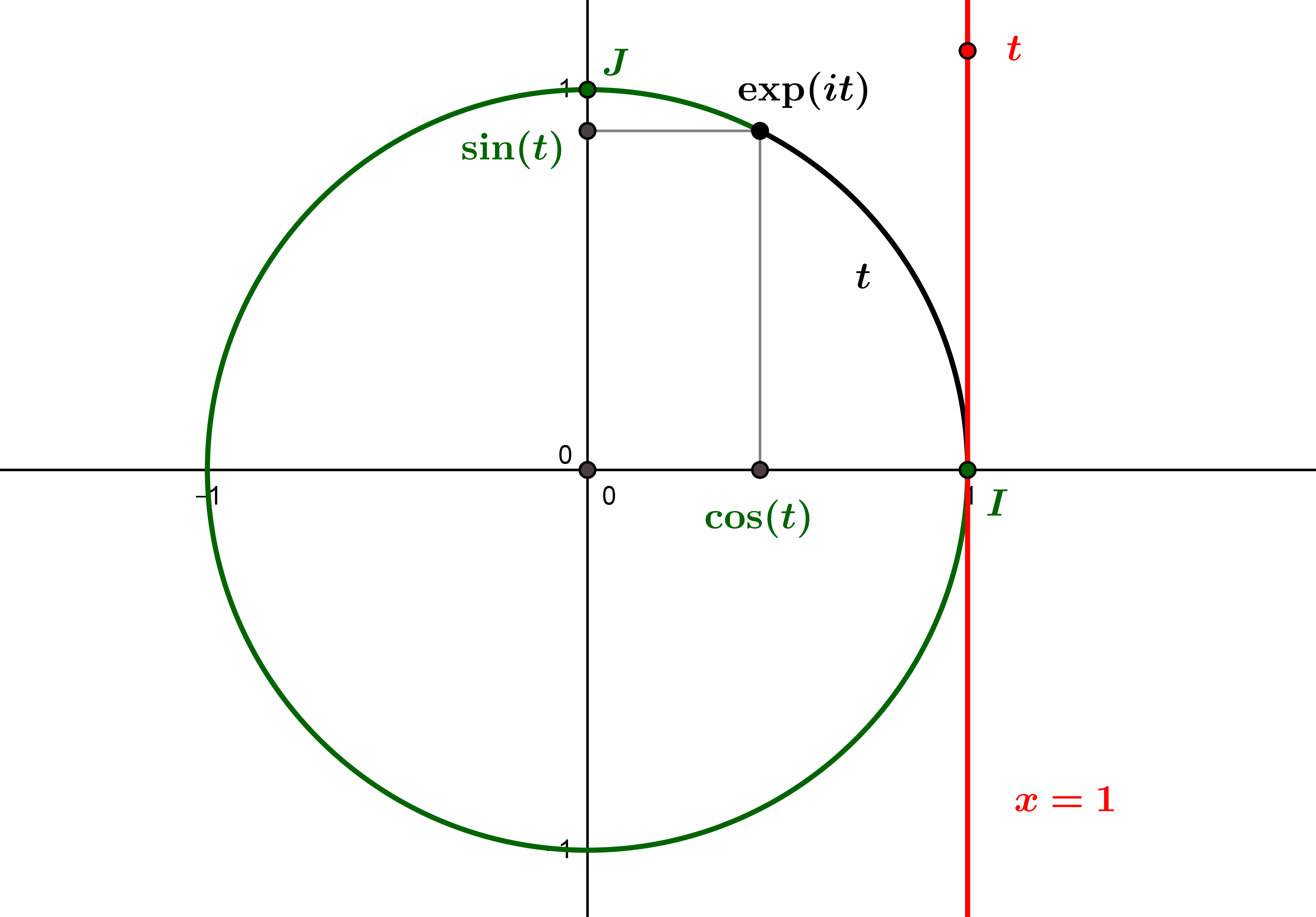
L’exponentielle circulaire et les fonctions trigonométriques
A partir de la fonction exponentielle complexe, on peut définir une fonction "exponentielle circulaire", qui "enroule" la droite réelle sur le cercle trigonométrique, et permet de définir rigoureusement les fonctions trigonométriques cosinus et sinus, qui s'étendent à...
Fonctions analytiques et exponentielle complexe
Certaines fonctions indéfiniment dérivables peuvent être décrites "autour de chaque point" comme la somme d'une série dite "entière". Il s'agit des fonctions analytiques, réelles ou complexes, dont l'exemple typique est celui de la fonction exponentielle, qu'on peut...
Une infinité de nombres premiers
Les nombres entiers naturels premiers sont sont ceux qui n'ont pas d'autres diviseurs que 1 et eux-mêmes. Ils existent en nombre infini par le théorème d'Euclide, qui n'est pas difficile à démontrer. 1.Les nombres premiers Diviseurs et nombres premiers Un nombre...