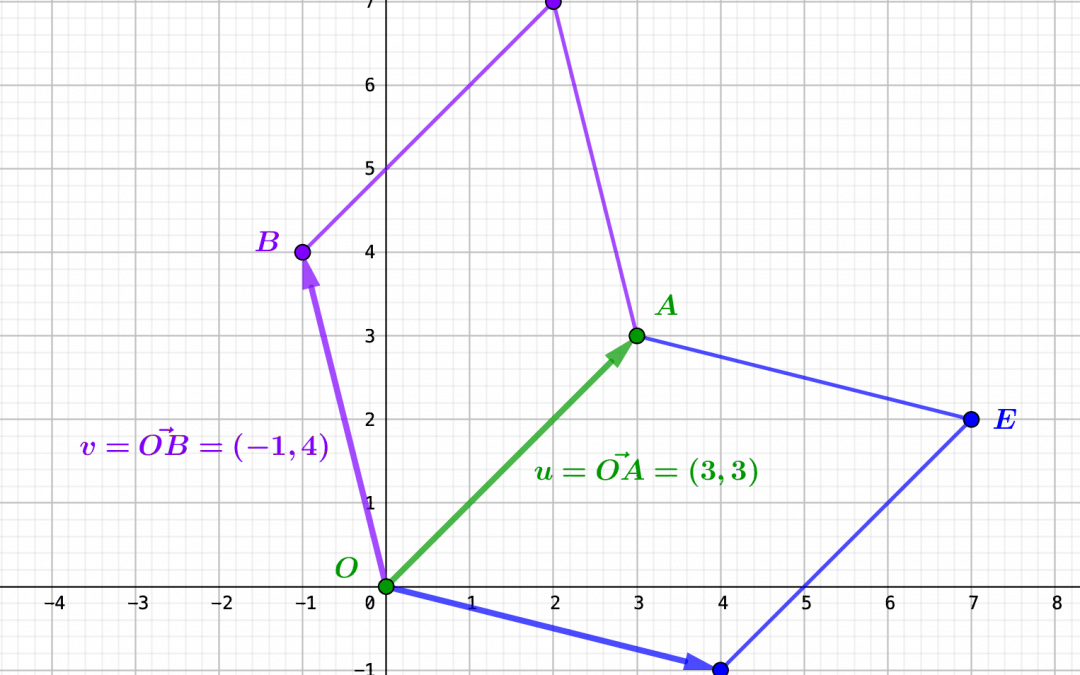
par Jean Barbet | Nov 29, 2023 | Algèbre, Géométrie, Trigonométrie
Le produit scalaire et le déterminant sont des concepts clés de l’algèbre linéaire dans le plan euclidien, offrant une compréhension profonde des relations entre deux vecteurs $u$ et $v$. Lorsque ces vecteurs sont unitaires, leur produit scalaire et déterminant...
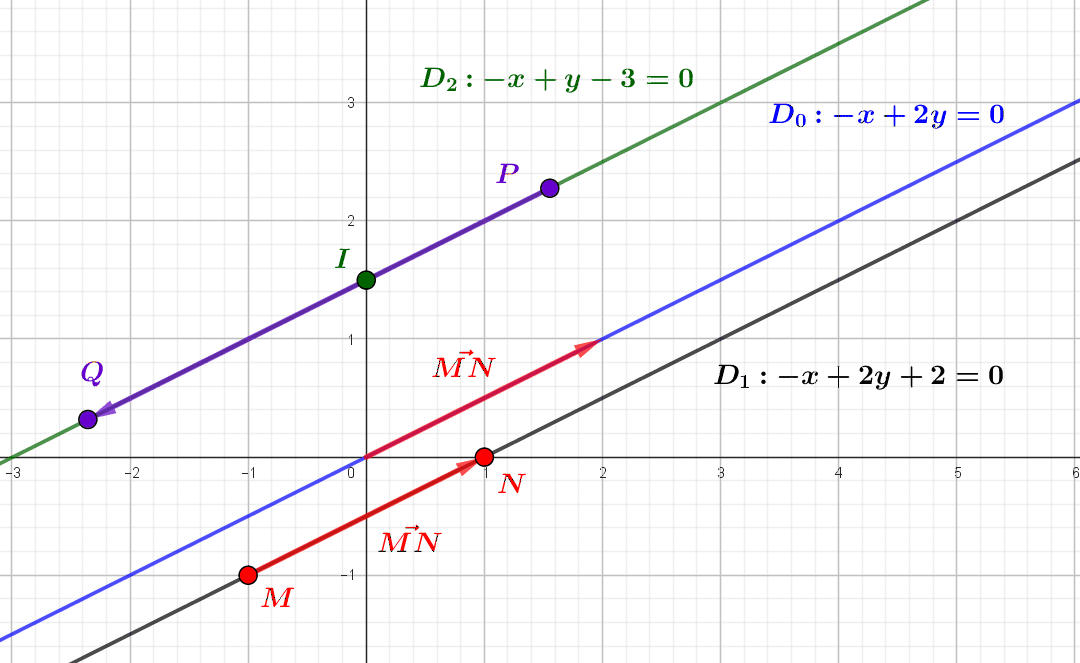
par Jean Barbet | Avr 21, 2023 | Algèbre, Géométrie
L’approche analytique de la géométrie plane, que nous devons à Descartes, permet de donner une description purement algébrique des droites du plan comme ensembles de solutions d’équations d’un seul type. Ces équations dites cartésiennes contiennent...
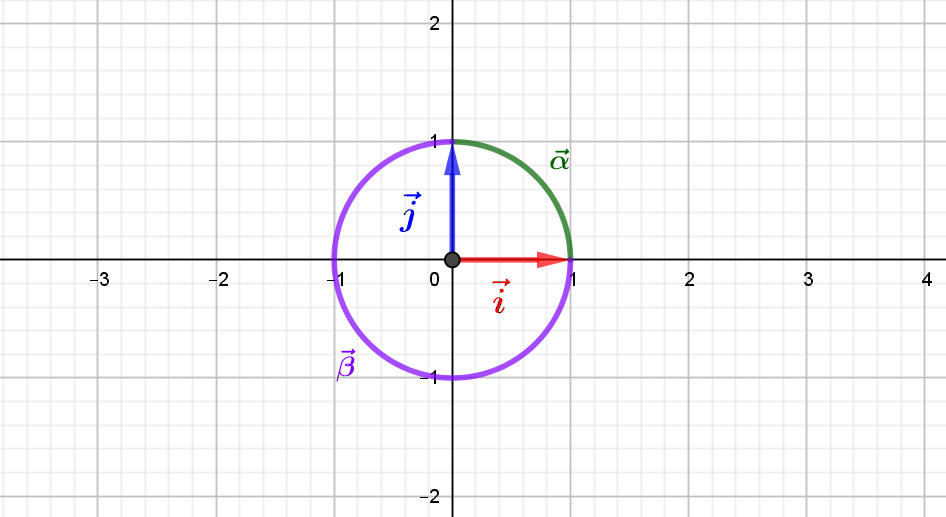
par Jean Barbet | Juin 21, 2021 | Algèbre, Géométrie
L’intuition visuelle à travers laquelle nous représentons le plan euclidien suggère que nous puissions l’orienter selon un sens de rotation. Cette intuition reflète une définition mathématique rigoureuse de l’orientation du plan, qui consiste à...
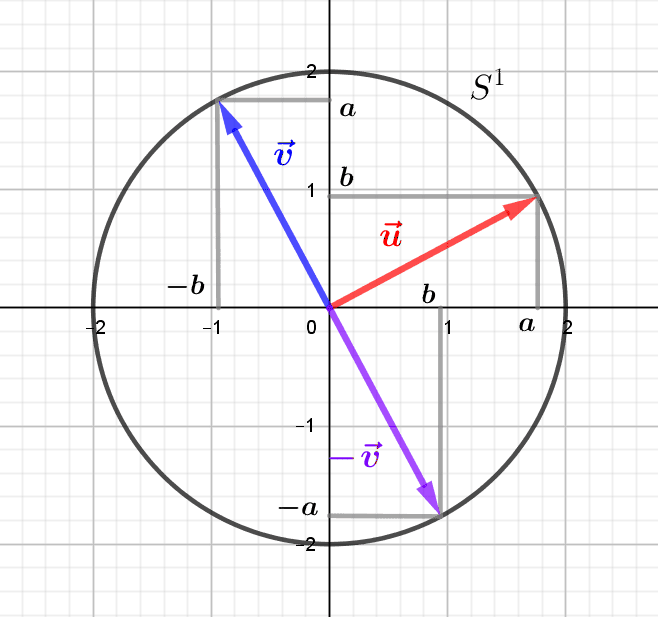
par Jean Barbet | Mai 22, 2021 | Algèbre, Géométrie
Les transformations linéaires du plan euclidien sont les applications linéaires inversibles, c’est-à-dire de déterminant non nul. Elles permettent de passer d’une base du plan à une autre, et les transformations orthogonales, c’est-à-dire les...
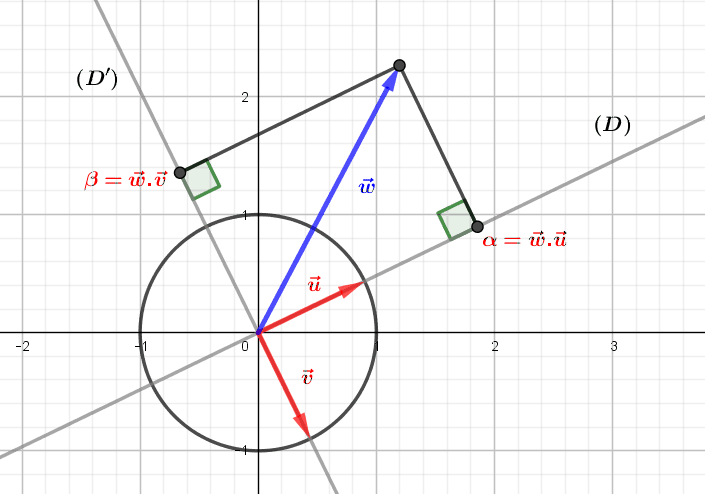
par Jean Barbet | Mai 7, 2021 | Algèbre, Géométrie
La représentation du plan euclidien par le produit cartésien \(\mathbb R^2\) permet de décomposer tout vecteur du plan en deux coordonnées, son abscisse et son ordonnée. Cette décomposition est liée à un « système de représentation » particulier et naturel,...






