par Jean Barbet | Juin 29, 2024 | Analyse, Cinématique, Géométrie
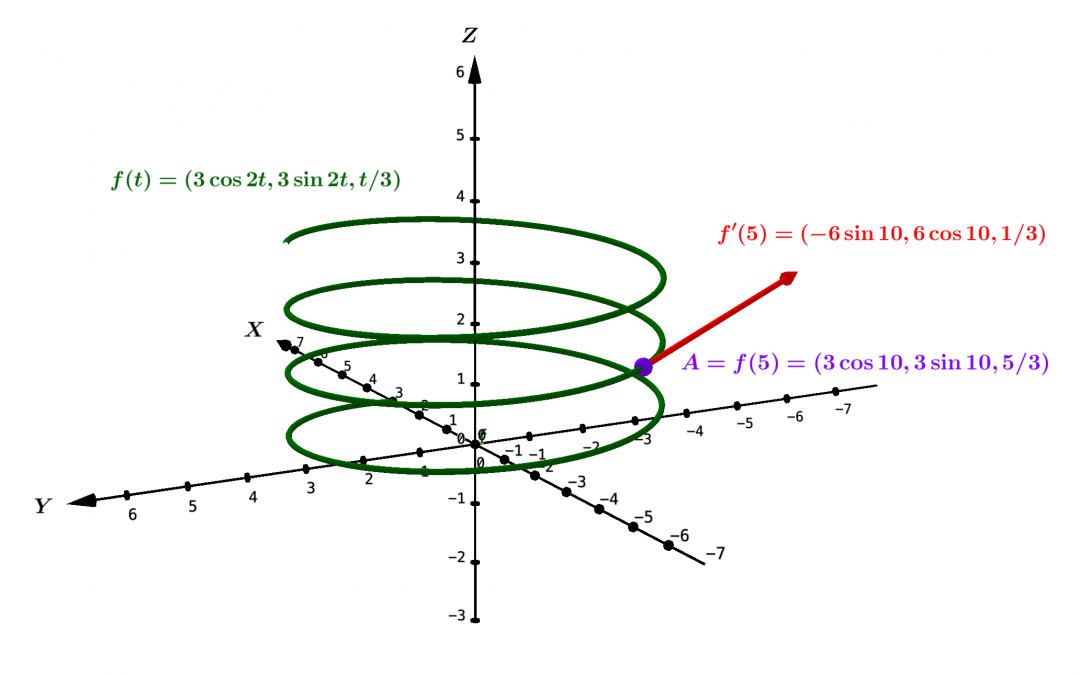
Dans la géométrie différentielle, l’analyse réelle et la géométrie euclidienne convergent vers une description infinitésimale des objets géométriques naturels, qui permet d’en étudier avec précision certains paramètres standard. Nous commençons avec...
par Jean Barbet | Juin 18, 2024 | Analyse, Fonctions
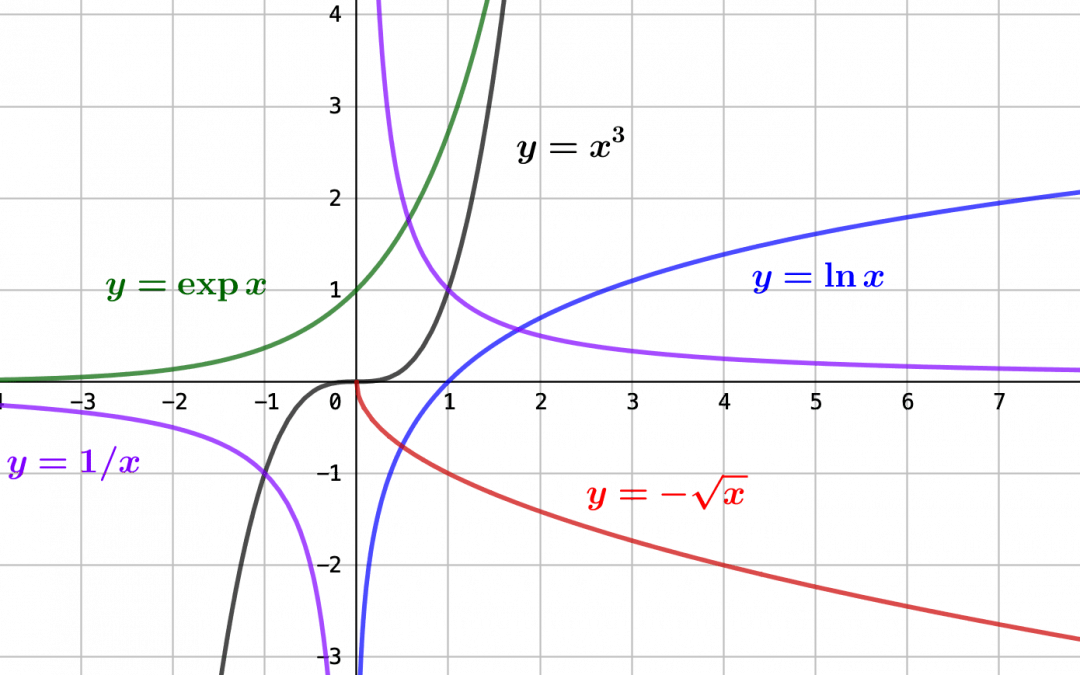
Les propriétés de l’analyse des fonctions d’une variable réelle sont celles qui sont associées à la structure de la droite réelle. L’ordre entre nombres réels, représentation de l’ordre entre les grandeurs naturelles, est l’élément...

par Jean Barbet | Juin 5, 2024 | Ensembles, Logique
En nous appuyant sur les notions d’objet et de classe issues de la logique naturelle, nous avons redéfini le concept d’ensemble de manière intuitive, établissant ainsi une théorie naturelle des ensembles sans recourir à la logique formelle. Cette approche...

par Jean Barbet | Mai 5, 2024 | Ensembles, Logique
La révolution des mathématiques est celle de la théorie des ensembles, qui répond à la fois au problème d’un langage conceptuel universel et rigoureux, et à celui d’un fondement unique pour toutes les disciplines mathématiques. Si la théorie des ensembles...
par Jean Barbet | Avr 30, 2024 | Analyse, Ensembles, Nombres
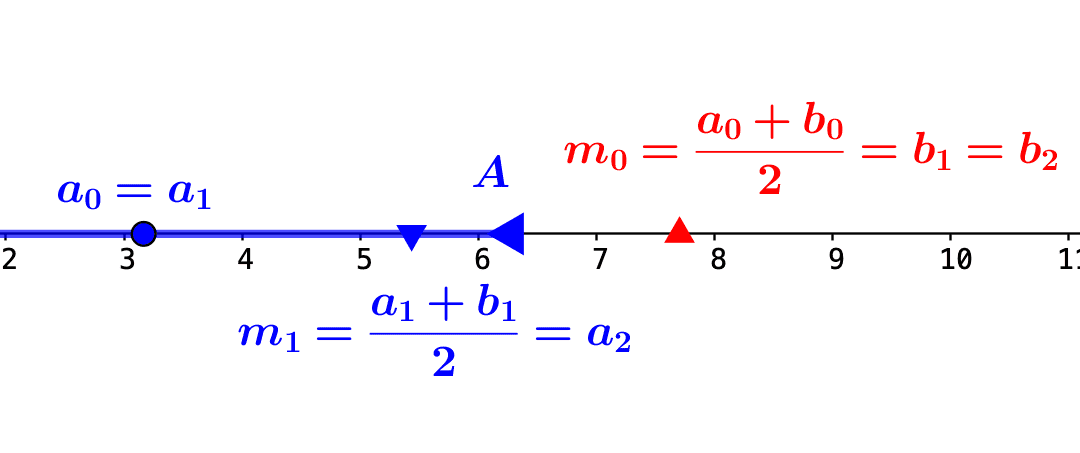
L’ensemble des nombres réels, quelle que soit la manière dont il est présenté, défini ou construit, n’est pas une multiplicité « amorphe », mais il vient avec une « structure » naturelle, héritée en dernière analyse de la structure arithmétique de...






