
par Jean Barbet | Juin 6, 2023 | Algèbre, Nombres
Les corps finis traduisent sur le plan structurel certaines propriétés arithmétiques et servent de « corps de restes » en théorie des nombres. Par analogie avec les corps $\mathbb R$ des nombres réels et $\mathbb C$ des nombres complexes, le nombre $-1$ peut y...

par Jean Barbet | Oct 1, 2022 | Algèbre, Nombres
L’anneau des entiers de Gauss \(\mathbb Z[i]\) possède des propriétés remarquables, analogues à celles de l’ensemble \(\mathbb Z\) des nombres entiers relatifs. Il existe toute une famille de tels anneaux, possédant des propriétés similaires, et définis...

par Jean Barbet | Juil 28, 2022 | Algèbre, Nombres
Deux nombres entiers sont dits premiers entre eux si ils n’ont pas de facteur premier en commun : il sont donc premiers « l’un par rapport à l’autre ». Le nombre des restes modulo un entier naturel non nul $n$ qui sont premiers avec $n$ est ce...
par Jean Barbet | Juin 28, 2022 | Algèbre, Nombres
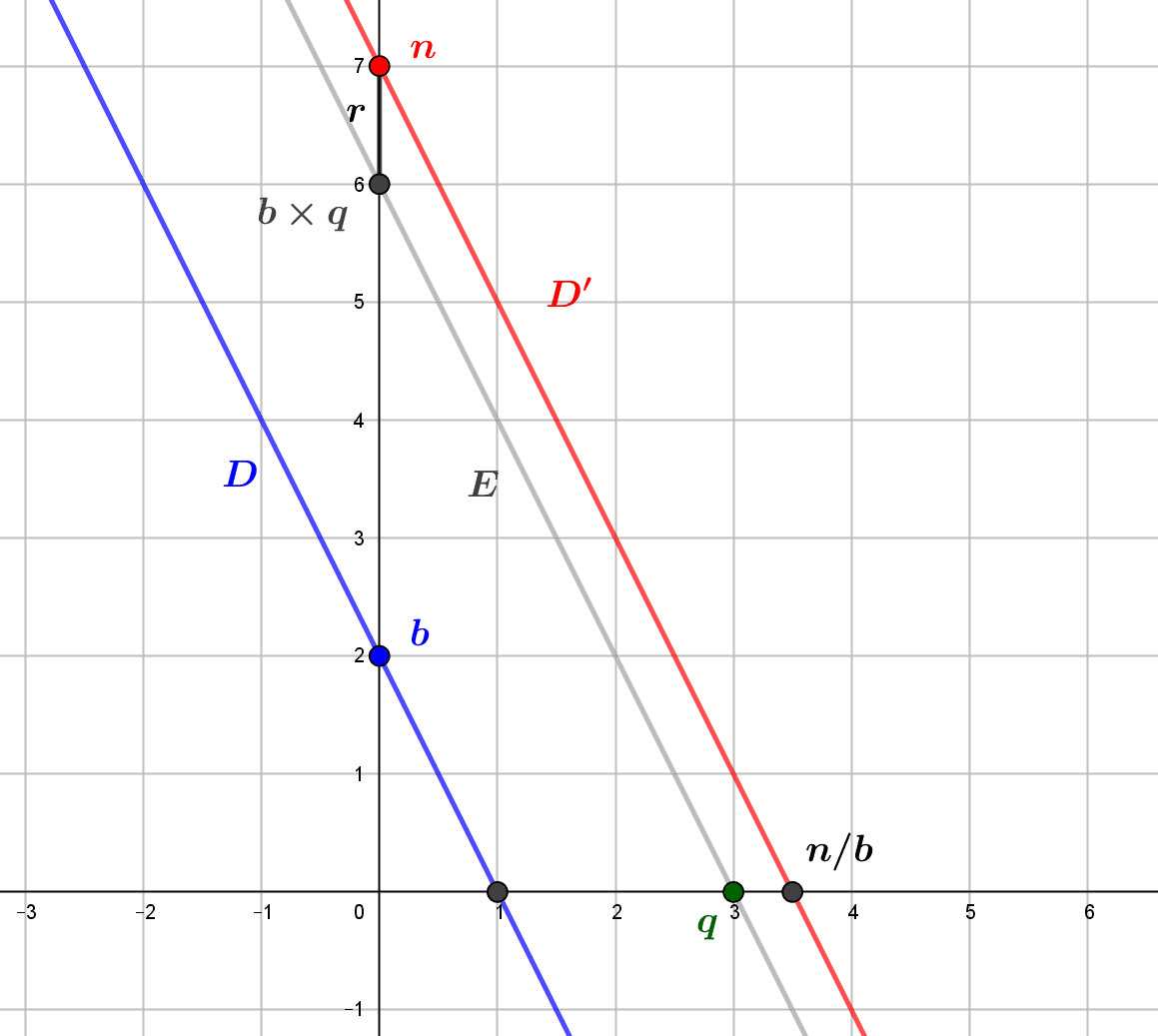
La division des entiers naturels ne donne pas toujours un résultat entier, et la division euclidienne donne une meilleure approximation de ce résultat, sous la forme d’un quotient et d’un reste. On peut définir une addition et une multiplication...
par Jean Barbet | Mai 28, 2022 | Algèbre, Nombres
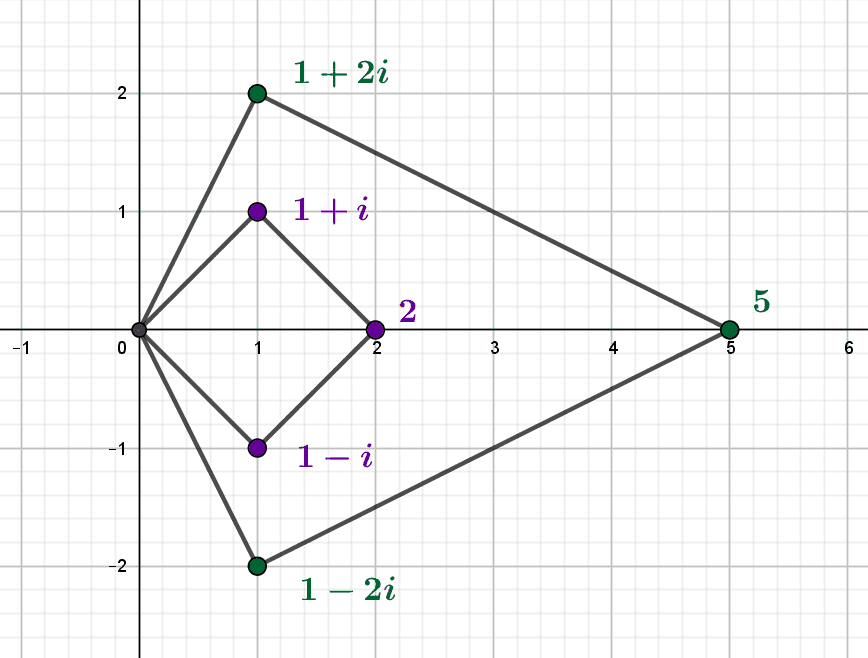
Nous savons que les nombres premiers ne demeurent premiers dans l’anneau \(\mathbb Z[i]\) des entiers de Gauss que lorsqu’ils sont sommes de deux carrés. En considérant leurs congruences modulo \(4\), il est possible d’en dire plus : on peut les...

par Jean Barbet | Jan 14, 2022 | Nombres
En utilisant la somme des premiers nombres impairs dans l’ordre, on peut définir un algorithme simple de calcul des racines carrées des nombres entiers avec une précision décimale arbitraire. 1.Calcul de la somme des \(n\) premiers entiers naturels impairs Il...







