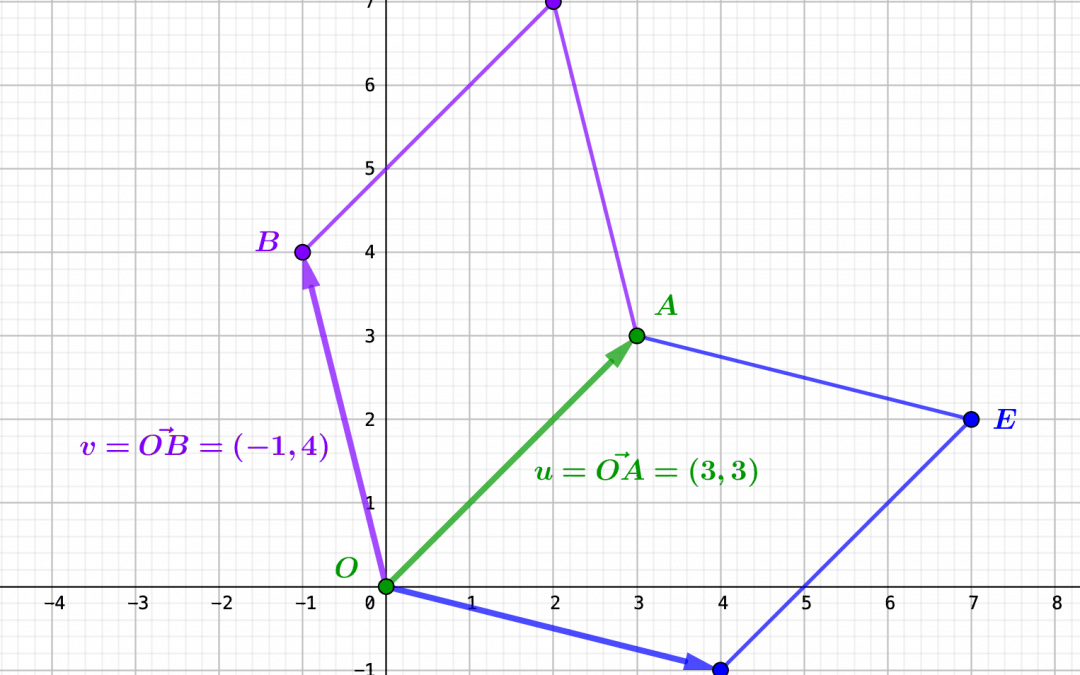
par Jean Barbet | Jan 19, 2024 | Algèbre, Géométrie, Nombres
Le plan euclidien acquiert une orientation naturelle par le choix d’une base, que l’on peut qualifier de directe ou d’indirecte. Cette orientation se manifeste à travers le signe du déterminant de la base, correspondant à l’aire algébrique du...
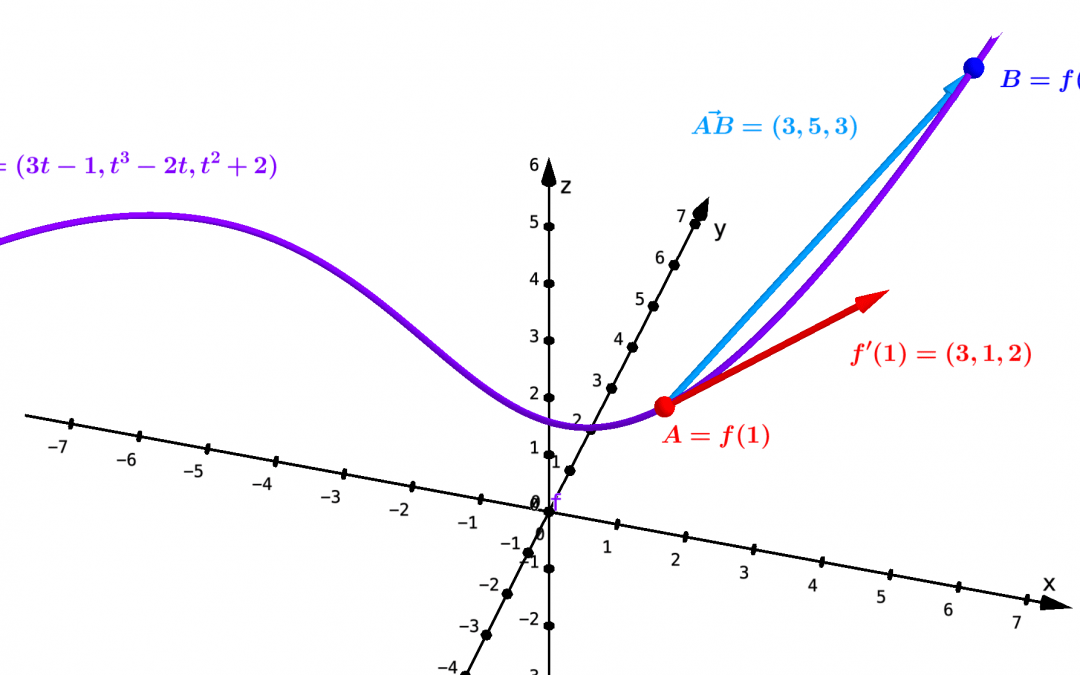
par Jean Barbet | Déc 22, 2023 | Cinématique, Géométrie
L’approche mathématique de la physique s’initie souvent par la description du mouvement. Cette démarche s’appuie sur la conceptualisation du mouvement en tant que variation de position en fonction du temps, ce qui conduit à sa modélisation comme une...
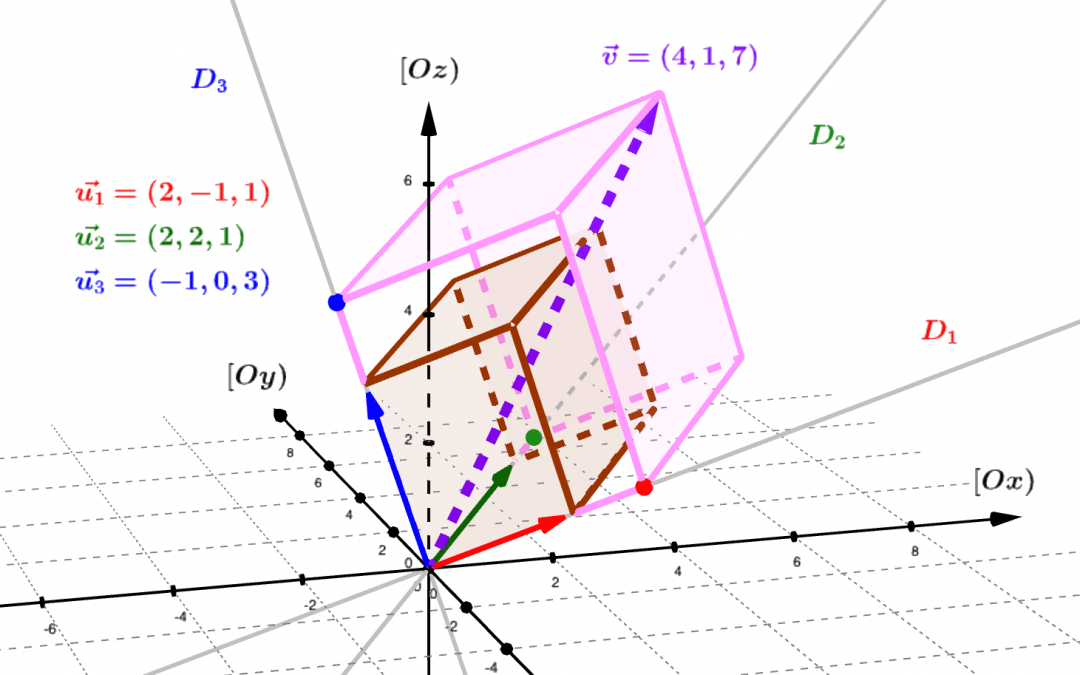
par Jean Barbet | Nov 29, 2023 | Algèbre, Géométrie, Trigonométrie
Le produit scalaire et le déterminant sont des concepts clés de l’algèbre linéaire dans le plan euclidien, offrant une compréhension profonde des relations entre deux vecteurs $u$ et $v$. Lorsque ces vecteurs sont unitaires, leur produit scalaire et déterminant...
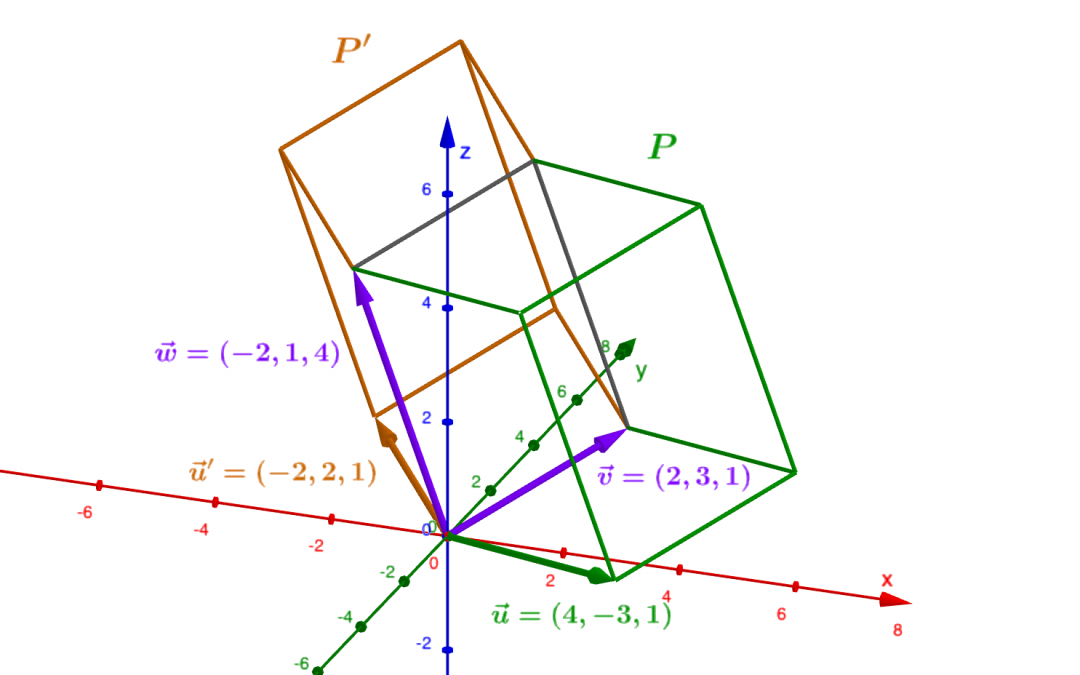
par Jean Barbet | Juil 3, 2023 | Algèbre, Géométrie
Comme dans le plan euclidien $\mathbb R^2$ , il existe dans l’espace euclidien $\mathbb R^3$ une infinité de bases ou « systèmes de représentation » des vecteurs : l’espace étant intuitivement de dimension 3, ces bases sont toujours formées de 3 vecteurs...
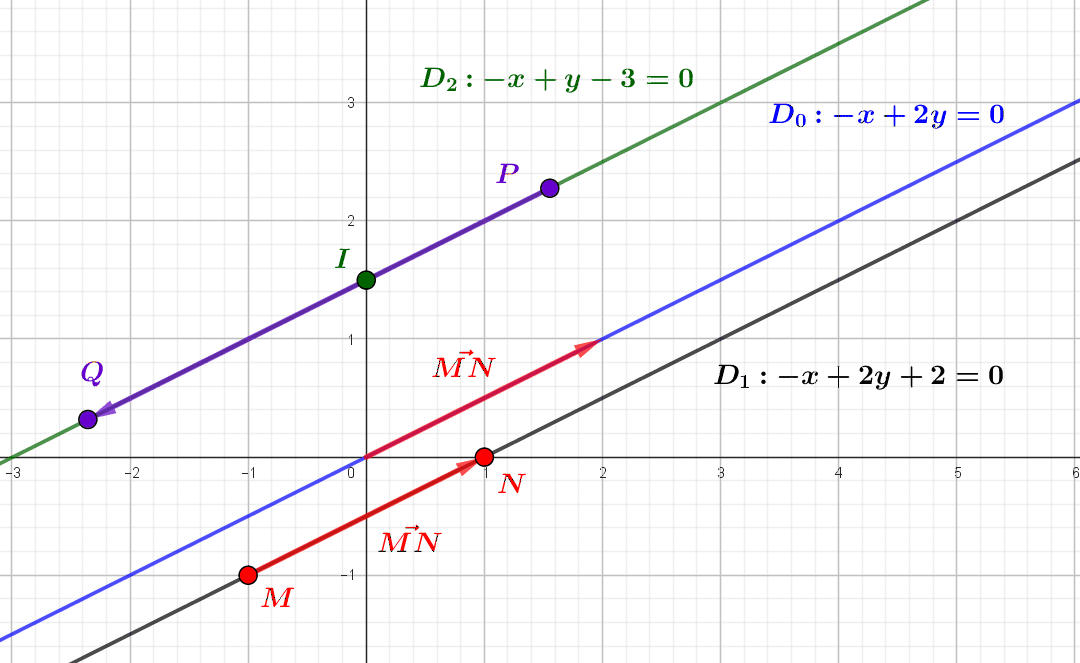
par Jean Barbet | Avr 21, 2023 | Algèbre, Géométrie
L’approche analytique de la géométrie plane, que nous devons à Descartes, permet de donner une description purement algébrique des droites du plan comme ensembles de solutions d’équations d’un seul type. Ces équations dites cartésiennes contiennent...






