par Jean Barbet | Jan 19, 2024 | Algèbre, Géométrie, Nombres
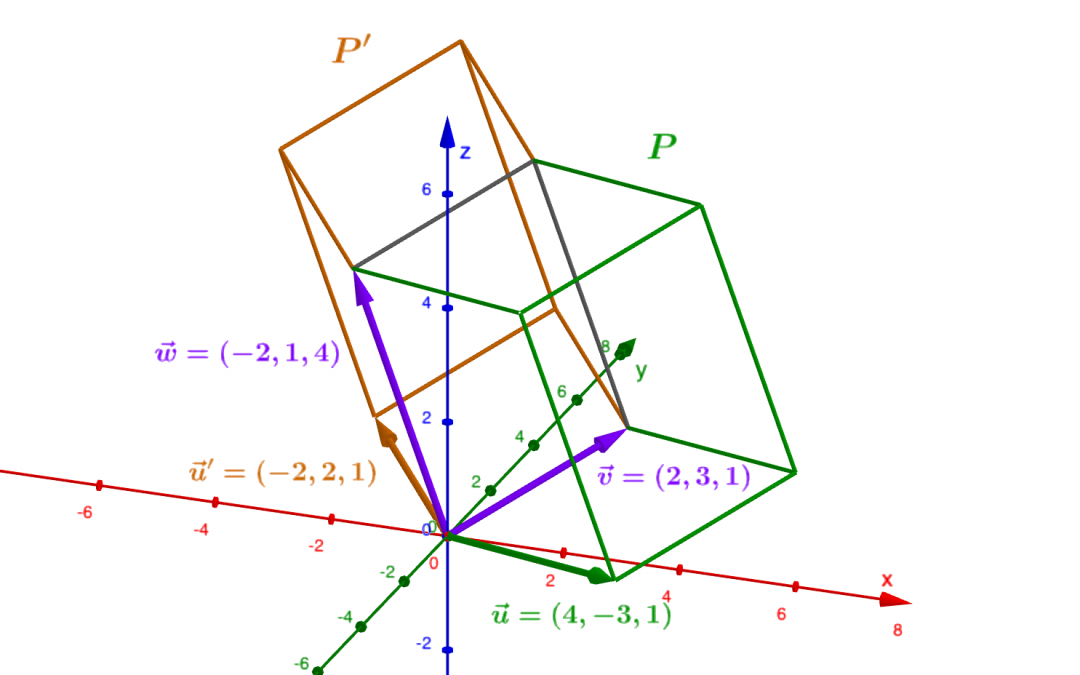
Le plan euclidien acquiert une orientation naturelle par le choix d’une base, que l’on peut qualifier de directe ou d’indirecte. Cette orientation se manifeste à travers le signe du déterminant de la base, correspondant à l’aire algébrique du...
par Jean Barbet | Nov 29, 2023 | Algèbre, Géométrie, Trigonométrie
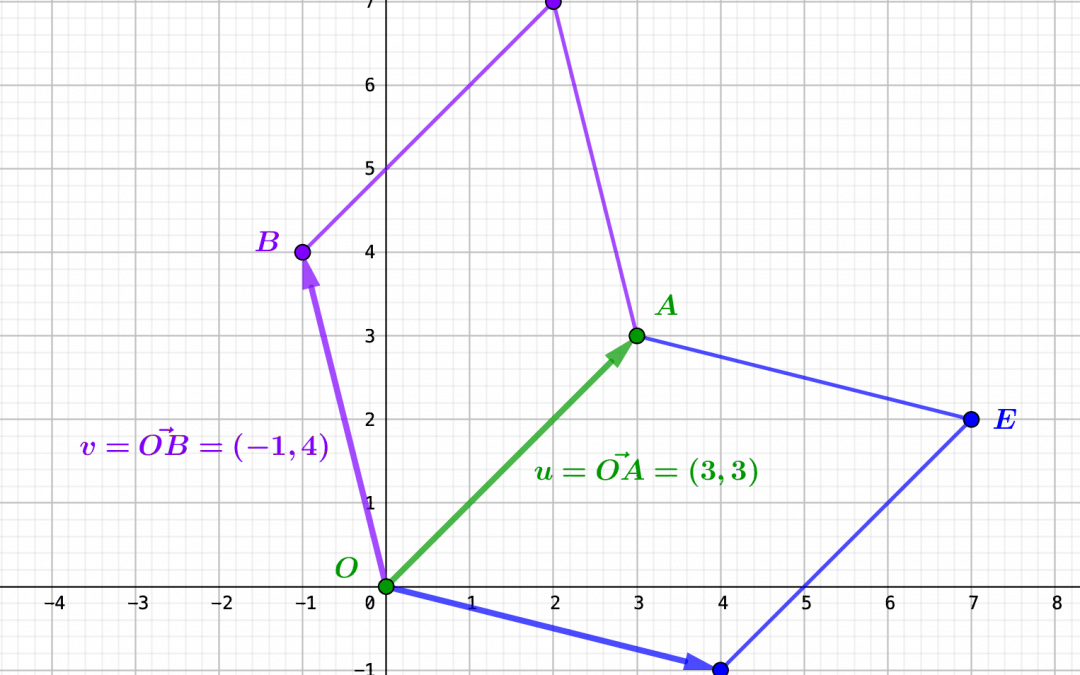
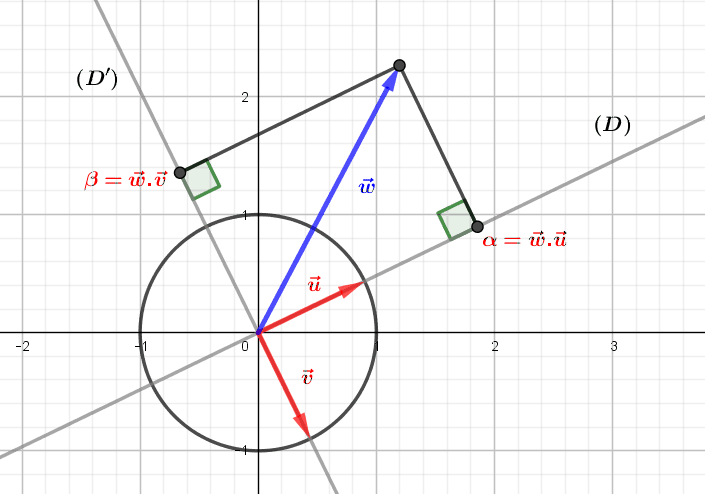
Le produit scalaire et le déterminant sont des concepts clés de l’algèbre linéaire dans le plan euclidien, offrant une compréhension profonde des relations entre deux vecteurs $u$ et $v$. Lorsque ces vecteurs sont unitaires, leur produit scalaire et déterminant...
par Jean Barbet | Juil 3, 2023 | Algèbre, Géométrie
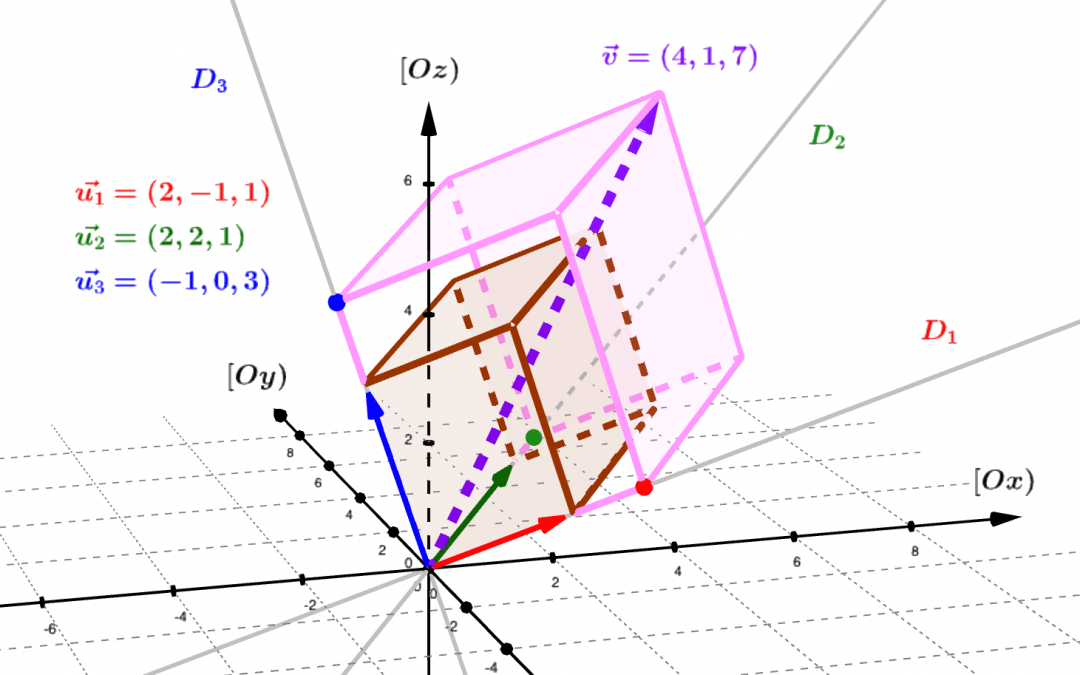
Comme dans le plan euclidien $\mathbb R^2$ , il existe dans l’espace euclidien $\mathbb R^3$ une infinité de bases ou « systèmes de représentation » des vecteurs : l’espace étant intuitivement de dimension 3, ces bases sont toujours formées de 3 vecteurs...
par Jean Barbet | Mai 22, 2021 | Algèbre, Géométrie
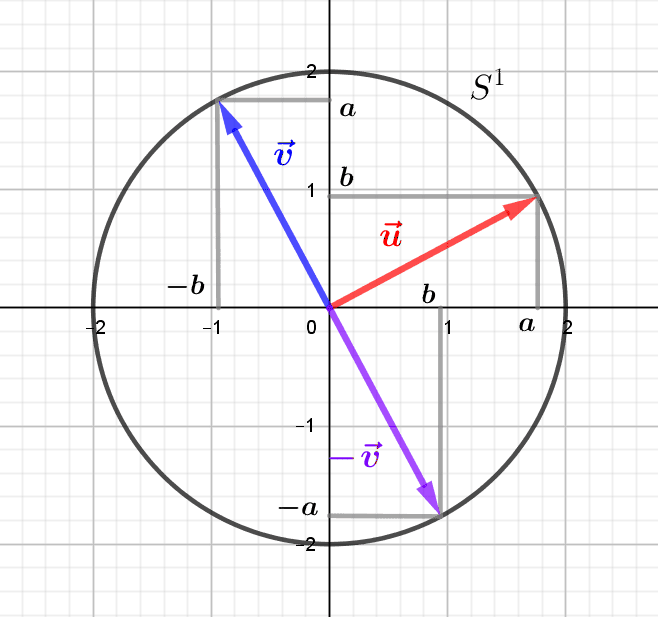
Les transformations linéaires du plan euclidien sont les applications linéaires inversibles, c’est-à-dire de déterminant non nul. Elles permettent de passer d’une base du plan à une autre, et les transformations orthogonales, c’est-à-dire les...
par Jean Barbet | Mai 7, 2021 | Algèbre, Géométrie
La représentation du plan euclidien par le produit cartésien \(\mathbb R^2\) permet de décomposer tout vecteur du plan en deux coordonnées, son abscisse et son ordonnée. Cette décomposition est liée à un « système de représentation » particulier et naturel,...






