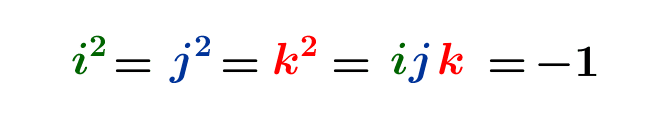
par Jean Barbet | Mar 27, 2024 | Algèbre, Nombres
Les propriétés des polynômes à une indéterminée sur un corps sont analogues à celles des nombres entiers relatifs. En exploitant cette analogie à partir de la notion de polynôme irréductible, on en tirer des informations précieuses sur l’arithmétique des...

par Jean Barbet | Mar 7, 2024 | Algèbre, Ensembles, Fonctions, Nombres
Les fractions rationnelles à une indéterminée apparaissent à la convergence de la théorie des fonctions rationnelles et de la théorie des polynômes. En généralisant la construction des nombres rationnels à partir des nombres entiers relatifs, on les construit comme...

par Jean Barbet | Juin 6, 2023 | Algèbre, Nombres
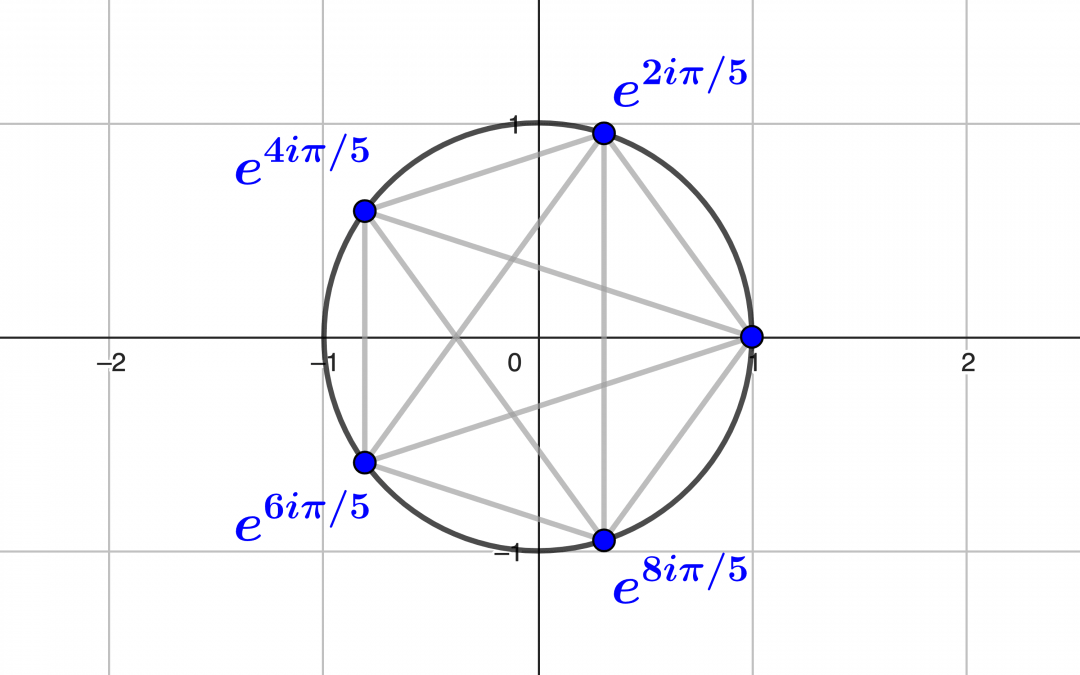
Les corps finis traduisent sur le plan structurel certaines propriétés arithmétiques et servent de « corps de restes » en théorie des nombres. Par analogie avec les corps $\mathbb R$ des nombres réels et $\mathbb C$ des nombres complexes, le nombre $-1$ peut y...
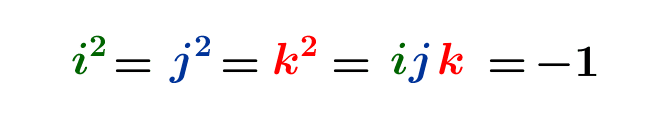
par Jean Barbet | Mar 19, 2021 | Algèbre
La multiplication complexe se prolonge naturellement à une multiplication en quatre dimensions, qui définit sur l’espace \(\mathbb R^4\) la structure de l’algèbre \(\mathbb H\) des quaternions de Hamilton. Cette multiplication s’interprète...