par Jean Barbet | Août 30, 2024 | Analyse, Fonctions
La notion de limite est la base de l’analyse réelle, c’est-à-dire de la théorie des fonctions à valeurs dans l’ensemble $\mathbb R$ : elle permet entre autres de définir les notions de continuité et de dérivation des fonctions d’une variable...
par Jean Barbet | Juin 18, 2024 | Analyse, Fonctions
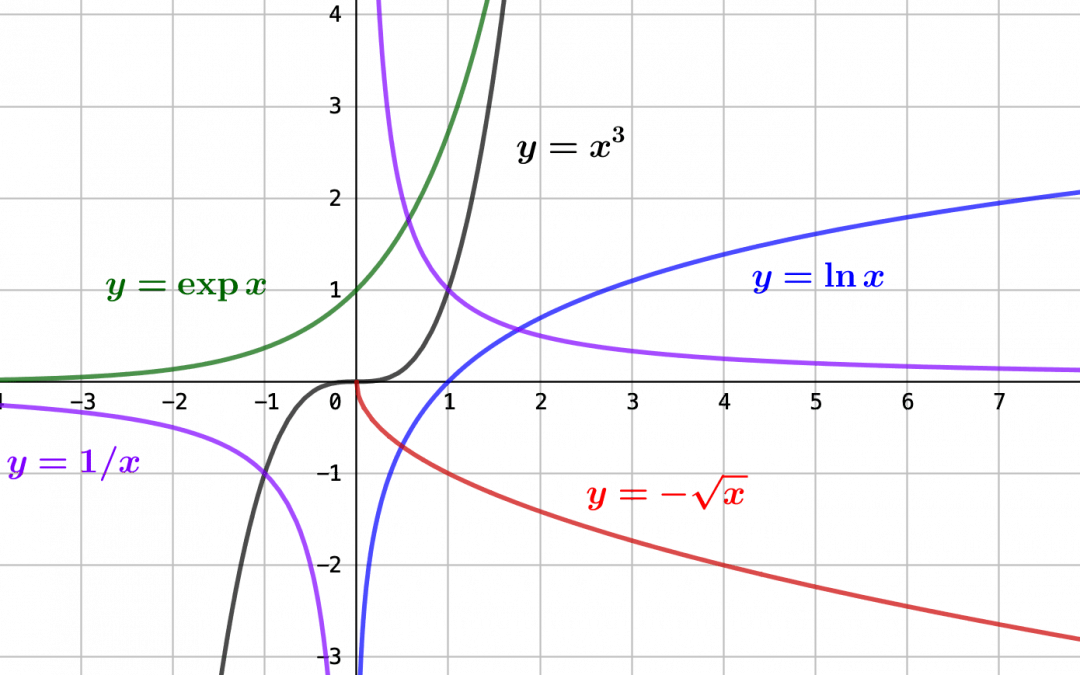
Les propriétés de l’analyse des fonctions d’une variable réelle sont celles qui sont associées à la structure de la droite réelle. L’ordre entre nombres réels, représentation de l’ordre entre les grandeurs naturelles, est l’élément...
par Jean Barbet | Avr 30, 2024 | Analyse, Ensembles, Nombres
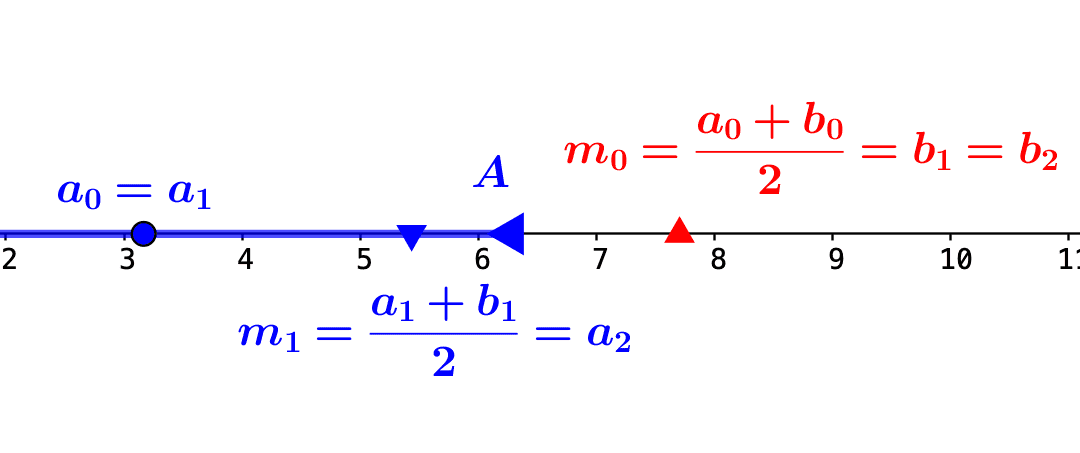
L’ensemble des nombres réels, quelle que soit la manière dont il est présenté, défini ou construit, n’est pas une multiplicité « amorphe », mais il vient avec une « structure » naturelle, héritée en dernière analyse de la structure arithmétique de...
par Jean Barbet | Déc 23, 2021 | Nombres
Dans cet article, nous abordons la question du « comptage » des nombres réels, autrement dit de la détermination du cardinal de l’ensemble \(\mathbb R\). Celui-ci est strictement supérieur au cardinal de l’ensemble des nombres rationnels, ce que nous...
