L’ensemble $\mathbb Z$ des nombres entiers relatifs [C1.III.2]
Dans la première section de ce chapitre, nous avons énoncé rigoureusement les trois axiomes de Peano, concernant la fonction successeur $s:\mathbb N\to \mathbb N$, $n\mapsto n+1$, et nous en avons déduit de nombreuses propriétés de l’ensemble $\mathbb N$, ainsi qu’une définition des opérations usuelles $+$ et $\times$, et des relations d’ordre naturel $\leq$ et $<$.
Ainsi, toute l’arithmétique naturelle, c’est-à-dire la théorie opératoire et relationnelle des nombres entiers naturels, repose sur ces trois axiomes, qui déterminent entièrement l’ensemble $\mathbb N$. Ceci illustre la puissance et la fécondité de cette « méthode axiomatique », connue depuis l’Antiquité et de manière intuitive à travers la géométrie d’Euclide, mais appliquée ici à la racine de l’édifice mathématique de manière totalement transparente, grâce à la théorie naïve des ensembles.
Or, on peut prolonger la description de la « structure naturelle de l’ensemble $\mathbb N$ » grâce à l’axiomatique de Peano, par la construction, parfaitement rigoureuse, des ensembles $\mathbb Z$, $\mathbb Q$, $\mathbb R$ et $\mathbb C$, et ceci sans axiomes supplémentaires. C’est ce que nous aborderons au second semestre, à partir d’un approfondissement de la théorie des ensembles.
Dans ce chapitre, nous allons plutôt adopter une approche axiomatique pour la description de l’ensemble $\mathbb Z$, auquel nous prolongerons les opérations et relations naturelles de l’ensemble $\mathbb N$. Nous pourrons alors exposer la théorie arithmétique élémentaire des nombres entiers relatifs, passablement plus élaborée que l’arithmétique des entiers naturels, qu’elle approfondit de manière lumineuse grâce à la soustraction. Et ceci, bien qu’elle soit contenue en germe dans les trois petits axiomes de Peano qui ouvrent ce livre.
1. Description axiomatique de l’ensemble $\mathbb Z$
Comme nous l’avons fait pour l’ensemble $\mathbb N$ dans la section [L’arithmétique de Peano] et dans les chapitres 1 et 2, nous admettons ici l’existence d’un ensemble $\mathbb Z$ des nombres entiers relatifs, que nous concevons de manière intuitive comme dans le chapitre 1 (Entrer dans l’Univers Mathématique) et qui contient l’ensemble $\mathbb N$ comme sous-ensemble.
A ce niveau du cursus, nous ne démontrons pas « l’existence » de cet ensemble, mais nous en donnons une description par des axiomes, comme nous l’avons fait pour l’ensemble $\mathbb N$.
1.1. Axiomatisation de $\mathbb Z$ à partir de l’addition
Dans le chapitre 1 (ibid.), nous avons énoncé quelques propriétés élémentaires de l’ensemble $\mathbb Z$. La formulation d’un système d’axiomes consiste à exprimer de telles propriétés mais en les choisissant judicieusement, de manière à décrire l’essentiel de la « structure arithmétique » de cet ensemble, qui nous intéresse dans ce volume.
Ici l’approche la plus naturelle nous paraît consister dans l’axiomatisation de l’addition (et de la soustraction) des entiers relatifs, c’est-à-dire que nous admettons l’existence d’une application $+:\mathbb Z\times\mathbb Z\to \mathbb Z$, prolongeant l’addition des entiers naturels, et possédant les propriétés axiomatiques suivantes :
Axiome 4
i) Pour tout $n\in\mathbb Z$ on a $0+n=n$
ii) Pour tous $n,m\in\mathbb Z$, on a $n+m=m+n$ (l’addition est commutative)
iii) Pour tous $n,m,k\in\mathbb Z$, on a $(n+m)+k=n+(m+k)$ (l’addition est associative)
iv) Pour tout $n\in\mathbb Z$, il existe $m\in \mathbb Z$ tel que $n+m=0$ (tout élément possède un opposé pour l’addition).
Remarque 1.1
Dire que l’addition des entiers relatifs prolonge celle des entiers naturels, cela signifie que pour $n,m\in\mathbb N$, le résultat de l’opération $n+m$ dans $\mathbb Z$ (puisque $\mathbb N\subseteq\mathbb Z$) est la somme $n+m$ telle qu’elle a été définie à la section [C1.III.1, L’addition des entiers naturels], ou encore, que l’addition $+_\mathbb N:\mathbb N^2\to \mathbb N$ des entiers naturels est la restriction de $+$ à $\mathbb N$, soit $+_\mathbb N=+|_{\mathbb N}$.
Par la propriété (iv) de l’axiome 4, tout nombre entier relatif possède un opposé pour l’addition : c’est la propriété fondamentale que ne possède pas l’ensemble $\mathbb N$ et qui fait l’intérêt arithmétique de l’ensemble $\mathbb Z$.
L’opposé additif $m$ d’un entier relatif $n$ est nécessairement unique : en effet, si $k\in\mathbb Z$ et $n+k=0$, alors on a $m=0+m$ (par (i)) $=m+0$ (par (ii)) $=m+(n+k)=(m+n)+k$ (par (iii)) $=(n+m)+k$ (par (ii)) $=0+k=k+0$ (par (ii)) $=k$ (par (i)). On note $-n$ l’opposé additif de $n$, et on définit la différence $n-m$ de deux entiers relatifs $n$ et $m$ comme l’entier relatif $n+(-m)$.
Définition 1.2
L’application $-:\mathbb Z\times\mathbb Z\to \mathbb Z$, qui associe à un couple d’entiers relatifs $(n,m)$ la différence $n-m=n+(-m)$, est la soustraction des entiers relatifs.
Les propriétés de l’axiome 1 ne suffisent pas à caractériser l’ensemble $\mathbb Z$, c’est-à-dire à le décrire de manière essentiellement unique. Pour compléter cette description axiomatique, il nous faut introduire un axiome fondamental qui permet de situer les entiers relatifs par rapport aux entiers naturels :
Axiome 5
Pour tout entier relatif $n$, soit $n$ est un entier naturel, soit $-n$ est un entier naturel.
On peut alors démontrer, dans le même esprit que [C1.III.1, Problème 1.5], que l’ensemble $\mathbb Z$ ainsi décrit est « essentiellement unique ».
La soustraction possède des propriétés analogues aux propriétés axiomatiques de l’addition et associées à celles-ci. Mentionnons trois d’entre elles, élémentaires mais essentielles :
Proposition 1.3
Soient $m$ et $n$ deux entiers relatifs.
o) On a $-(-n)=n$
i) On a $-(m+n)=-m-n$
ii) On a $-(m-n)=n-m$.
Démonstration
o) Par définition, $-(-n)$ est l’unique entier relatif $k$ tel que $(-n)+k=0$, soit $0=(-n)+(-(-n))=0$. En ajoutant $n$ aux deux membres, il vient $n=0+n=(-(-n)+(-n))+n$ (par commutativité de l’addition) $=-(-n)+((-n)+n)$ (par associativité de l’addition) $=-(-n)+(n+(-n))=(-n)+0=-(-n)$, ce qu’il fallait démontrer.
i) Par définition, l’entier $-(m+n)$ est l’unique entier relatif $k$ tel que $(m+n)+k=0$. Or on a $(m+n)+(-m-n)=(m+n)+(-n-m)$ (par commutativité de l’addition) $=m+(n+(-n-m))$ (par associativité de l’addition) $=m+((n+(-n))-m)$ (par associativité à nouveau) $=m+(0-m)=m-m=0$, donc $-(m+n)=-m-n$.
ii) Par (i), on a $-(m-n)=-m-(-n)=-m+n$ (par (o)) $=n-m$. $\square$
Notons enfin que tout nombre entier relatif $n$ peut toujours se représenter comme la différence de deux nombres entiers naturels. Par exemple, si $n\in\mathbb N$ on a $n=n-0$, et si $n\notin \mathbb N$ on a $-n\in\mathbb N$ par l’axiome 5, d’où $n=0-(-n)$ par la proposition 1.3. Ces représentations « standard » ne sont toutefois pas uniques, et il existe pour tout entier relatif $n$ une infinité de représentations de $n$ comme différence de deux entiers naturels. En effet, si $n\in\mathbb N$, alors pour tout $k\in\mathbb N$ on a $n=(n+k)-k$, tandis que si $n\in\mathbb Z-\mathbb N$, alors pour tout $k\in\mathbb N$ on a $n=k-(k-n)$ (puisque $-n\in\mathbb N$). Et on a bien sûr $0=k-k$ pour tout $k\in\mathbb N$.
Exemple 1.4
Le nombre entier $2$ se représente par exemple comme $2=5-3$ ou encore $2=128-126$, et de manière générale pour tout entier naturel $k$, comme $2=(2+k)-2$. De même, l’entier $-5$ se représente par exemple comme $-5=5-10$, ou encore $-5=247-252$, et de manière générale comme $-5=k-(k+5)$ pour tout entier naturel $k$.
1.2. L’ordre naturel dans $\mathbb Z$
Par définition, l’addition des entiers relatifs « prolonge » celle des entiers naturels, au sens où la seconde est la restriction de la première à l’ensemble $\mathbb N$.
Une autre façon de le concevoir est de considérer que l’addition des entiers relatifs est un prolongement de celle des entiers naturels.
Or, la « structure naturelle » de l’ensemble $\mathbb N$, décrite au premier chapitre, fait aussi apparaître l’ordre naturel, défini à partir de l’addition dans la section [C1.III.1, L’ordre sur les entiers naturels], sous sa forme d’ordre large $\leq$ ou d’ordre strict $<$ (dit linéaire).
Par analogie avec le prolongement de l’addition de l’ensemble $\mathbb N$ à l’ensemble $\mathbb Z$, on peut prolonger les relations d’ordre large et d’ordre strict à l’ensemble $\mathbb Z$.
Dans le chapitre 3 [C1.I.3 : Propriétés élémentaires des ensembles naturels] du Livre 1 (op. cit.), nous avons remarqué les analogies, les relations et les différences intuitives entre l’ordre naturel sur $\mathbb N$ et l’ordre naturel sur $\mathbb Z$. Nous utilisons ici ces remarques pour définir ce dernier :
Définition 1.5
Si $n$ et $m$ sont deux nombres entiers relatifs, on dit que :
i) $n$ est inférieur (ou égal) à $m$, ce qu’on note encore $n\leq m$, si il existe un entier naturel $k$ tel que $n+k=m$
ii) $n$ est strictement inférieur à $m$, ce qu’on note encore $n<m$, si il existe un entier naturel non nul $k$ tel que $n+k=m$.
Par [C1.III.1, définition 3.2 et proposition 3.6], on s’aperçoit immédiatement que l’ordre naturel et l’ordre strict dans $\mathbb Z$ prolongent respectivement l’ordre naturel et l’ordre strict dans $\mathbb N$, dans le sens où si $m$ et $n$ sont deux entiers naturels, alors on a $m\leq n$ dans $\mathbb Z$ si et seulement si $m\leq n$ dans $\mathbb N$, et $m<n$ dans $\mathbb Z$ si et seulement si $m<n$ dans $\mathbb N$.
Pour être absolument rigoureux, nous aurions du introduire une notation différente pour ces relations dans $\mathbb Z$ et leurs contreparties dans $\mathbb N$, mais cette dernière remarque permet précisément d’adopter de manière un peu abusive la même notation pour les relations d’ordre large et strict dans les deux ensembles.
Les propriétés élémentaires de l’ordre large sur $\mathbb Z$ sont les suivantes :
Proposition 1.6
Soient $m,n,k$ trois entiers relatifs.
o) On a $m\leq m$ (réflexivité)
i) Si $m\leq n$ et $n\leq m$, alors $m=n$ (antisymétrie)
ii) Si $m\leq n$ et $n\leq k$, alors $m\leq k$ (transitivité).
iii) On a $n\geq 0\Leftrightarrow n\in\mathbb N$.
Démonstration
o) On a $m+0=m$, et comme $0\in\mathbb N$, par définition on a $m\leq m$.
i) Par définition, il existe $k,l\in\mathbb N$ tels que $m+k=n$ et $n+l=m$, d’où $m+(k+l)=(m+k)+l=n+l=m$, et en ajoutant $-m$ aux deux membres on obtient $0=(-m)+m=(-m)+m+(k+l)=k+l$. Par [Axiomes et structure de l’ensemble $\mathbb N$, lemme 1(ii)], on a $k=l=0$, d’où $m=n$.
ii) Si $m\leq n$ et $n\leq k$, il existe $p,q\in\mathbb N$ tels que $n=m+p$ et $k=n+q$, si bien que $k=(m+p)+q=m+(p+q)$, et comme $p+q\in\mathbb N$, on a $m\leq k$.
iii) Si $n\geq 0$, alors par définition il existe $k\in\mathbb N$ tel que $0+k=n$, soit $k=n$, donc $n\in\mathbb N$. Inversement, si $n\in\mathbb N$ on a $0+n=n$, donc $0\leq n$. $\square$
Remarque 1.7
Par (iii), on a $\mathbb N=\mathbb Z_+=\{n\in\mathbb Z : n\geq 0\}$. Il s’ensuit qu’on a aussi $\mathbb Z-\mathbb N=\{n\in\mathbb Z : n<0\}$. Ainsi, si $n$ est un entier relatif, on a soit $n<0$, soit $n=0$, soit $n>0$.
En outre, la définition de l’ordre naturel par l’addition permet d’établir les relations suivantes entre les deux :
Proposition 1.8
Soient $m,n,k$ trois entiers relatifs.
i) Si $m\leq n$, alors $m+k\leq n+k$.
ii) Si $m<n$, alors $m+k<n+k$.
iii) On a $m\leq n$ si et seulement si $n-m\in\mathbb N$.
Démonstration
i) Si $m\leq n$, par définition il existe $p\in\mathbb N$ tel que $m+p=n$, d’où $(m+k)+p=m+(k+p)=m+(p+k)=(m+p)+k$ (par les propriétés de l’addition) $=n+k$; autrement dit, on a $m+k\leq n+k$.
ii) En exercice.
iii) Supposons que $m\leq n$ : par (i), on a $0=m-m=m+(-m)\leq n+(-m)=n-m$, donc $n-m\in\mathbb N$ par la proposition 1.6(iii). Inversement, si $n-m\in\mathbb N$, on a $0\leq n-m$, d’où $m=0+m\leq (n-m)+m$ (par (i)) $=n$. $\square$
L’axiome 5 se reformule sous la forme de la propriété de trichotomie suivante, déjà évoquée à propos de l’ensemble $\mathbb N$ ([C1.III.1, proposition 3.8]), et qui reflète le caractère « total » de l’ordre naturel :
Proposition 1.9
Soient $m$ et $n$ deux entiers relatifs. Alors un et un seul des cas suivants est vérifié :
i) $m<n$
ii) $m=n$
iii) $m>n$.
Démonstration
Il s’agit d’une simple reformulation de la remarque 1.7, en remarquant que $m<n$ si et seulement $m-n<0$, $m=n$ si et seulement si $m-n=0$ et $m>n$ si et seulement si $m-n>0$. $\square$
1.3. Exercices
Exercice 1.10
i) Démontrer que le seul entier relatif $n$ tel que $n=-n$ est $0$. Indication : raisonner par contraposée en supposant que $n\neq 0$, et distinguer les cas, selon que $n\in\mathbb N$ ou $n\notin \mathbb N$.
ii) Supposons que $m,n,k\in\mathbb Z$ et que $m< n$. Montrer que $m+k<n+k$ (proposition 3(ii)). En déduire que si $m\leq n$, alors $m+k\leq n+k$.
iii) Démontrer la deuxième partie de la remarque 2, et en déduire la proposition 3 (compléter la démonstration).
2. La multiplication et la divisibilité dans $\mathbb Z$
Désolé, vous n'avez pas accès à tout MATHESIS::Essentiel sans abonnement. Pour vous abonner, rendez-vous sur MATHESIS - Adhésion
4. Nombres premiers entre eux
Dans la section [C1.III.1, Nombres premiers entre eux], nous avons introduit le plus grand commun diviseur de deux nombres entiers naturels, et la notion de nombres entiers naturels premiers entre eux.
Si l’algorithme d’Euclide nous a donné le moyen de « calculer » théoriquement le p.g.c.d de deux nombres entiers naturels, nous n’avons pas approfondi la question de comment déterminer théoriquement si deux nombres entiers naturels sont premiers entre eux. L’algorithme d’Euclide nous donne un moyen pratique (calculer le p.g.c.d !) mais il existe un critère théorique fondamental, le théorème de Bézout.
La raison pour laquelle nous avons reporté cette question ici, est que l’étude de la « primalité relative » est plus naturelle dans le contexte de l’ensemble $\mathbb Z$ des nombres entiers relatifs, même en ce qui concerne les entiers naturels. En fait, le théorème de Bézout s’énonce à partir des nombres entiers relatifs, même si l’on ne considère que des entiers naturels.
Nous reprenons donc ici l’étude des nombres premiers entre eux pour l’approfondir, en étendant les définitions adéquates déjà introduites pour les entiers naturels.
Nous commençons l’arithmétique des entiers relatifs par cette question, car elle nous permettra d’avancer sur la théorie des nombres premiers, où nous démontrerons le théorème de Gauss sur la décomposition en nombres premiers, grâce au lemme d’Euclide.
Définition 4.1
i) Si $m$ et $n$ sont deux entiers relatifs non tous deux nuls, le plus grand commun diviseur de $m$ et $n$ est le p.g.c.d de $|m|$ et $|n|$. On le note aussi $pgcd(m,n)$ ou encore $m\wedge n$.
ii) On dit que deux entiers relatifs $m$ et $n$ sont premiers entre eux, si $m\wedge n=1$.
Remarque 4.2
o) Le p.g.c.d de deux entiers relatifs $m$ et $n$ quelconques est donc toujours un entier naturel.
i) Cette définition est encore parfaitement analogue à la définition introduite pour les entiers naturels : le p.g.c.d des entiers relatifs $m$ et $n$ est ici encore le plus grand entier relatif $d$ tel que $d$ divise à la fois $m$ et $n$ (voir les exercices).
ii) Nous verrons dans cette section que le p.g.c.d de $m$ et $n$ est également un plus grand diviseur commun de $m$ et $n$ au sens de la divisibilité. Autrement dit, on a $m\wedge n|m,n$, et si $d\in\mathbb Z$ divise à la fois $m$ et $n$, alors $d$ divise $m\wedge n$. Or, cette propriété est également vraie de $-m\wedge n$, si bien que sur le plan de la divisibilité, l’ordre naturel dans $\mathbb Z$ n’est pas très pertinent : nous aurions pu définir un p.g.c.d de $m$ et $n$ comme un entier relatif ayant cette propriété. Comme il n’existe que deux tels entiers relatifs, on choisit le plus grand pour l’ordre naturel, c’est-à-dire celui qui est positif.
Voici le critère fondamental de primalité relative entre deux nombres entiers relatifs, que nous démontrons à l’aide de l’algorithme d’Euclide sur les nombres entiers naturels.
Théorème 4.3 [Bézout]
Si $m$ et $n$ sont deux entiers relatifs non nuls, alors il existe deux entiers relatifs $u$ et $v$ tels que $pgcd(m,n)=mu+nv$.
Démonstration
Supposons d’abord que $m,n\in\mathbb N$. On a soit $n\leq m$ soit $m\leq n$, et dans les deux cas on a $pgcd(m,n)=pgcd(n,m)$, donc quitte à intervertir $m$ et $n$ si nécessaire on peut supposer que $n\leq m$ (l’autre cas est traité de manière similaire), donc $m>0$. Soit $(r_i)_\mathbb N$ la suite obtenue à partir de l’algorithme d’Euclide appliqué à $m$ et $n$ (section [C1.III.1, Nombres premiers entre eux], op. cit.). Si $r_1=0$, on a $m=nq_1+r_1=nq_1$, donc $n|m$ et pour $u=0$ et $v=1$, on a bien alors $um+vn=n=pgcd(m,n)$. Si $r_1\neq 0$, par définition on a $m=nq_1+r_1$, d’où $r_1=m+n(-q_1)$ : par [C1.III.1, proposition 6.10], si $r_2=0$ on a $pgcd(m,n)=r_1$, qui est de la forme désirée. Supposons maintenant que $r_2\neq 0$, et soit $N$ le plus grand entier naturel $i\geq 2$ tel que $r_i\neq 0$, par [C1.III.1, lemme 6.9]. On suppose que pour tout $i=0,\ldots,N-1$, il existe $u_i,v_i\in \mathbb Z$ tels que $r_i=mu_i+nv_i$. Par définition, on peut écrire $r_{N-2}=r_{N-1}q_N+r_N$, d’où $r_N=r_{N-2}-r_{N-1}q_N=mu_{N-2}+nv_{N-2}-q_N(mu_{N-1}+nv_{N-1})=m(u_{N-2}-q_N u_{N-1})+n(v_{N-2}-q_N v_{N-1})$, qui est encore de la forme désirée. Par [C1.III.1, proposition 6.10] à nouveau, on a $r_N=pgcd(m,n)$, d’où le résultat dans ce cas.
En général, si $m,n\in\mathbb Z$, on a $|m|,|n|\in\mathbb N$ : par le cas précédent, il existe $u,v\in\mathbb Z$ tels que $pgcd(m,n)=pgcd(|m|,|n|)=|m|u+|n|v$. Par définition de la valeur absolue, il existe donc des entiers relatifs $u’,v’\in\mathbb Z$ tels que $pgcd(m,n)=mu’+nv’$. En effet, si $|m|=m$ et $|n|=n$, alors $u’=u$ et $v’=v$ conviennent; si $|m|=-m$ et $|n|=n$, alors $u’=-u$ et $v’=v$ conviennent; si $|m|=m$ et $|n|=-n$, alors $u’=u$ et $v’=-v$ conviennent; et si $|m|=-m$ et $|n|=-n$, alors $u’=-u$ et $v’=-v$ conviennent. $\square$
Remarque 4.4
L’essentiel de la démonstration porte sur le cas où $m,n\in\mathbb N$, et l’étude du second cas (où $r_1\neq 0$) montre que l’introduction des entiers relatifs est essentielle, puisqu’il faut utiliser l’opposition du quotient $q_1$ (dans le cas où $r_2=0$) ou une soustraction (dans le cas où $r_2\neq 0$).
Du théorème de Bézout on tire le critère théorique suivant, qui permet de caractériser les couples $(m,n)$ d’entiers relatifs premiers entre eux :
Corollaire 4.5
Deux entiers relatifs non nuls $m$ et $n$ sont premiers entre eux si et seulement si il existe $u,v\in\mathbb Z$ tels que $mu+nv=1$.
Démonstration
Par le théorème de Bézout (théorème 4.3), il existe $u,v\in\mathbb Z$ tels que $mu+nv=pgcd(m,n)$. Si $m$ et $n$ sont premiers entre eux, alors $pgcd(m,n)=1$, d’où l’égalité.
Inversement, si il existe $u,v\in\mathbb Z$ tels que $mu+nv=1$, notons $d=pgcd(m,n)$ : comme $d$ divise à la fois $m$ et $n$, il divise $mu+nv$, si bien que $d\mid 1$ et finalement, $d=1$ et $m$ et $n$ sont premiers entre eux. $\square$
Un autre corollaire du théorème de Bézout permet de déterminer quand une équation de la forme $ax+by=c$ possède des solutions entières en $x$ et $y$.
Corollaire 4.6
Si $m$, $n$ et $c$ sont trois entiers relatifs et $m$ et $n$ sont non nuls, alors l’équation $mx+ny=c$ possède une solution $(x,y)\in\mathbb Z^2$ si et seulement si $m\wedge n |c$.
Démonstration
Supposons que cette équation possède une solution $(u,v)\in\mathbb Z^2$, de sorte que l’on a l’égalité $mu+nv=c$ : comme $m\wedge n|m,n$, on a $m\wedge n|mu+nv=c$.
Réciproquement, si $m\wedge n|c$ il existe $k\in\mathbb Z$ tel que $c=k.(m\wedge n)$; par le théorème 4.3, soient $u,v\in\mathbb Z$ tels que $mu+nv=m\wedge n$ : on a $k.(mu+nv)=k.(m\wedge n)=c$, donc le couple $(ku,kv)$ est une solution de d’équation $mx+ny=c$. $\square$
La démonstration du théorème de Bézout montre qu’ici comme ailleurs, cela n’aurait pas trop de sens de séparer artificiellement l’arithmétique dans l’ensemble $\mathbb N$ de l’arithmétique dans l’ensemble $\mathbb Z$. Comme le montrera la section suivante, à propos de la décomposition en nombres premiers, il faut plutôt voir la seconde comme un « approfondissement » de la première.
Trouver une relation de Bézout entre deux entiers relatifs $m$ et $n$ non nuls, c’est trouver deux entiers relatifs $u$ et $v$ tels que $um+vn=pgcd(m,n)$. En utilisant la stratégie de la seconde partie de la démonstration du théorème de Bézout 4.3, il suffit de savoir le faire pour $m,n\in\mathbb N$.
Ceci peut se faire grâce à l’algorithme d’Euclide : écrivons le complètement pour deux entiers naturels $m\geq n>0$ comme dans la section [C1.III.1, Nombres premiers entre eux] (op. cit.). Nous définissons alors deux suites $(q_i)$ et $(r_i)$ d’entiers comme suit. On pose $n=r_0$, on écrit $m=nq_0+r_1$ la division euclidienne de $m$ par $n$ (donc avec $r_1<n$) et pour tout $n\geq 1$, on définit $q_n$ et $r_{n+1}$ en écrivant la division euclidienne de $r_{n-1}$ par $r_n$ sous la forme $r_{n-1}=r_nq_n+r_{n+1}$ (donc avec $r_{n+1}<r_n$).
Si on note $N$ l’indice du dernier reste non nul (par [C1.III.1, lemme 6.7]), on dispose ainsi de $N$ relations $m=nq_0+r_1$, $r_0=n=r_1q_1+r_2$, $r_1=r_2q_2+r_3$, … et $r_{N-2}=r_{N-1}q_{N-1}+r_N$. On en tire $r_1= m-nq_0$ et $r_2=n-r_1q_1=n-(m-nq_0)q_1=n(1+q_0q_1)+m(-q_1)$, puis $r_3=r_1-r_2q_2$, soit $r_3=(m-nq_0)-q_2(n(1+q_0q_1)+m(-q_1))=m(1+q_1q_2)+n(-q_0).(1+q_1q_2)$. De proche en proche, en substituant à $r_n$ la valeur obtenue par l’équation $r_{n-2}=r_{n-1}q_{n-1}+r_n$, soit $r_n=r_{n-2}-r_{n-1}q_{n-1}$, pour $n=2,\ldots,N$, on obtient une relation de Bézout entre $m$ et $n$.
Exemple 4.7
Cherchons une relation de Bézout entre $561$ et $-381$, en appliquant l’algorithme d’Euclide à $m=561$ et $n=385$. On obtient $561=385.1+176$, $385=176.2+33$, $176=33.5+11$ et $33=11.3$. On en tire $176=561-385$ et $33=385-176.2=385-(561-385).2=561.(-2)+385.3$. On a également $11=176-33.5=(561-385)-(385.3-561.2).5=561.11+385.(-16)$, relation de Bézout entre $561$ et $385$, puisque $11=pgcd(561,385)=pgcd(561,-385)$. On en déduit la relation de Bézout $561.11+(-385).16=11$.
La figure suivante donne une interprétation géométrique du théorème de Bézout basée sur la géométrie affine (voir le Livre 4).
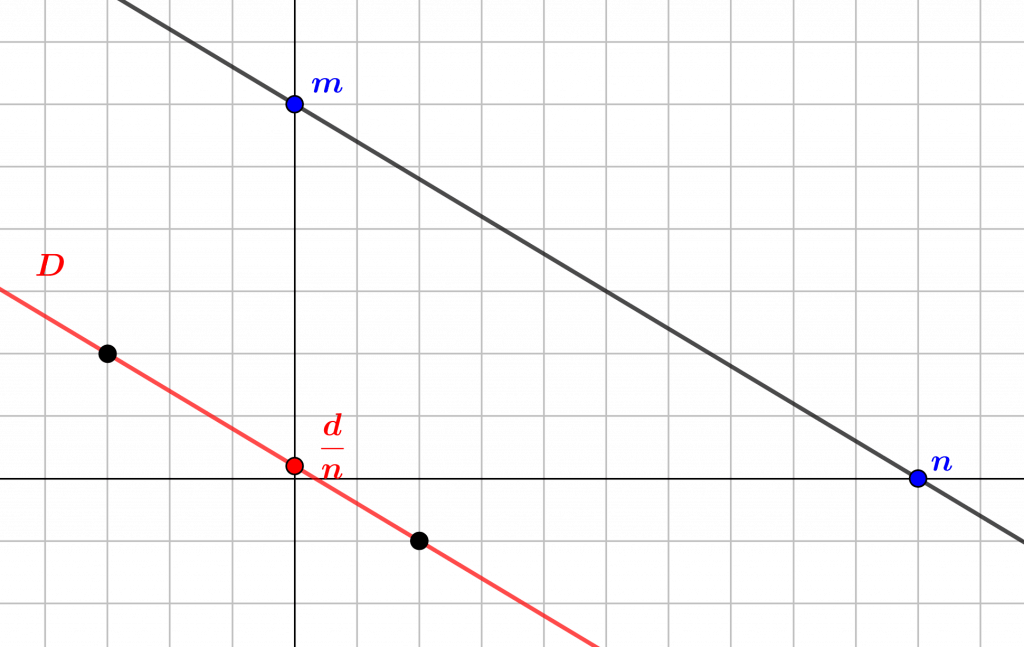
La fin de cette section est consacrée à établir le lemme de Gauss (théorème 4.10), qui est « l’instrument » essentiel du lemme d’Euclide (lemme 5.6), et donc du théorème de Gauss 5.7 sur la décomposition des entiers relatifs en facteurs premiers.
Proposition 4.8
Si $m,n$ et $p$ sont trois entiers relatifs non nuls, alors :
i) $m\wedge n$ est un plus grand diviseur commun de $m$ et $n$ au sens de $|$; autrement dit, pour tout $d\in\mathbb Z$ tel que $d|m,n$, on a $d|m\wedge n$
ii) On a $|p|\times(m\wedge n)=(p\times m)\wedge (p\times n)$.
Démonstration
i) Par le théorème de Bézout (théorème 4.3), il existe $u,v\in\mathbb Z$ tels que $m\wedge n=mu+nv$. Supposons que $d\in \mathbb Z$ est un diviseur commun de $m$ et $n$ : on a $d|mu,nv$, donc $d|mu+nv=m\wedge n$.
ii) Si $d\in \mathbb Z$ et $d|m,n$, alors on a $pd|pm,pn$, d’où $pd|(pm\wedge pn)$ par (i); en particulier, on a $p\times (m\wedge n)|(pm\wedge pn)$. Inversement, comme $p|pm\wedge pn$ puisque $p|pm,pn$, il existe $q\in\mathbb Z$ tel que $pq=pm\wedge pn$, donc aussi $pq|pm$ et $pq|pn$ : il existe $u,v\in \mathbb Z$ tels que $pm=upq$ et $pn=vpq$, d’où $p(m-uq)=0$ et $p(n-vq)=0$, si bien que $m=uq$ et $n=vq$ par intégrité ([Axiomes et structure de l’ensemble $\mathbb Z$, théorème 2.6]), et finalement $q|m,n$. Par (i) à nouveau, on a $q|m\wedge n$, d’où $pm\wedge pn=pq|p\times (m\wedge n)$. Par conséquent, on a à la fois $p\times (m\wedge n)|pm\wedge pn$ et $pm\wedge pn|p\times(m\wedge n)$, d’où $p\times (m\wedge n)=pm\wedge pn$ ou $p\times (m\wedge n)=-(pm\wedge pn)$, soit $|p|\times (m\wedge n)=|p\times(m\wedge n)|=(p\times m)\wedge (p\times n)$ (le second membre de l’égalité est toujours positif). $\square$
Remarque 4.9
Lorsque $m,n,p\in\mathbb N$, on peut supprimer les valeurs absolues dans (ii).
Théorème 4.10 [Lemme de Gauss]
Si $m,n$ et $p$ sont des entiers relatifs non nuls, et si $m$ divise $np$ et $m$ et $n$ sont premiers entre eux, alors $m$ divise $p$.
Démonstration
Par la proposition 4.8(ii), on a $mp\wedge np=|p|\times(m\wedge n)$ et comme $m\wedge n=1$, on en déduit que $mp\wedge np=|p|$. Mais $m|np$ par hypothèse, si bien que $m|(mp\wedge np)=|p|$ par la proposition 4.8(i), donc $m|p$ également. $\square$
Remarque 4.11
Ici, le contenu essentiel du théorème a déjà été traité dans la proposition 1.
4.1. Exercices
Exercice 4.12
i) Si $m$ et $n$ sont deux entiers relatifs non tous deux nuls, démontrer que le p.g.c.d $m\wedge n$ de $m$ et $n$ est le plus grand entier relatif $d$ tel que $d$ divise à la fois $m$ et $n$, autrement dit que $d|m,n$ et que si $k\in\mathbb Z$ et $k|m,n$, alors $k\leq d$.
ii) Trouver une relation de Bézout entre $63$ et $-175$.
iii) Montrer que $77$ divise $15400$ et que $77$ et $39$ sont premiers entre eux. En déduire que $77$ divise $385$.
5. Nombres premiers
5.1. Puissances des entiers relatifs
Désolé, vous n'avez pas accès à tout MATHESIS::Essentiel sans abonnement. Pour vous abonner, rendez-vous sur MATHESIS - Adhésion

Les propriétés énoncées à la proposition 5 à propos de l’ensemble $\mathbb Z$ des entiers relatifs sont celles de « structures mathématiques » appelées « anneaux commutatifs unitaires », fondamentales en arithmétique, algèbre et géométriques. Ces structures seront abordées dès le Cycle 2 afin de donner une interprétation algébrique des résultats arithmétiques élémentaires que nous abordons ici.