L’ensemble $\mathbb N$ des nombres entiers naturels [C1.III.1]
Dans ce premier chapitre, nous abordons l’étude axiomatique de l’ensemble $\mathbb N$ des nombres entiers naturels. Dans le Livre 1, nous avons considéré que les nombres entiers naturels et leurs propriétés élémentaires nous étaient connus de manière intuitive, et qu’ils étaient ainsi des concepts mathématiques primitifs, au sens où on ne les définit pas mathématiquement. Nous conservons ici ce point de vue, et l’approche qui consiste à théoriser les propriétés des entiers naturels grâce à la théorie des ensembles, en considérant des propriétés globales de l’ensemble $\mathbb N$. Il est toutefois possible de réduire les propriétés qu’on doit admettre comme des principes indémontrables à un petit jeu de trois axiomes qu’on doit au mathématicien Giuseppe Peano. Nous allons voir comment, à partir de ces principes simples et transparents concernant la fonction successeur, il est possible de définir toute la « structure naturelle » de l’ensemble $\mathbb N$, et de développer des bases solides de l’arithmétique ou théorie des nombres. D’ailleurs, même si nous ne définissons pas mathématiquement les nombres entiers naturels, les axiomes de Peano déterminent cet ensemble de manière « essentiellement unique », et c’est tout ce qu’il nous faut en mathématique.
1.Les axiomes de Peano comme postulats
Lorsque nous avons défini la notion d’ensemble infini dans le cours sur le fini et l’infini (Livre 2), l’ensemble $\mathbb N$ des nombres entiers naturels a joué un rôle essentiel, à la fois comme « frontière » entre les ensembles finis et infinis, et comme exemple fondamental d’ensemble infini permettant de caractériser, c’est-à-dire d’identifier, tous les autres. Pour montrer que $\mathbb N$ est infini, nous avons du faire usage du principe de récurrence, qui est en quelque sorte une propriété de la fonction successeur $s:\mathbb N\to \mathbb N$. Nous allons ici l’exposer précisément et l’exploiter pour décrire l’ensemble $\mathbb N$ et fonder notre étude de l’arithmétique élémentaire. Il est possible de rassembler des propriétés essentielles de la fonction successeur, appelées « axiomes », qui permettent de la décrire complètement, et à partir de là, de « reconstituer » toute la « structure » opératoire ($+$ et $\times$) et relationnelle ($\leq$ et $|$) classique de l’ensemble $\mathbb N$.
1.1.Les axiomes de l’arithmétique de Peano
La liste d’axiomes que nous présentons dans cette section est due au mathématicien italien Giuseppe Peano. L’idée sous-jacente à cette démarche « axiomatique » est que l’usage que nous avons fait de la fonction successeur repose sur des propriétés intuitives, indémontrables : ces propriétés déterminent en fait ce que nous « entendons » par la fonction successeur ! Au point de vue où nous nous plaçons, nous devrions peut-être plutôt appeler ces propriétés des postulats : elles dénotent ce que nous affirmons, ce que nous « croyons », à propos de la fonction successeur. Quoiqu’il en soit, ces axiomes ou postulats sont des conditions sous lesquelles nous pouvons fonder la mathématique comme science, en commençant par l’arithmétique. Ces conditions sont nécessaires, au sens où nous n’avons pas le choix d’adopter une telle démarche pour bâtir les mathématiques : si nous rejetons ces axiomes, ou ce point de départ, il nous faudra en trouver d’autres, équivalents. Nous choisissons ici des axiomes simples, naturels et éprouvés, à propos de la fonction la plus simple possible sur le premier ensemble naturel de nombres.
Axiome 1
$0$ n’est le successeur d’aucun entier naturel. En d’autres termes, il n’existe pas d’entier naturel $n$ tel que $s(n)=0$.
Cet axiome dit en particulier que la fonction $s$ n’est pas surjective, puisque le nombre $0$ ne possède pas d’antécédent par $s$.
Axiome 2 PEANOSUCC}
Si deux entiers naturels $m$ et $n$ ont le même successeur, alors ils sont égaux. En d’autres termes, pour tous entiers naturels $m,n$, si $s(m)=s(n)$ alors $m=n$.
On peut reformuler cet axiome en disant que l’application successeur est injective. Sa co-restriction à son image est donc une bijection de $\mathbb N$ sur une partie propre de $\mathbb N$ : on reconnait ici la caractérisation intrinsèque d’un ensemble infini, que nous avons abordée à la fin du cours sur le fini et l’infini. Quelle est l’image $Im(s)$ de l’application successeur ? Pour le déterminer, il nous faut là encore faire appel à notre intuition. Or, il paraît évident que tout entier naturel non nul est le successeur d’un entier naturel ! Nous pourrions l’introduire comme un nouvel axiome, mais il s’agit d’une conséquence de l’axiome suivant, dit « principe de récurrence » :
Axiome 3 [Principe de récurrence (ou d’induction)]
Si $S$ est un sous-ensemble de $\mathbb N$ tel que : i) $0\in S$ ii) pour tout $n\in S$, $s(n)\in S$ (« étape de récurrence »), alors on a $S=\mathbb N$.
Les applications de ce principe, ubiquitaires dans toute la mathématique, clarifieront sa signification et sa fécondité, mais il exprime intuitivement que l’ensemble $\mathbb N$ est entièrement « parcouru » si nous l’énumérons à partir de $0$ et ajoutons chaque entier naturel successif, de manière indéfinie. On peut en déduire la détermination de l’image de $s$ :
Proposition 1.1
Si on admet le principe de récurrence, alors l’image de $s$ est $\mathbb N^*$, l’ensemble des entiers naturels non nuls.
Démonstration
Soit $S$ l’ensemble $\{0\}\cup Im(s)=\{0\}\cup\{n\in \mathbb N: \exists m\in\mathbb N,\ n=s(m)\}$. Si nous montrons que $S=\mathbb N$, alors tout entier naturel non nul est dans l’image de $s$, donc $Im(s)=\mathbb N^*$. Par définition, on a $0\in S$, et supposons que $n$ est un entier naturel, et que $n\in S$. Par définition, l’entier naturel $s(n)$ est dans $S$ ! Par le principe de récurrence, l’ensemble $S$ est $\mathbb N$ tout entier, et la proposition est démontrée. $\square$
Rappelons que le successeur $s(n)$ d’un entier naturel $n$ est l’entier naturel que nous notons aussi $n+1$, étant entendu que $1$ est le successeur de $0$. En effet, lorsque nous définirons dans la suite l’addition à partir du successeur, nous verrons que $s(n)$ est par définition égal à $n+1$. Le principe de récurrence est essentiellement utilisé en mathématique de deux manières différentes, que nous avons déjà rencontrées et pratiquées : pour les démonstrations par récurrence d’une part, pour les définitions par récurrence d’autre part. Une démonstration par récurrence consiste à démontrer qu’une propriété $P(n)$, qui dépend de l’entier naturel $n$, est vraie quel que soit $n\in\mathbb N$, c’est-à-dire universellement valide. Cela revient à démontrer que l’ensemble $S$ des entiers naturels $n$ qui ont la propriété $P(n)$, soit $S=\{n\in\mathbb N : P(n)\}$, est $\mathbb N$ tout entier. Le raisonnement par récurrence consiste alors à appliquer le principe de récurrence à l’ensemble $S$.
1.2.Le théorème de récurrence
En ce qui concerne les définitions par récurrence, l’explication est un peu plus délicate et la justification repose sur le théorème de récurrence que nous exposons ci-après. La définition par récurrence consiste essentiellement à « construire » une application $u$ de $\mathbb N$ dans un ensemble $E$ (ce qu’on appelle une suite d’éléments de $E$) à partir de deux données : i) Le choix du « premier terme » de la suite, c’est-à-dire $u(0)$, qui est un élément donné de $E$ ii) Un « procédé » de définition de la valeur $u(n+1)$ de la suite au rang $s(n)=n+1$ lorsqu’on connaît sa valeur $u(n)$ au rang $n$. La seconde donnée peut se formaliser comme celle d’une application $f$ de $E$ dans lui-même : une telle fonction fournit bien un moyen de « transformer » une valeur $u(n)$ de la suite en un autre élément de $E$, même si dans cette approche la fonction $f$ comme procédé est définie pour tous les éléments de $E$, tandis qu’on n’en a besoin a priori que pour les valeurs de la suite. Ceci explique la formulation du théorème suivant, dont la démonstration est un peu exigeante mais très instructive :
Théorème 1.2 [Théorème de récurrence]
Si $f:E\to E$ est une application d’un ensemble dans lui-même et $a\in E$, il existe une unique application $g:\mathbb N\to E$ telle que $g(0)=a$ et $g(s(n))=f(g(n))$ pour tout $n\in\mathbb N$.
Démonstration
La démonstration se fait en deux étapes. i) On montre par récurrence que pour tout $n\in\mathbb N$, il existe une unique application $h:[[0,n]]\to E$ telle que $h(0)=a$ et pour tout $i<n$, $h(s(i))=f(h(i))$. Pour $n=0$, la seule fonction $h:[[0,0]]=\{0\}\to E$ telle que $h(0)=a$ (la deuxième condition est « vide ») est définie par cette condition, donc la propriété est vérifiée au rang $n=0$. Supposons qu’elle le soit au rang $n$ : il existe une unique fonction $h:[[0,n]]\to E$ telle que $h(0)=a$ et $h(s(i))=f(h(i))$ pour tout $i<n$. Définissons une fonction $g:[[0,n+1]]\to E$ en posant $g(i)=h(i)$ pour tout $i<n+1$ et $g(n+1)=f(h(n))$. On a $g(0)=h(0)=a$, et pour tout $i<n$, $g(s(i))=h(s(i))=f(h(i))$ par l’hypothèse de récurrence; comme $g(s(n))=f(g(n))$ par définition, $g:[[0,n+1]]\to E$ possède la propriété voulue. Supposons que $k:[[0,n+1]]\to E$ soit une autre fonction avec ces propriétés : en particulier, on a $k(0)=a$ et pour tout $i<n$, $k(s(i))=f(k(i))$ et par hypothèse de récurrence, $h$ étant unique avec ces propriétés la restriction $k|_{[[0,n]]}$ de $k$ à $[[0,n]]$ est égale à $h$. Il s’ensuit aussi que $k(n+1)=k(s(n))=f(k(n))=f(h(n))=f(g(n))=g(s(n))=g(n+1)$, donc finalement $k=g$ et l’unicité aussi est démontrée au rang $n+1$. On conclut par récurrence que la propriété est vérifiée pour tout $n\in\mathbb N$.
ii) On en déduit qu’il existe une unique application $g:\mathbb N\to E$ telle que $g(0)=a$ et pour tout $n\in\mathbb N$, $g(s(n))=f(g(n))$. Pour cela, soit $n\in\mathbb N$ : par (i) il existe une unique fonction $h_n:[[0,n]]\to E$ avec les propriétés données, et on définit alors $g(n)$ comme $h_n(n)$. On obtient ainsi une fonction $g:\mathbb N\to E$. Par définition, on a $g(0)=h_0(0)=a$, et pour tout $n\in\mathbb N$, on a $g(s(n))=h_{s(n)}(s(n))=f(h_{s(n)}(n))=f(h_n(n))$ (car par unicité dans (i), on a $h_{s(n)}|_{[[0,n]]}=h_n$) $=f(g(n))$, donc $g$ a les propriétés voulues. En ce qui concerne l’unicité, si $k:\mathbb N\to E$ est une application telle que $k(0)=a$ et $k(s(n))=f(k(n))$ pour tout $n\in\mathbb N$, on démontre facilement par récurrence que $\{n\in\mathbb N : g(n)=k(n)\}$ est l’ensemble $\mathbb N$ tout entier, et donc que $k=g$, et le théorème est démontré.
$\square$
Dans la pratique, la définition par récurrence procède par une « construction » du graphe $R$ de la suite $g$, soit une relation fonctionnelle $R$ sur $\mathbb N\times E$, pour laquelle pour tout $n\in\mathbb N$, il existe $x\in E$ avec $(n,x)\in R$. En principe, on définit $g(0)$ (on choisit un élément $a$ de $E$), à partir d’une propriété essentielle, et on décrit un procédé (la fonction $f$) qui permet de définir $g(n+1)$ à partir de $g(n)$, sous la forme d’une expression qui traduit les contraintes de définition de la fonction $g$. Par le théorème 1.2, l’unique fonction $g$ ayant les propriétés désirées est la suite qu’on définit par récurrence.
Exemple 1.3
Reprenons la définition par récurrence de l’expression $a^n$, pour $a$ un nombre réel et $n$ un entier naturel : on pose $a^0:=1$ et $a^{n+1}=a^n\times a$. Dans cette situation, on définit une application $g:\mathbb N\to \mathbb R$, qui associe à l’entier $n$ le nombre réel $a^n$. L’application $f:\mathbb R\to \mathbb R$ qui convient est la « multiplication par $a$ », qui associe à $x\in\mathbb R$ le nombre réel $a.x$. En posant $g(0)=1$ (valeur de $a^0$), le théorème 1.2 nous assure qu’il existe une seule fonction $g:\mathbb N\to \mathbb R$ telle que $g(0)=a$ et $g(n+1)=a.g(n)$ pour tout $n\in\mathbb N$ : c’est la fonction cherchée.
Terminons en précisant que la description de la fonction successeur par ces axiomes suppose qu’il est légitime, dans la théorie des ensembles ou le méta-univers, de poser l’existence d’une application de $\mathbb N$ dans lui-même ayant ces propriétés. Admettre l’existence d’un ensemble $\mathbb N$ de tous les entiers naturels est d’ailleurs déjà une supposition de ce genre, que nous complétons ici : nous (sup)posons – sans pouvoir le démontrer – qu’il est licite de travailler avec une telle fonction dans l’univers des objets mathématiques. A la racine de l’édifice mathématique, comme de tout discours scientifique, il faut faire un « pas de foi » dans la cohérence des principes élémentaires sur lesquels il faut bâtir, et qu’il n’est jamais possible de démontrer; ceci souligne que la créativité demeure un élément essentiel de l’activité scientifique, mathématique en particulier. Grâce à ces quelques axiomes très simples, nous entrons avec la théorie naïve des ensembles et l’axiomatique de Peano dans la construction rigoureuse de tout l’édifice mathématique : nous allons voir qu’il est désormais possible de définir toute la structure arithmétique naturelle et d’en redémontrer les propriétés élémentaires. La suite du semestre montrera également comment on peut « construire » tous les autres ensembles naturels $\mathbb Z,\mathbb Q,\mathbb R,\mathbb C$ et $\HH$ abordés au premier et au second cours à partir de la structure de $\mathbb N$ et de la théorie naïve des ensembles.

1.3.Exercices de la section
Exercice 1.4
Justifier le principe du raisonnement par récurrence à l’aide l’axiome 3. Autrement dit, si $P(n)$ est une propriété des entiers naturels $n$, telle que $P(0)$ est vraie, et telle que l’implication $P(n)\Rightarrow P(n+1)$ est universellement valide, expliquer pourquoi $P(n)$ est universellement valide, c’est-à-dire pourquoi l’énoncé $\forall n\in\mathbb N, P(n)$ est vrai.
Problème 1.5
On se propose ici de démontrer la « catégoricité » de l’axiomatique de Peano, autrement que la fonction successeur décrit de manière essentiellement « unique » l’ensemble $\mathbb N$. Plus précisément, il s’agit de montrer que si $E$ est un ensemble quelconque et $f:E\to E$ est une application qui possède les mêmes propriétés que le successeur, à savoir :
a) il existe $x\in E$ tel que $x\notin Im(f)$
b) $f$ est injective
c) si $S$ est une partie de $E$ telle que $x\in E$ et $f(y)\in S$ dès que $y\in S$, on a $S=E$, alors $(E,f)$ est « isomorphe à $\mathbb N$ », c’est-à-dire qu’il existe une bijection $g:\mathbb N\to E$ telle que $g^{-1}\circ f\circ g=s$. Cela signifie que sur le plan mathématique, $s$ et $f$ sont « indiscernables ».
i) On définit $g:\mathbb N\to E$ en posant $g(0)=x$ et pour tout $n\in\mathbb N$, $g(n+1)=f(g(n))$. Montrer que $g$ est définie sur tout l’ensemble $\mathbb N$.
ii) Soit $S=Im(g)$. En utilisant la propriété (c) de $f$, montrer que $g$ est surjective.
iii) Soit l’ensemble $S=\{n\in\mathbb N : \forall m<n,\ g(m)\neq g(n)\}$. Démontrer que $S=\mathbb N$, et en conclure que $g$ est injective. Indication : pour l’hypothèse de récurrence, distinguer les cas $m=0$ et $m>0$.
iv) Conclure en exprimant $g^{-1}\circ f\circ g$.
2.Structure opératoire de l’ensemble $\mathbb N$
2.1.Définition de l’addition
Jusqu’à maintenant, nous avons usé de descriptions intuitives des propriétés de $+$, $\times$, $<$ et $\leq$ sur les entiers naturels; seule la relation de divisibilité $|$ a été définie à partir de la multiplication dès le premier cours du semestre I. Il est possible de « réduire » toutes ces opérations et relations à la seule fonction successeur, c’est-à-dire de les définir par récurrence à partir de $s$, si bien que les trois axiomes de la section 1 déterminent toute l’arithmétique naturelle, c’est-à-dire la théorie opératoire des nombres entiers naturels. Nous allons, en d’autres termes, « construire » rigoureusement l’addition et la multiplication des entiers naturels, et ultérieurement définir l’ordre naturel à partir de l’addition, comme nous avons défini la divisibilité à partir de la multiplication. Cette approche jette une certaine lumière sur la théorie élémentaire des nombres et les relations entre les systèmes de nombres, et correspond à la philosophie générale qui consiste à « reconstruire » tous les objets mathématiques à partir des plus simples, les ensembles de nombres à partir de $\mathbb N$, les opérations à partir du successeur. Elle servira aussi d’introduction naturelle à la théorie de la récursivité, pièce essentielle de la logique mathématique et fondement historique de l’informatique, pour les étudiant(e)s qui voudront s’y intéresser. Nous commençons par l’addition.
Définition 2.1
L’addition des entiers naturels est l’unique application $+:\mathbb N^2\to \mathbb N$ possédant les propriétés suivantes, pour tous entiers naturels $m$ et $n$ :
i) $m+0=m$ (pour tout $m\in\mathbb N$, on pose $m+0:=m$)
ii) $m+s(n)=s(m+n)$ (pour tous $m,n\in\mathbb N$, si $m+n$ est défini, on pose $m+(n+1):=(m+n)+1$).
Il s’agit bien ici d’une définition par récurrence, dont le principe est appliqué comme suit : on choisit un entier naturel $m$ et on définit l’entier $m+n$ pour tout entier naturel $n$, en commençant par définir $m+0$ et en utilisant la définition de $m+n$ pour concevoir celle de $m+s(n)$. Par le théorème de récurrence 1.2, appliqué ici à l’ensemble $\mathbb N$, à l’élément $m$ et à la fonction $s$, il existe une unique application $g:\mathbb N\to\mathbb N$ telle que $g(0)=$ et $g(s(m))=s(g(m))$, et cette fonction est « l’addition de $n$ à $m$ », autrement dit on a posé $m+n:=g(n)$. Ceci signifie que pour chaque entier naturel $m$, on définit une fonction différente, qui permet de définir $m+n$ pour tout $n\in\mathbb N$. Puisque la définition est posée pour tout entier naturel $m$ « fixé » (c’est-à-dire choisi à l’avance), l’expression $m+n$ est bien définie pour tous entiers naturels $m$ et $n$. Il faut comprendre que les entiers $m$ et $n$ n’ont pas le même statut dans la définition : $m$ joue en quelque sorte le rôle de paramètre, tandis que la définition par récurrence porte sur $n$, une définition différente étant nécessaire pour chaque entier $m$. Il faudra désormais revenir à cette définition dans toute utilisation de l’addition, par exemple dans les démonstrations, ce qui permettra de bien en comprendre le principe. Les propriétés de l’addition, que nous avons auparavant considérées comme intuitives, vont en effet devenir des théorèmes, que nous allons devoir démontrer par récurrence. C’est tout l’intérêt de cette approche, qui nous permet de ramener la liste des propriétés intuitives de l’ensemble $\mathbb N$ à celles de l’axiomatique de Peano. Notons que pour tout entier naturel $n$, l’expression $n+1$ est désormais définie à partir de la définition de $+$. En effet, par définition de la fonction successeur, de $0$ et de $1$, on a $1=s(0)$; on en conclut alors que $n+1=n+s(0)=s(n+0)=s(n)$. Si donc on définit $1$ comme le successeur de $0$, $n+1$ est le successeur de $n$. Nous ne jouons pas ici sur les mots : dans les cours précédents, $n+1$ était par définition le successeur de $n$, au sens où nous avons défini de manière intuitive le successeur; à présent, l’expression reçoit son sens de la définition de l’addition. Démontrons les propriétés élémentaires de celle-ci :
Proposition 2.2
L’addition des entiers naturels possède les propriétés suivantes, pour tous entiers naturels $m,n$ et $p$ :
o) $m+0=m$
i) $(m+n)+p=m+(n+p)$ (l’addition est dite « associative »)
ii) $m+n=n+m$ (l’addition est dite « commutative »).
Démonstration
o) Cette propriété est vraie par définition.
i) Nous procédons par récurrence sur $p$, $m$ et $n$ étant donnés comme paramètres. Si $p=0$, on a $(m+n)+p=(m+n)+0=m+n$ (par définition) $=m+(n+0)$ (idem) $=m+(n+p)$, donc l’associativité est vérifiée pour $p=0$. Supposons qu’elle le soit au rang $p$, c’est-à-dire que $(m+n)+p=m+(n+p)$ : on a $(m+n)+s(p)=s((m+n)+p))$ (par définition) $=s(m+(n+p))$ (par hypothèse de récurrence) $=m+s(n+p)$ (par définition) $=m+(n+s(p))$ (par définition), ce qui est l’associativité au rang $p+1$, donc la propriété est vérifiée pour tout $p\in\mathbb N$ par récurrence. Comme $m$ et $n$ sont arbitraires, elle est vérifiée pour tous $m,n,p\in\mathbb N$.
ii) Nous procédons par récurrence sur $n$, $m$ étant choisi comme paramètre. Si $n=0$, on a $m+n=m+0=m$ par définition : nous voulons montrer que $m=0+m$, ce qui n’est pas dans la définition, donc nous introduisons un second argument par récurrence, à l’intérieur du premier, et portant cette fois-ci sur $m$. Si $m=0$, on a $m=0=0+0$ (par définition) $=0+m$, donc la propriété est vérifiée pour $m=0$. Supposons qu’elle le soit au rang $m$, c’est-à-dire que $m=0+m$ : on a $s(m)=s(0+m)$ (par hypothèse de récurrence dans le second argument) $=0+s(m)$ (par définition) donc la propriété est vraie pour tout $m$ par récurrence, ce qui clôt le second argument. On montrerait aussi par une autre récurrence auxiliaire que pour tout $m\in\mathbb N$, on a $m+1=1+m$. Revenant à notre argument principal, nous avons montré que $m+0=m=0+m$ pour tout $m\in\mathbb N$, donc la propriété (ii) est valide au rang $n=0$. Supposons qu’elle le soit au rang $n$, c’est-à-dire que $m+n=n+m$ pour $m$ choisi d’avance; on obtient $m+(n+1)=m+s(n)=s(m+n)$ (par définition) $=s(n+m)$ (par hypothèse de récurrence) $=n+s(m)$ (par définition) $=n+(m+1)=n+(1+m)$ (par ce qui précède) $=(n+1)+m$ (par (i)), donc $m+(n+1)=(n+1)+m$, ce qui est la propriété au rang $n+1$, et par récurrence on conclut que (ii) est vraie pour tout $n\in\mathbb N$, et comme $m$ a été choisi de manière arbitraire, pour tous $m,n\in\mathbb N$. $\square$
Remarque 2.3
Dans le principe de récurrence (axiome 3), on passe de l’étape $n$ à l’étape $s(n)$. Dans les raisonnements par récurrence introduits dans le premier cours, on passe du rang $n$ au rang $n+1$. Ceci n’introduit pas d’ambiguïté puisque nous avons identifié $n+1$ et $s(n)$ par définition de l’addition. Nous utilisons les deux notations selon le contexte.
La figure suivante représente l’étape de récurrence dans la définition de l’addition à partir de la fonction successeur.
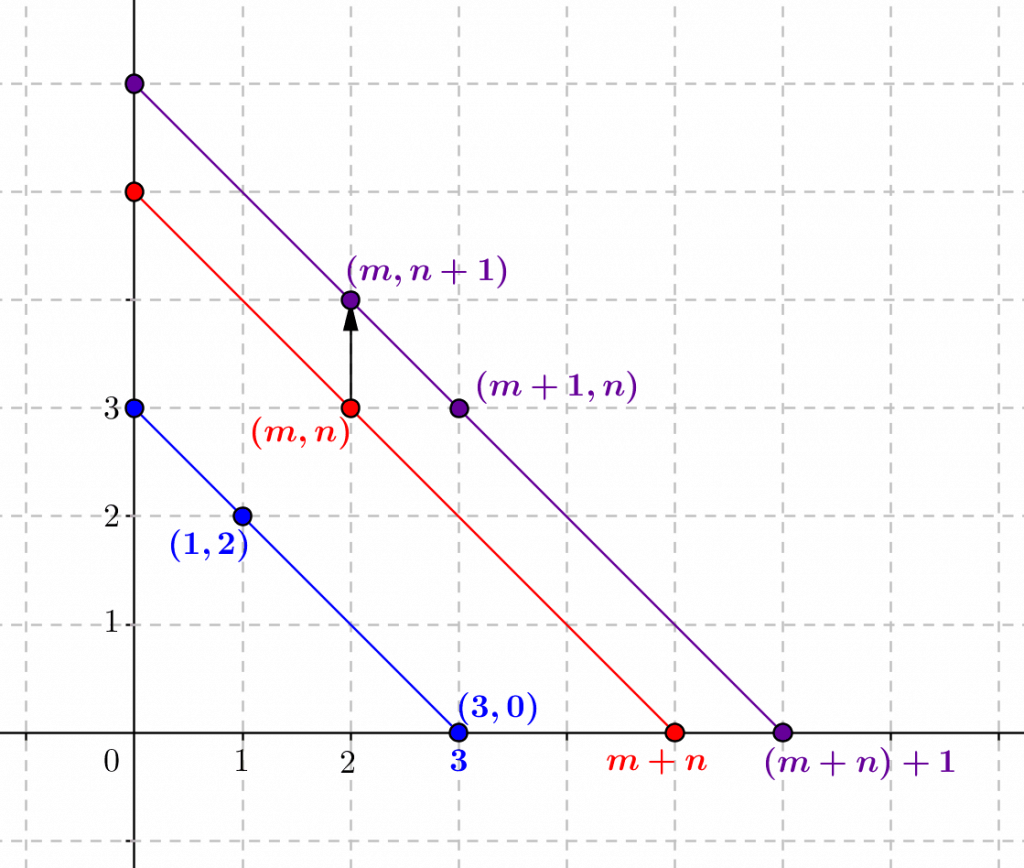
+1)$ à partir de $m+n$ apparaît en passant verticalement du point $(m,n)$ au point $(m,n+1)$, qui se trouve sur la diagonale « suivante ». Les points $(m,n+1)$ et $(m+1,n)$ sont sur la même diagonale, illustrant que $(m+n)+1=(m+1)+n$.
2.2.Définition de la multiplication
Nous poursuivons la « réduction » des opérations usuelles de l’ensemble $\mathbb N$ à la fonction successeur, en utilisant l’addition pour définir la multiplication, de nouveau par récurrence. Le procédé est analogue à ce que nous avons fait pour l’addition :
Définition 2.4
L’addition des entiers naturels est l’unique application $+:\mathbb N^2\to \mathbb N$ possédant les propriétés suivantes, pour tous entiers naturels $m$ et $n$ :%et $p$ :
i) $m+0=m$ (pour tout $m\in\mathbb N$, on pose $m+0:=m$)
ii) $m+s(n)=s(m+n)$ (pour tous $m,n\in\mathbb N$, si $m+n$ est défini, on pose $m+(n+1):=(m+n)+1$).
Définition 2.5
La multiplication (des entiers naturels) est l’unique application $\times:\mathbb N^2\to \mathbb N$ possédant les propriétés suivantes, pour tous entiers naturels $m$ et $n$ : i) $m\times 0=0$ (pour tout $m\in\mathbb N$, on pose $m\times 0:=0$) ii) $m\times s(n)=(m\times n)+m$ (pour tous $m,n\in\mathbb N$, si $m\times n$ est défini, on pose $m\times (n+1):=(m\times n)+m$).
Comme dans la définition de l’addition, nous définissons le produit $m\times n$, par récurrence sur $n$, pour tout entier naturel $m$ séparément : il y a autant de définitions par récurrence que d’entiers $m\in\mathbb N$. Dans cette définition, nous utilisons d’ailleurs l’addition telle qu’elle est désormais définie par récurrence. Nous noterons indifféremment $m\times n$, $m.n$ ou $mn$ le produit de deux entiers naturels $m$ et $n$. A partir de cette définition, les propriétés admises auparavant de manière intuitive pour la multiplication peuvent désormais être démontrées par récurrence.
Proposition 2.6
La multiplication des entiers naturels possède les propriétés suivantes, pour tous entiers naturels $m,n$ et $p$ :
o) $m.1=m$
i) $(m+n).p=(m.p)+(n.p)$ et $p.(m+n)=p.m+p.n$ (la multiplication est distributive sur l’addition)
ii) $m.n=n.m$ (la multiplication est commutative)
iii) $(m.n).p=m.(n.p)$ (la multiplication est associative).
Démonstration
Nous démontrons ces propriétés en utilisant notamment les propriétés de l’addition démontrées dans la proposition 2.2.
o) On a $m.1=m.s(0)=m.0+m$ (par définition de $\times$) $=0+m$ (par définition de $\times$ à nouveau) $=m$, par les propriétés de l’addition.
i) Nous procédons par récurrence sur $p$. Si $p=0$, on a $(m+n).0=0$ (par définition) $=(m.0)+(n.0)$ (par définition et par les propriétés de l’addition), donc la propriété est vérifiée au rang $p=0$. Supposons qu’elle le soit au rang $p\geq 0$, c’est-à-dire que $(m+n).p=(m.p)+(n.p)$; on obtient $(m+n).s(p)=(m+n).p+(m+n)$ (par définition) $=(m.p)+(n.p)+m+n$ (par hypothèse de récurrence) $=(m.p+m)+(n.p+n)$ (par associativité de $+$) $=m.s(p)+n.s(p)$ (par définition), ce qui est la propriété au rang $s(p)=p+1$, et l’énoncé est démontré pour tout $p\in\mathbb N$ par récurrence. On démontrerait de même que $p.(m+n)=p.m+p.n$.
ii) Nous montrons d’abord que pour tout $n\in\mathbb N$, on a $0.n=0$. Pour $n=0$, c’est vrai par définition. Si c’est vrai au rang $n$, on a $0.s(n)=0.n+0$ (par définition) $=0.0$ (par hypothèse de récurrence) $=0$, donc la propriété est vraie au rang $s(n)$ et elle est donc vraie pour tout $n$ par récurrence. Nous montrons ensuite que pour tout $m\in\mathbb N$, on a $m.1=m=1.m$. Si $m=0$, on a $m.1=0.1=1.0$ (par ce qui précède) $=1.m$. Si la propriété est vérifiée pour $m$, on a $(m+1).1=m.1+1.1$ (par (i)) $=m.1+1$ (par (o)) $=1.m+1$ (par hypothèse de récurrence) $=1.(m+1)$, donc la propriété est vérifiée pour tout $m\in\mathbb N$ par récurrence. On montre alors la propriété générale par récurrence sur $n$, $m$ étant un entier naturel quelconque choisi. Si $n=0$, on a $m.0=0.m=0$ par ce qui précède, donc la propriété est vérifiée au rang $n=0$. Supposons qu’elle le soit au rang $n\in\mathbb N$, c’est-à-dire que $m.n=n.m$ : on obtient $m.(n+1)=m.n+m$ (par définition) $=n.m+m$ (par hypothèse de récurrence) $=(n+1).m$ (par (o), (i) et ce qui précède) $=s(n).m$, donc la propriété est valide au rang $n+1$, et par récurrence elle l’est pour tout $n\in\mathbb N$, et donc pour tous $m,n\in\mathbb N$, puisque $m$ a été choisi arbitrairement.
iii) Nous procédons à nouveau par récurrence sur $p$, $m$ et $n$ ayant été choisis arbitrairement. On a $(m.n).0=0=m.0=m.(n.0)$ par définition, donc la propriété est vérifiée pour $p=0$. Si elle l’est pour $p$, autrement dit si on a $(m.n).p=m.(n.p)$, on obtient $(m.n).s(p)=(m.n).p+m.n$ (par définition) $=m.(n.p)+m.n$ (par hypothèse de récurrence) $=m.(n.p+n)$ (par (i) et (ii)) $=m.(n.s(p))$ (par définition); c’est la propriété au rang $p+1$, donc par récurrence la propriété est vérifiée pour tout $p\in\mathbb N$, et donc pour tous $m,n,p\in\mathbb N$. $\square$
Remarque 2.7
Rappelons que lorsque nous démontrons par récurrence des propriétés dépendant de plusieurs entiers naturels, il arrive souvent que la récurrence porte sur l’un d’entre eux seulement, les autres étant « fixés », c’est-à-dire choisis arbitrairement mais déterminés. Par exemple, si la propriété $P(m,n,p)$ dépend de trois entiers, on veut montrer que l’ensemble des triplets $(m,n,p)$ pour lesquels $P(m,n,p)$ est vraie est l’ensemble $\mathbb N^3$ tout entier. Pour cela, on peut se ramener à montrer que si $m$ et $n$ quelconques sont donnés, $\{p\in\mathbb N : P(m,n,p)\}$ est $\mathbb N$ tout entier.
En outre, la multiplication possède la propriété dite « d’intégrité » suivante :
Proposition 2.8
Si $m$ et $n$ sont deux entiers naturels tels que $m.n=0$, alors $m=0$ ou $n=0$.
Démonstration
Supposons que $m\neq 0$ et $n\neq 0$ : par la proposition 1.1, il existe $p,q\in\mathbb N$ tels que $m=p+1$ et $n=q+1$, d’où $m.n=(p+1).(q+1)=p.q+p+q+1$, nombre différent de $0$ par l’axiome 1, car successeur de $p.q+p+q$. Par contraposée, si $m.n=0$, alors $m=0$ ou $n=0$. $\square$
La figure suivante représente l’étape de récurrence dans la définition de la multiplication à partir de l’addition et du successeur.

2.3.Exercices de la section
Exercice 2.9
i) (Subtil) Démontrer que l’addition, définie à partir du successeur, est l’addition dont on a admis l’existence et les propriétés de manière intuitive, autrement dit, qu’il n’existe qu’une seule application $A:\mathbb N\times\mathbb N\to\mathbb N$ qui possède les propriétés de la proposition 2.2.
ii) Compléter la démonstration de la proposition 2.2 en montrant que pour tout entier naturel $m$, on a $m+1=1+m$.
iii) Démontrer que pour tous entiers naturels $m,n$ et $p$, on a $m.(p+n)=m.p+m.n$, sans utiliser les clauses (ii) et (iii) de la proposition 2.6.
iv) Soit $f:\mathbb N\times\mathbb N\to \mathbb N$ une application telle que pour tous $m,n\in\mathbb N$, on a $f(m,0)=0$ et $f(m,n+1)=f(m,n)+f(m)$. Montrer par récurrence que l’application $f$ est la multiplication.
v) Par définition, on a $2=s(1)$, $3=s(2)$, $4=s(3)$, et ainsi de suite. Démontrer que $2+2=4$, $2\times 2=4$, $2+3=5$ et $2\times 3=6$.
3.Les relations d’ordre naturel et de divisibilité
3.1.L’addition et l’ordre naturel
Dans le premier cours, nous avons adopté une compréhension intuitive de l’addition et de l’ordre naturel. En nous servant des relations intuitives entre les deux, nous pouvons désormais définir le second à partir de la première. La propriété suivante de l’addition, appelée « simplifiabilité », est fondamentale et nous sera utile pour établir les propriétés de l’ordre naturel.
Lemme 3.1
Soient $m,n$ et $p$ trois entiers naturels.
i) Si $m+n=m+p$, alors on a $n=p$ (l’addition dans $\mathbb N$ est « simplifiable »).
ii) Si $m,n\in\mathbb N$ et $m+n=0$, alors $m=n=0$.
Démonstration
i) On se donne $n$ et $p$ quelconques, et on procède par récurrence sur $m$. Supposons que $m=0$ : si $m+n=m+p$, c’est que $n=0+n=0+p=p$ et la propriété est trivialement vraie dans ce cas. Supposons qu’elle le soit à un rang $m$, c’est-à-dire que l’énoncé « $\forall n,p\in\mathbb N,\ m+n=m+p\Rightarrow n=p »$ soit vrai; si maintenant $(m+1)+n=(m+1)+p$, par associativité de l’addition on a $m+(1+n)=m+(1+p)$ et par hypothèse de récurrence appliquée à $1+n$ et $1+p$, on a $1+n=1+p$, soit $n+1=p+1$ par commutativité de l’addition (proposition 2.2). Deux nombres ayant le même successeur sont égaux (par l’injectivité de $s$, axiome 2 de Peano), donc $n=p$, la propriété est vérifiée au rang $m+1$, et par récurrence elle est vraie pour tout $m\in\mathbb N$, et donc pour tous $m,n,p\in\mathbb N$.
ii) Supposons par l’absurde que $m+n=0$ mais que l’un des nombres $m$ ou $n$ n’est pas nul, par exemple $m$ (l’autre cas se traite de manière similaire par commutativité de l’addition). Par la proposition 1.1, $m$ est le successeur d’un entier naturel $p$, c’est-à-dire $m=p+1$. On obtient $0=m+n=(p+1)+n=(p+n)+1$, par associativité et commutativité de l’addition; en particulier, $0$ est le successeur de $p+n$, ce qui contredit l’axiome 1. Par reductio ad absurdum, on en conclut que $m=n=0$. $\square$
Souvenons-nous de la relation intuitive entre l’addition des entiers naturels et la relation d’inégalité large sur $\mathbb N$ : pour tous entiers naturels $m$ et $n$, on a $m\leq n$ si et seulement si il existe un entier naturel $p$ tel que $m+p=n$. Puisque nous avons défini l’addition à partir du successeur, nous allons désormais utiliser cette propriété pour définir la relation $\leq$ à partir de l’addition.
Définition 3.2
Si $m$ et $n$ sont deux entiers naturels, nous dirons que $m$ est inférieur ou égal à $n$, ce que nous notons $m\leq n$, si il existe un entier naturel $p$ tel que $m+p=n$. La relation binaire $(\mathbb N,\mathbb N,\leq)$ est appelée ordre large sur les entiers naturels.
Remarque 3.3
Insistons : ici, nous « oublions » volontairement l’approche intuitive de la relation $\leq$, de même que nous avons oublié dans la section précédente l’approche intuitive de l’addition et de la multiplication. Nous « reconstituons » tout à partir du successeur.
Exemple 3.4
Le nombre $2$ est inférieur au nombre $5$, parce qu’il existe un entier naturel $n=3$, tel que $2+3=5$. En revanche, $2$ n’est pas inférieur à $1$, parce que pour aucun entier naturel $n$ on n’a $1=2+n$ (sinon, par le lemme 3.1 on a aurait $0=n+1$, ce qui contredirait l’axiome 1).
On peut exprimer symboliquement cette définition en disant que la relation $\leq$ est définie comme la relation binaire sur $\mathbb N$, de graphe $R=\{(m,n)\in\mathbb N^2 : \exists p\in\mathbb N,\ n=m+p\}$.
La relation $\leq$ étant à présent définie à partir de l’addition, ses propriétés é\-lé\-men\-tai\-res, admises de manière intuitive dans les premier cours, sont maintenant retrouvées comme conséquences des propriétés de l’addition :
Proposition 3.5
Soient $m,n$ et $p$ des entiers naturels. On a les propriétés suivantes :
o) $0\leq m$ ($0$ est le plus petit entier naturel)
i) $m\leq m$ (la relation $\leq$ est dite « réflexive »)
ii) si $m\leq n$ et $n\leq p$, alors $m\leq p$ (la relation $\leq$ est dite « transitive »)
iii) si $m\leq n$ et $n\leq m$, alors $m=n$ (la relation $\leq$ est dite « anti-symétrique »)
iv) si $m\leq n$, alors $m+p\leq n+p$ (la relation $\leq$ est « compatible » à l’addition).
v) Si $m\leq n$, alors $m\times p \leq n\times p$ (la relation $\leq$ est « compatible » à la multiplication).
Démonstration
o) Par la proposition 2.2, on a $0+m=m$, donc par définition de $\leq$ on obtient $0\leq m$. i) Par définition de $+$, on a $m+0=m$, donc par définition de $\leq$ on a $m\leq m$. ii) Si $m\leq n$ et $n\leq p$, par définition de $\leq$ il existe $q,r\in\mathbb N$ tels que $n=m+q$ et $p=n+r$, d’où $p=n+r=(m+q)+r=m+(q+r)$ par associativité de l’addition, et par définition de $\leq$, ceci signifie que $m\leq p$. iii) Supposons que $m\leq n$ et $n\leq m$, c’est-à-dire qu’il existe $p,q\in\mathbb N$ tels que $n=m+p$ et $m=n+q$ : on obtient $n=m+p=(n+q)+p=n+(q+p)$ (par associativité de l’addition). Par le lemme 3.1 (clause (i)), on en déduit que $0=p+q$, et par la clause (ii) du même lemme que $p=q=0$, d’où $m=n+q=n+0=n$. iv) Supposons que $m\leq n$ : il existe $q\in\mathbb N$ tel que $n=m+q$, d’où $n+p=(m+q)+p=m+(q+p)=m+(p+q)=(m+p)+q$, c’est-à-dire $m+p\leq n+p$. v) Si $m\leq n$, c’est qu’il existe un entier naturel $k$ tel que $m+k=n$ : on a alors $m.p+k.p=(m+k)\times p=n.p$ par les propriétés de la multiplication 2.6. Par définition de $\leq$, on a $m.p\leq n.p$. $\square$
A partir de la relation d’ordre large $\leq$, nous pouvons désormais définir la relation d’ordre « strict » $<$, dit aussi « ordre linéaire », en posant, pour $m,n\in\mathbb N$, $m<n$ si et seulement $m\leq n$ et $m\neq n$. La propriété suivante est alors une conséquence directe de la définition de $\leq $ :
Proposition 3.6
Pour tous entiers naturels $m$ et $n$, on a $m<n$ si et seulement si il existe $p\in\mathbb N^*$, tel que $n=m+p$.
Démonstration
Supposons d’abord que $m<n$ : en particulier, on a $m\leq n$ donc il existe $p\in\mathbb N$, tel que $n=m+p$. Supposons par l’absurde que $p=0$ : on a alors $n=m+p=m+0=m$, ce qui contredit le fait que $m\neq n$; par reductio ad absurdum, on en déduit que $p\neq 0$. Réciproquement, supposons qu’il existe $p\neq 0$ tel que $n=m+p$ : on a donc $m\leq n$, et par la contraposée de la clause (i) du lemme 3.1, on a $m+0\neq m+p$, c’est-à-dire $m\neq n$, d’où finalement $m<n$. $\square$
Exemple 3.7
On a $11<17$, parce qu’il existe un entier naturel non nul $n=6$ tel que $11+n=17$. En revanche, on n’a pas $5<5$, parce qu’il n’existe pas d’entier naturel $n>0$ tel que $5+n=5$ (sinon, $n$ serait de la forme $m+1$ par la proposition 1.1, d’où $5=5+(m+1)$ et donc $0=m+1$ par le lemme 3.1, ce qui contredirait à nouveau l’axiome 1).
La figure suivante représente les relations d’ordre large $\leq$ et d’ordre strict $<$ sur les entiers naturels, à partir de leur représentation sur les nombres réels.
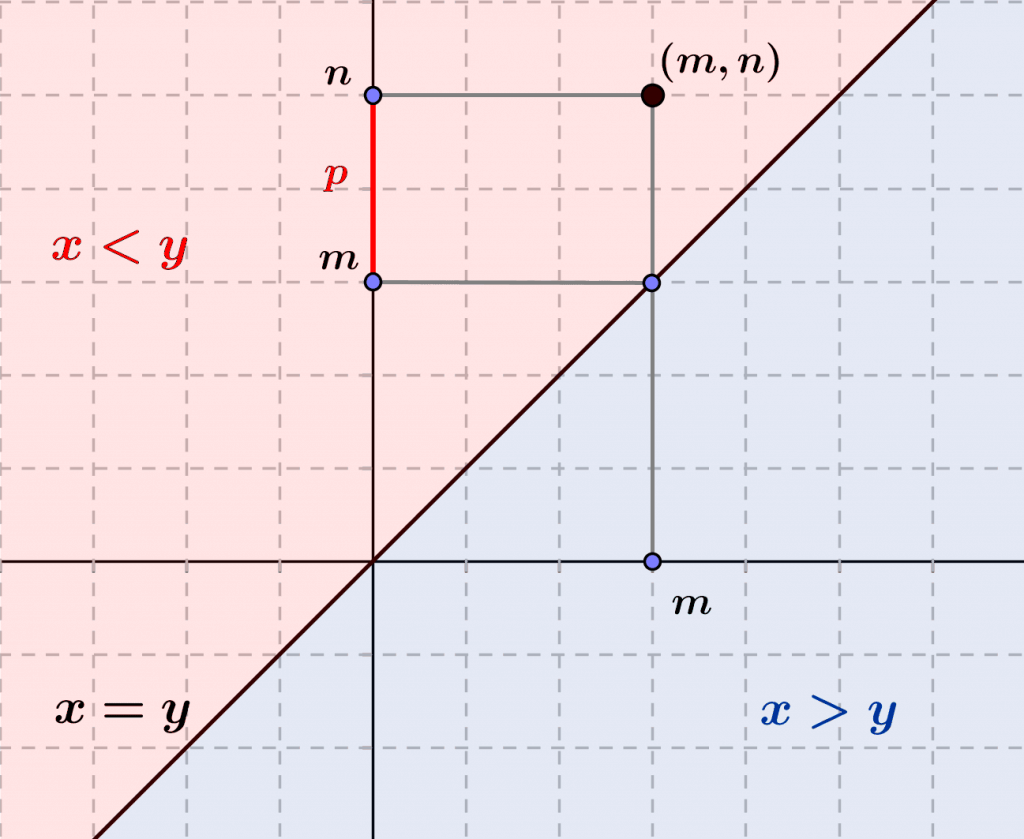
Cette caractérisation « intrinsèque » de la relation $<$ à partir de l’addition ne mentionne plus la relation $\leq$ à partir de laquelle on l’a définie. Ceci signifie que nous aurions pu définir directement la relation $<$ à partir de $+$, et nous en aurions alors déduit que $m < n\Leftrightarrow (m\leq n\ \wedge\ m\neq n)$, ou nous aurions même pu définir $\leq$ à partir de $<$ en posant, pour tous entiers naturels $m,n$, $m\leq n$ si et seulement si $m<n$ ou $m=n$.
Les propriétés usuelles de $<$ sont reprises dans les exercices. L’important est ici de retenir la propriété de trichotomie de l’ordre linéaire :
Proposition 3.8
Soient $m$ et $n$ deux entiers naturels. L’un des cas suivants est toujours vérifié, à l’exclusion des deux autres : i) $m<n$ ii) $m=n$ iii) $m>n$.
Démonstration
Distinguons deux cas, selon qu’il existe $p\in\mathbb N$ tel que $n=m+p$ (c’est-à-dire $m\leq n$) ou non. Si un tel $p$ existe, alors soit $p\neq 0$ et $m<n$ par la proposition 3.6, soit $p=0$ et alors $m=n$. Ces deux sous-cas sont évidemment mutuellement exclusifs. Dans le second cas, il n’existe pas d’entier naturel $p$ tel que $n=m+p$. Démontrons par récurrence sur $n$ que l’on a alors $n<m$; remarquons qu’on a toujours $n\neq m$, sinon on se trouve dans le premier cas. Si $n=0$, alors on a $m=0+m=n+m$, d’où $n\leq m$, et donc $n<m$. Supposons que la propriété est vérifiée au rang $n$, c’est-à-dire que si on n’a pas $m\leq n$, alors $n<m$, et supposons qu’on n’a pas $m\leq n+1$. En particulier, on n’a pas $m\leq n$, sinon il existerait $p\in\mathbb N$ tel que $n=m+p$, d’où $n+1=m+(p+1)$, et on aurait $m\leq n+1$. Par hypothèse de récurrence, on a donc $n<m$, donc il existe par la proposition 3.6 un entier naturel $p\neq 0$ tel que $n+p=m$. Par la proposition 1.1, $p$ est de la forme $s(q)=q+1$, si bien que $n+p=n+(q+1)=(n+1)+q=m$, d’où $n+1\leq m$. Comme $m\neq n+1$, par le principe de récurrence, la propriété est démontrée au rang $n+1$, si bien que le second cas est démontré et comme il est incompatible avec le premier, la démonstration est terminée. $\square$
Remarque 3.9
Dans le second cas, on montre que si $m,n\in\mathbb N$ et $\neg (m\leq n)$, alors $n<m$. La démonstration se fait par récurrence, de la manière suivante : on considère $m$ comme « paramètre », c’est-à-dire un entier donné, et on mon
3.2.Minimum et maximum
De la proposition 3.8, il découle que l’ordre $\leq$ est un ordre total, autrement dit que pour tous $m,n\in\mathbb N$, on a soit $m\leq n$, soit $n\leq m$.
En particulier, il existe toujours un maximum et un minimum pour deux tels éléments, au sens de la définition suivante :
Définition 3.10
Soient $n$ et $m$ deux entiers naturels.
i) Le minimum de $n$ et $m$ est le plus petit des entiers $n$ et $m$, soit $n$ si $n\leq m$, ou $m$ si $m\leq n$. On le note $\min\{n,m\}$.
ii) Le maximum de $n$ et $m$ est le plus grand des entiers $n$ et $m$, soit $m$ si $n\leq m$, ou $n$ si $m\leq n$. On le note $\max\{n,m\}$.
Les propriétés naturelles de $\min$ et de $\max$ sont les suivantes :
Proposition 3.11
Si $m,n$ et $p$ sont trois entiers naturels, on a :
i) $m=n$ si et seulement si $\min\{n,m\}=\max\{n,m\}$
ii) $m\leq n$ si et seulement $\min\{n,m\}=m$, si et seulement $\max\{n,m\}=n$
iii) $m+\min\{n,p\}=\min\{m+n,m+p\}$ et $m+\max\{n,p\}=\max\{m+n,m+p\}$
iv) $m\times\min\{n,p\}=\min\{m\times n,m\times p\}$ et $m\times\max\{n,p\}=\max\{m\times n,m\times p\}$.
Démonstration
La démonstration de (i) à (iii) est laissée en exercice à l’étudiant(e) (voir les exercices de la section). Démontrons (iv) en distinguant deux cas, selon que $n\leq p$ ou $p\leq n$. Si $n\leq p$, alors $\min\{n,p\}=n$, donc $m\times \min\{n,p\}=m\times n$; comme aussi $m\times n\leq m\times p$ par la proposition 3.5(v), on a $\min\{m\times n,m\times p\}=m\times n$, d’où la première égalité dans ce cas. Si $p\neq n$, en échangeant les rôles de $n$ et $p$ dans le premier cas, on obtient aussi la première égalité. La seconde égalité se démontre de manière parfaitement analogue. $\square$
Exemple 3.12
Le minimum de $15$ et $9$ est $9$, puisque $9<15$ et pour la même raison, le maximum de $9$ et $15$ est $15$. On vérifie bien qu’on a $\min\{20,31\}=11+\min\{9,15\}=20$, et qu’on a $\max\{63,105\}=\max\{9.7,15.7\}=7\times\max\{9,15\}=7.15=105$.
3.3.La multiplication et la divisibilité
Notre définition de la relation d’ordre large $\leq$ à partir de l’addition était l’analogie parfaite de celle que nous avons donnée dès le premier cours, de la relation de divisibilité $|$ à partir de la multiplication. Nous avons en effet décrété que pour tous $m,n\in\mathbb N$, $m$ divise $n$ si et seulement si il existe $d\in \mathbb N$ tel que $n=m.d$, symboliquement : $m|n\Leftrightarrow \exists d\in\mathbb N,\ m.d=n$.
Cette définition étant parfaitement rigoureuse, elle s’intègre à notre description de $\mathbb N$ à partir de l’arithmétique de Peano. L’arithmétique « naturelle », à proprement parler, est l’étude de la relation de divisibilité dans l’ensemble $\mathbb N$, que nous entreprendrons dans la suite du chapitre et poursuivrons par l’arithmétique élémentaire dans l’ensemble $\mathbb Z$ au chapitre suivant. Pour l’heure, nous énonçons les propriétés élémentaires de $|$, analogues à celles de $\leq$, qui proviennent directement des propriétés de $\times$.
Définition 3.13
Si $m$ et $n$ sont deux entiers naturels tels que $m|n$, on dit que $n$ est un multiple de $n$ et que $m$ est un diviseur de $n$.
Exemple 3.14
Le nombre $1031$ est un multiple de $7$ et un multiple de $11$, puisqu’il existe $d=143$ tel que $1031=d\times 7$, et $k=91$ tel que $1031=k\times 11$. En revanche, le nombre $14$ n’est pas un diviseur de $128$, car sinon il existerait $k\in\mathbb N$ tel que $14.k=128$ : on aurait nécessairement $k\leq 9$ (puisque si $k>9$, on a $k\geq 10$, donc $14.k\geq 140>128$ par la proposition 3.5(v)) mais pour $k\leq 9$ on a $14.k\leq 126$ par la même proposition.
Proposition 3.15
Soient $m,n,p\in\mathbb N$. On a les propriétés suivantes : o) $1|m$ ($1$ est le « diviseur universel ») et $m|0$ ($0$ est le « multiple universel ») i) $m|m$ (la relation $|$ est réflexive) ii) si $m|n$ et $n|p$, alors $m|p$ (la relation $|$ est transitive) iii) si $m|n$ et $n|m$, alors $m=n$ (la relation $|$ est anti-symétrique).
Démonstration
Laissée comme un exercice pour l’étudiant(e) (imiter la preuve de la proposition analogue pour $\leq$). $\square$
Notons pour terminer les propriétés suivantes de « compatibilité de l’ordre strict à la multiplication », la seconde étant analogue à la proposition 2.8.
Proposition 3.16
Pour tous entiers naturels $m,n$ et $p$ :
i) si $m<n$ et $p\neq 0$, on a $m.p<n.p$
ii) si $m.p=n.p$ et $p>0$, on a $m=n$.
Démonstration
i) La démonstration est laissée en exercice à partir de la proposition 3.5.
ii) Supposons que $m\neq n$ : par la proposition 3.8, on a $m<n$ ou $n<m$; par (ii), dans les deux cas on a $m.p\neq n.p$, d’où le résultat par contraposée. $\square$
3.4.Exercices de la section
Exercice 3.17
i) Montrer que pour tous entiers naturels $m$ et $n$, on a $m<n$ si et seulement si il existe $p\in\mathbb N$ tel que $n=m+p+1$. En déduire que $m<n$ si et seulement si $m+1\leq n$.
ii) Démontrer les propriétés suivantes :
– pour tout $m\in \mathbb N$, on a $0<m+1$
– pour tout $m\in\mathbb N$, on n’a jamais $m<m$
– pour tous $m,n,p\in\mathbb N$ tels que $m<n$ et $n<p$, on a $m<p$
– pour tous $m,n,p\in\mathbb N$ tels que $m<n$, on a $m+p<n+p$.
iii) Démontrer la proposition 3.11.
iv) Démontrer les propriétés de la proposition 3.15.
v) Montrer que si $n,m\in\mathbb N$, $m\neq 0$ et $n|m$, alors $n\leq m$.
vi) Démontrer la clause (i) de la proposition 3.16.
vii) Démontrer que pour tout entier naturel $n$, on a $n<s(n)$. En déduire que $2<4$. Indication : par définition, $2=s(1)$.
Problème 3.18 [plus difficile]
Le sujet de ce problème est de donner une définition rigoureuse de $\leq$ (ou de $<$) qui ne dépend pas de l’addition; il s’agit de la définition de Bertrand Russell dans Introduction to mathematical philosophy. Nous allons pour cela caractériser l’ordre $\leq$ tel qu’il est défini ici par cette propriété alternative.
Une propriété $P$ des entiers naturels est dit héréditaire si elle est vraie pour un entier naturel $n+1$ (c’est-à-dire $s(n)$) dès qu’elle l’est pour un entier naturel $n$, autrement dit, si l’énoncé « $\forall n,\ P(n)\Rightarrow P(n+1)$ » est vrai. Nous proposons alors de démontrer que $m\leq n$ si et seulement si $n$ possède toute propriété héréditaire que possède $m$.
i) Soit $m\in\mathbb N$. Montrer que la propriété $P(k)$ définie par \og$\exists p\in\mathbb N, \ m+p=k$ », où $m$ est considéré comme un paramètre, est héréditaire.
ii) En déduire que si $n\in\mathbb N $ possède toute propriété héréditaire que possède $m$, alors $m\leq n$.
iii) Supposons que $m\leq n$, et soit $p\in\mathbb N$ tel que $m+p=n$. Montrer par récurrence sur $p$ que si $P$ est une propriété héréditaire que possède $m$, alors $n$ possède cette propriété. Conclure.
iv) Montrer que $m<n$ si et seulement si $s(n)$ possède toute propriété héréditaire que possède $m$.
[/mepr-show]
4.Divisibilité et division euclidienne
A l’école primaire, nous apprenons à diviser un entier naturel $a$ par un autre entier naturel $b$ non nul : le résultat est donné en général sous la forme d’un quotient $q$ et d’un reste $r$ sous la forme $a=b\times q+r$ avec $r<b$, et $r$ est nul exactement lorsque $a$ est divisible par $b$. En revanche, lorsque $r\neq 0$ la division euclidienne ne donne qu’une approximation de la division de $a$ par $b$.
L’interprétation intuitive de la division euclidienne, sur le plan des quantités, est la suivante : combien de fois $b$ est-il « contenu » dans $a$ ? Ou encore : étant donnée une collection de $a$ objets, quel est le nombre maximal $q$ de « paquets » de $b$ objets qu’on peut faire avec ceux-ci ? Ce nombre est maximal exactement lorsque, une fois les « paquets » rassemblés, les objets restant éventuellement ne permettent pas de former un nouveau paquet, leur nombre $r$ étant donc strictement inférieur à $b$.
Nous reconstruisons ici la théorie de la division euclidienne en utilisant nos nouveaux concepts mathématiques et les axiomes du successeur dans $\mathbb N$, et nous lui donnons ainsi un fondement numérique solide qui ne dépend plus de l’intuition des ensembles $\mathbb Z,\mathbb Q$ et $\mathbb R$ comme dans le Livre 1 (Entrer dans l’univers mathématique).
Nous pouvons traduire l’interprétation précédente sur le plan de la théorie des ensembles finis comme suit : combien d’ensembles deux-à-deux disjoints de $b$ éléments pouvons-nous former avec un ensemble de $a$ éléments ? Si $a$ est un multiple de $b$, disons $a=b.d$, alors la réponse est $d$, bien sûr, mais en général $a$ n’est pas divisible par $b$, donc il nous faut obtenir la « meilleure approximation ».
Nous aurons pour ceci besoin de résultats auxiliaires sur le « plus grand élément » et le « plus petit élément » de certains sous-ensembles de $\mathbb N$ (on pourra se reporter au cours \no 2 pour la théorie des ensembles finis et de leur cardinal).
Lemme 4.1
Tout sous-ensemble fini $S$ non vide de $\mathbb N$ possède un plus grand élément, autrement dit il existe $n\in S$ tel que pour tout $m\in S$, on ait $m\leq n$.
Démonstration
On procède par récurrence sur le cardinal $k$ de $S$. Si $k=1$, alors $S$ ne possède qu’un élément $n$, qui est nécessairement le plus grand élément de $S$. Supposons que la propriété est vérifiée pour les sous-ensembles finis de cardinal $k>1$, et que $|S|=k+1$. Soit $i\in S$ un élément quelconque : l’ensemble $S-\{i\}$ est fini et possède $k$ éléments (Cours \no 3, chapitre 2), donc par hypothèse de récurrence il possède un plus grand élément, appelons-le $m$. Soit alors $n$ le plus grand des deux nombres $i$ et $m$, par la proposition 3.8, et soit $j\in S$ : si $j=i$, alors on a $j\leq n$, tandis que si $j\neq i$, par définition de $m$ on a $j\leq m\leq n$. Il s’ensuit que $n$ est le plus grand élément de $S$, et le lemme est démontré par récurrence. $\square$
Exemple 4.2
L’ensemble $2\mathbb N$ des entiers naturels pairs (c’est-à-dire multiples de $2$) est infini, donc il ne possède pas de plus grand élément (par contraposée du lemme 4.1). En effet, si $n\in 2\mathbb N$, $n$ est de la forme $2.m$ pour $m\in\mathbb N$, et on a $n=2.m.<2.(m+1)\in 2\mathbb N$.
Proposition 4.3
Tout sous-ensemble non vide $S$ de $\mathbb N$ possède un plus petit élément, autrement dit il existe $n\in S$ tel que pour tout $m\in S$, on a $n\leq m$.
Démonstration
Distinguons deux cas. Dans le premier, si $0\in S$ alors $0$ est évidemment le plus petit élément de $S$. Dans le second, on suppose que $0\notin S$, et on considère alors l’ensemble $X$ de tous les entiers naturels qui sont strictement plus petits que tous les éléments de $S$, c’est-à-dire $X=\{i\in \mathbb N : \forall m\in S,\ i< m\}$. Par hypothèse, $X$ n’est pas vide, puisque $0\in X$. Comme $S$ n’est pas vide non plus, il existe $a\in S$, si bien que $X\subseteq [[0,a]]=\{n\in\mathbb N : n\leq a\}$, donc $X$ est fini comme sous-ensemble d’un ensemble fini (C1.II.3, Corollaire 2.1). Par le lemme 4.1, $X$ possède un plus grand élément, notons-le $k$. Par définition de $X$ et de $k$, pour tout $m\in S$ on a donc $k<m$, soit, par l’exercice 3.17(i)], $k+1\leq m$. Comme $k+1\in S$, il s’ensuit que $k+1$ est le plus petit élément de $S$. $\square$
Remarque 4.4
Cette propriété de l’ordre naturel sur $\mathbb N$ concerne tous les sous-ensembles de $\mathbb N$, et est à la base de la représentation de $\mathbb N$, avec la relation $<$, comme un ordinal, c’est-à-dire la version formelle d’un nombre infini conçu comme un « type d’ordre ». La proposition 4.3 est en fait équivalente au principe de récurrence (voir les exercices).
Théorème 4.5 [Division euclidienne]
Si $a$ et $b$ sont deux entiers naturels tels que $b\neq 0$, alors il existe deux entiers naturels $q$ et $r$ uniques, tels que $a=b.q+r$ et $r<b$. Les nombres $q$ et $r$ sont appelés respectivement le quotient et le reste de la division euclidienne de $a$ par $b$.
Démonstration
Nous démontrons d’abord l’existence de $q$ et de $r$. Soit $b\mathbb N$ l’ensemble des multiples de $b$, explicitement $b\mathbb N=\{b.d : d\in\mathbb N\}$, image de l’application $M_b:\mathbb N\to \mathbb N$, $d\mapsto b.d$ de « multiplication par $b$ ». L’ensemble $[[0,a]]=\{n\in\mathbb N : n\leq a\}$ est fini (voir le cours \no 3, chapitre 2), donc le sous-ensemble $b\mathbb N\cap [[0,a]]$ est fini également (idem); n’étant pas vide puisqu’il contient $0=b.0$, il possède alors un plus grand élément $k$ par le lemme 4.1 qui est de la forme $b.q$.
Par définition de $k$, on a $b.q\leq a$, donc par définition de $\leq$ il existe un entier naturel $r$ tel que $a=b.q+r$. Supposons par l’absurde que l’on a $r\geq b$ : par les propriétés de $\leq$ (proposition 3.5(iv)), on obtient $a=b.q+r\geq b.q+b=b.(q+1)$, ce qui entraîne que $b.(q+1)\in b\mathbb N\cap [[0,a]]$; comme $k=bq<b(q+1)=bq+b$, ceci contredit la définition de $k$, donc par reductio ad absurdum, on a $r<b$ et l’existence de $q$ et de $r$ est démontrée.
En ce qui concerne leur unicité, supposons que $q’,r’\in\mathbb N$ sont tels que $a=b.q’+r’$ avec $r'<b$; on obtient $b.q’\leq a <b.q’+b=b.(q’+1)$, donc $q’$ est le plus grand élément de $b\mathbb N\cap [[0,a]]$, soit $q=q’$, et $b.q+r=b.q+r’$; par le lemme 3.1(i), on obtient $r=r’$, et le théorème est démontré. $\square$
Remarque 4.6
Dans la démonstration de cet énoncé dans le cours \no 1, nous avons utilisé les propriétés intuitives de la soustraction dans l’ensemble $\mathbb Z$ et de la valeur absolue dans l’ensemble $\mathbb R$. Ici la propriété de simplifiabilité de l’addition dans $\mathbb N$ permet de se passer de la soustraction, tandis que l’usage du plus grand élément d’un ensemble fini permet de se passer de la valeur absolue.
La figure suivante représente représente une division euclidienne par « paquets ».
Définition 4.7
Si $a$ et $b$ sont deux entiers naturels avec $b>0$, on dit que $a$ est le dividende et $b$ le diviseur de la division euclidienne $a=b.q+r$.
Exemple 4.8
On a $527=48\times 10+47$; comme $47<48$, $10$ est le quotient et $47$ est le reste, de la division euclidienne de $527$ (dividende) par $48$ (diviseur).
Corollaire 4.9
Si $a$ et $b$ sont deux entiers naturels, avec $b\neq 0$, alors $b$ divise $a$ si et seulement si le reste de la division euclidienne de $a$ par $b$ est $0$.
Démonstration
Si $b|a$, alors il existe par définition $d\in\mathbb N$ tel que $a=b.d=b.d+0$, donc par unicité du quotient et du reste dans la division euclidienne de $a$ par $b$, $d$ est le quotient, et $0$ est le reste, de cette division. Inversement, écrivons la division euclidienne de $a$ par $b$ sous la forme $a=b.q+r$, avec $r<b$ : si $r=0$, on a $a=b.q$, donc $b|a$. $\square$
Remarque 4.10
Ce corollaire peut paraître évident, à cause de l’intuition de ce que signifie la division euclidienne, mais il est nécessaire de le démontrer.
Un entier naturel $d$ tel que $d$ divise $n$ est appelé un diviseur de $n$, et $n$ est alors appelé un multiple de $d$.
8.1 Exercices
Exercice 4.11
i) Démontrer par l’absurde le principe de récurrence à partir des deux premiers axiomes de Peano et de la proposition 4.3. Indication : si $S\subseteq \mathbb N$ est un sous-ensemble tel que $0\in S$ et $s(n)\in S$ dès que $n\in S$, supposer que $S\neq \mathbb N$, et considérer le plus petit élément du sous-ensemble non vide $\mathbb N-S$ de $\mathbb N$.
ii) Effectuer la division euclidienne de $247$ par $53$.
iii) Quel est le reste dans la division euclidienne de $114$ par $3$ ?
iv) Soient $a,b\in\mathbb N$, avec $b>0$. Supposons que $a<b$; quels sont le quotient et le reste de la division euclidienne de $a$ par $b$ ?
v) Soient $a,b\in\mathbb N$, avec $a>0$ et $b>1$. Montrer qu’il existe un unique entier naturel $n$ tel que $b^n\leq a<b^{n+1}$.
5. Les nombres premiers
Désolé, vous n'avez pas accès à tout MATHESIS::Essentiel sans abonnement. Pour vous abonner, rendez-vous sur MATHESIS - Adhésion
