Théorie élémentaire des ensembles [C1.I.4]
Après avoir introduit les notions de base de la théorie des ensembles (éléments et appartenance, sous-ensembles et inclusion) et les ensembles mathématiques naturels, notamment $\mathbb N$, $\mathbb Z$, $\mathbb Q$ et $\mathbb R$, ainsi que leurs propriétés dans le chapitre précédent, nous allons approfondir les bases de la théorie naïve des ensembles, évoquée dans la première section comme langage conceptuel de la mathématique moderne.
La fécondité de la méthode mathématique repose sur la clarification apportée par cette théorie, conjointement à l’élucidation de la logique mathématique qui lui correspond et que nous avons abordée dans le deuxième chaputre à propos de l’expression mathématique. Il y a ainsi une articulation naturelle et fondamentale entre la théorie naïve des ensembles et la logique mathématique naturelle, qui apparaîtra notamment dans les définitions ensemblistes.
Rappelons que la théorie naïve des ensembles repose sur l’intuition primitive des objets, des ensembles et des entiers naturels, ce qui signifie que nous ne définirons pas ces notions, mais que nous nous appuierons sur l’intuition que nous en avons.
1. Définitions et extensionnalité
1.1. Définitions par extension et par intension
Si la théorie naïve des ensembles et la logique mathématique naturelle forment l’armature conceptuelle de la théorie mathématique moderne, le point d’articulation fondamental entre les ensembles et le discours mathématique se situe au niveau des définitions des ensembles mathématiques.
En effet, il n’est possible de déployer un discours scientifique qu’à propos de ce dont on sait de quoi on parle… Le philosophe Ludwig Wittgenstein, dans un autre contexte, disait la chose suivante : « Ce qui peut être dit, peut être dit clairement; et ce dont on ne peut parler, il faut le passer sous silence ».
Nous avons vu qu’il était possible de se donner des ensembles « naturels », à partir de l’intuition de leurs éléments : nombres entiers, nombres rationnels, nombres réels… et de leurs propriétés, lesquelles sont elles-mêmes exprimées dans un langage qui reflète la théorie des ensembles.
A partir des ensembles définis par des notions primitives ou intuitives, il est alors nécessaire et possible d’en définir d’autres, grâce aux méthodes d’expression mathématique étudiées dans la deuxième section.
Il existe deux manières de définir un ensemble – mathématique ou non : la définition par extension et la définition par intension. Quelle que soit l’approche adoptée, la définition d’un ensemble se fait en utilisant la notation des crochets $\{$ et $\}$.
Un ensemble est défini \textbf{par extension} lorsqu’on se donne une liste (exhaustive) de ses éléments; par exemple, l’ensemble $\{0,3,5,6,8,15\}$ est défini par extension.
Dans cette situation, on écrit simplement dans la description tous les (noms des) éléments de l’ensemble entre crochets : si $a,b,c,\ldots$ sont les éléments de l’ensemble qu’on cherche à décrire, on écrit $\{a,b,c,\ldots\}$ (ici les points de suspension servent de notation générique, mais la description doit être explicite et finie).
Il peut être utile de répéter le nom d’un objet dans une définition par extension : on décrit cependant le même ensemble. Par exemple, les ensembles $\{1,8,2\}$ et $\{1,8,2,8\}$ sont identiques. L’ordre dans lequel on liste les éléments n’a pas non plus d’importance.
Un ensemble est défini par intension lorsqu’on se donne une propriété qui détermine cet ensemble. C’est à ce niveau que l’expression mathématique spécifique s’articule à la théorie naïve des ensembles.
Par exemple, l’ensemble des entiers naturels pairs, déjà évoqué, est l’ensemble noté $\{n\in\mathbb N : \exists d\in\mathbb N,\ n=2.d\}$ et est défini par intension comme sous-ensemble de l’ensemble $\mathbb N$ des entiers naturels, par la clause « $\exists d\in\mathbb N,\ n=2.d$ ».
En général, un ensemble est défini par intension lorsqu’il s’agit d’un sous-ensemble d’un ensemble déjà introduit ou défini, constitué des éléments ayant une certaine propriété.
On utilise en mathématique les deux types de définitions. Cependant, la définition par extension ne permet par sa nature que de définir des ensembles « finis » (notion que nous définirons proprement dans le Chapitre 2). Pour définir des ensembles « infinis », il est donc naturel de recourir à la définition par intension, qui est donc la définition mathématique par excellence.

1.2. Définitions et clauses
La logique du langage mathématique est étroitement corrélée à l’objet de la science mathématique; ceci apparaîtra lorsque nous décrirons les relations entre certaines « opérations » fondamentales sur les ensembles et les opérations logiques des propriétés qui les définissent.
Lorsque l’on définit un sous-ensemble par intension, c’est-à-dire à partir d’une propriété, on « choisit » à l’aide de cette propriété certains éléments d’un ensemble donné. Pour cela, on utilise une expression mathématique, sous forme symbolique ou non, qui ne contient donc – pour l’instant – qu’une seule variable libre pour les éléments de l’ensemble en question (nous nuancerons lors du deuxième chapitre).
Plus précisément, si $E$ est un ensemble et qu’on veuille définir un sous-ensemble $S$ par une propriété $P$, alors $P$ ne peut contenir qu’une seule variable libre $x$ pour les éléments de $E$, si bien qu’on peut écrire ceci formellement : $S=\{x\in E : P(x)\}$, lire « $S$ est l’ensemble des éléments $x$ de $E$ qui ont la propriété $P$ », plus sommairement « l’ensemble des $x\in X$ tels que $P$ ».
Dans la deuxième section (REF), nous avons évoqué la notion de clauses logiquement équivalentes : par définition même de cette notion, il faut noter ici que si $P(x)$ et $Q(x)$ sont deux clauses équivalentes avec une variable libre $x$ pour les éléments d’un ensemble $E$, alors $P$ et $Q$ définissent le même sous-ensemble de $E$, autrement dit les ensembles $\{x\in E : P(x)\}$ et $\{x\in E : Q(x)\}$ sont égaux.
Notons enfin qu’il ne faut pas confondre les définitions de notions mathématiques au sens de la deuxième section, et les définitions de sous-ensembles par des propriétés.
Exemple 1.1
i) Les sous-ensembles $S=\{x\in \mathbb R : |x|=x\}$ et $\mathbb R_+=\{x\in \mathbb R : x\geq 0\}$ de $\mathbb R$ sont égaux.
ii) Si $n\in\mathbb Z$, en général le nombre rationnel $n/2$ n’est pas dans $\mathbb Z$ : c’est le cas si et seulement si $n$ est pair. Ainsi, les sous-ensembles $X=\{n\in \mathbb Z : \exists d\in\mathbb Z,\ 2.d=n\}$ et $Y=\{n\in\mathbb Z : n/2\in \mathbb Z\}$ de $\mathbb Z$ sont égaux : il s’agit de l’ensemble des entiers relatifs pairs.
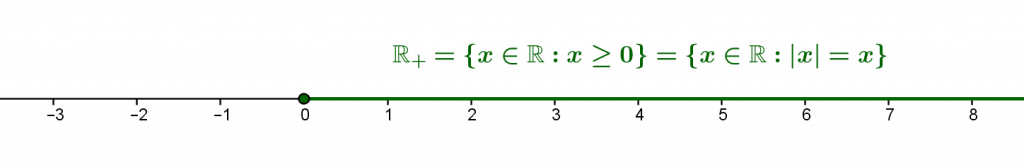
1.3. Extensionnalité et inclusion
L’intuition des notions d’ensemble et d’appartenance entraîne que si l’on se donne « deux » ensembles $E$ et $F$, c’est-à-dire deux descriptions d’ensembles, on a décrit le même ensemble, c’est-à-dire que $E=F$, lorsque $E$ et $F$ ont les mêmes éléments.
On appelle ce principe le principe d’extensionnalité, qui au niveau de la théorie naïve des ensembles, est purement « analytique », ce qui signifie qu’il est présent implicitement dans la notion elle-même.
Lorsque nous avons abordé la notion de sous-ensemble, nous avons défini la relation d’inclusion $E\subseteq F$ par : tout élément de $E$ est élément de $F$, symboliquement : $\forall x\in E,\ x\in F$. Il s’ensuit que deux ensembles $E$ et $F$ sont égaux exactement lorsque $E\subseteq F$ et $F\subseteq E$.
Pour démontrer l’égalité de deux ensembles $E$ et $F$ donnés formellement, on procède ainsi souvent qu’on démontre que $E\subseteq F$, et que $F\subseteq E$ : on dit qu’on procède par double inclusion.
Lorsqu’on se donne deux sous-ensembles $S$ et $T$ d’un même ensemble $E$, définis respectivement par deux propriétés $P$ et $Q$, $S$ et $T$ sont donc égaux exactement lorsque $P$ et $Q$ définissent le même sous-ensemble, c’est-à-dire lorsque $P(x)$ et $Q(x)$ (où $x$ est une variable pour les éléments de $E$) sont logiquement équivalentes, par le paragraphe précédent.
Dans cette situation, démontrer la validité universelle de l’implication $P\Rightarrow Q$ (c’est-à-dire la « moitié » de l’équivalence $P\Leftrightarrow Q$) revient alors à démontrer que pour tout élément $x$ de $E$ tel que $P(x)$ est vraie, alors $Q(x)$ est vraie, c’est-à-dire que si $x\in S$, alors $x\in T$, soit encore que $S\subseteq T$.

1.4. Exercices
Exercice 1.2
i) Donner une description par extension de l’ensemble des entiers relatifs impairs dont la valeur absolue est inférieure à $10$. Les représenter sur un dessin.
ii) Donner une définition par intension, en utilisant une clause symbolique, de l’ensemble des entiers naturels multiples de $3$.
iii) Donner une autre définition par intension de l’ensemble $[-1,1]=\{x\in \mathbb R : -1\leq x\leq 1\}$ des nombres réels compris entre $-1$ et $1$, en utilisant la valeur absolue.
iv) Donner deux définitions différentes de l’ensemble des entiers naturels impairs.
2. Opérations élémentaires sur les ensembles
Désolé, vous n'avez pas accès à tout MATHESIS::Essentiel sans abonnement. Pour vous abonner, rendez-vous sur MATHESIS - Adhésion
