Utilisation de ME

Quelques précisions sur l’interface de MATHESIS :: Essentiel (ME).

1.Moteur de recherche interne dans ME

L’utilisation de ME est intuitive et directe. Le moteur de recherche apparaissant sur la page principale et en haut de chaque page peut être utilisé pour trouver un terme, une expression, un sujet… Par exemple, pour trouver des références sur les entiers naturels, nous écrivons l’expression « entier naturel » dans la barre de recherche :

En cliquant sur « Rechercher », ME vous propose une liste d’articles dans lesquels vous pouvez trouver des précisions sur les entiers naturels, et vous pouvez choisir quelle entrée répondra à vos questions en cliquant sur le titre de la référence correspondante :

Par exemple, si vous cherchez des précisions ou des compléments sur l’arithmétique des entiers naturels, en choisissant l’entrée « Arithmétique naturelle » (n°4 dans la liste des résultats), vous accédez directement à la leçon/l’article sur le sujet (dont nous détaillons la structure générale dans la suite de l’article) :

2.Interface des cours/chapitres

Chaque cycle est identifié sur la page d’accueil par un bloc de cours (5 ou 6), identifié à l’année et au semestre correspondants. Par exemple, le Cycle 2 correspond au deuxième semestre de la première année, et le cours/chapitre n°3 de ce cycle est « Arithmétique des Nombres et des Fonctions » :

Pour accéder à un cours/chapitre en particulier, il suffit de cliquer sur l’icône à gauche de la section désirée, qui fera apparaître la structure du cours en différentes parties (ici le cours/chapitre n°2 du Cycle 1, « Du Fini à l’Infini Mathématique ») :

En développant de la même manière chaque section du cours/chapitre choisi en cliquant sur l’icône correspondant, on fait apparaître les leçon(s)/articles qu’elle contient. Par exemple, ici la 5ème leçon du cours/chapitre n°2 du Cycle 1 (numérotée [C1.II.5]), intitulée « L’Infini Mathématique », est l’unique article de la section éponyme « L’infini mathématique ». Il suffit alors de cliquer sur la leçon affichée avec l’icône de texte pour accéder à l’article désiré par la page d’accueil.

3.Structure des leçons/articles

Chaque leçon/article se présente comme suit, de la même manière que sur la page présente :

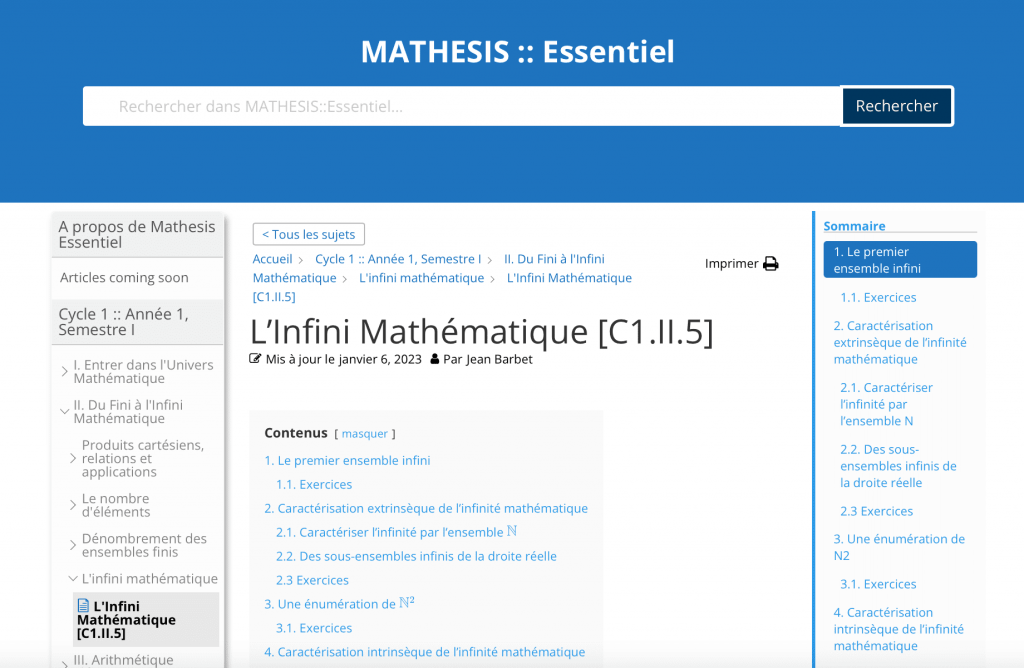
En particulier, vous avez toujours accès en haut de la page au moteur de recherche interne de MATHESIS :: Essentiel.

3.1.Référence de la leçon/l’article

Le titre de chaque article précise sa place dans le corpus par un code, ici [C1.II.5], soit la leçon n°5 du Chapitre II du Cycle 1.

Au-dessus du titre de l’article apparaît l’arborescence complète où il se situe dans le corpus. En cliquant sur n’importe quel niveau, vous accédez aux archives de la catégorie correspondante, qui recense les leçons/articles auxquelles vous pouvez accéder directement, ici l’ensemble des leçons/articles du chapitre III du Cycle 1 :

L’arborescence est aussi reproduite en détail sur la colonne de gauche, où vous retrouvez en gras la leçon/article en cours, et où pouvez à tout moment accéder à n’importe quel article comme sur la page d’accueil :

3.2.Sommaire de la leçon/l’article

L’en-tête de l’article, après le titre, contient une table des matières interactive qui vous permet d’accéder directement aux sections de la leçon qui vous intéressent. Ce sommaire est aussi affiché en détail dans la colonne de droite, qui reste accessible pendant toute la lecture de l’article, notamment pour les renvois internes; ici, la table des matières et le sommaire interactifs de la leçon n°1 du cours/chapitre II du Cycle 1, « Produits, relations et applications » :

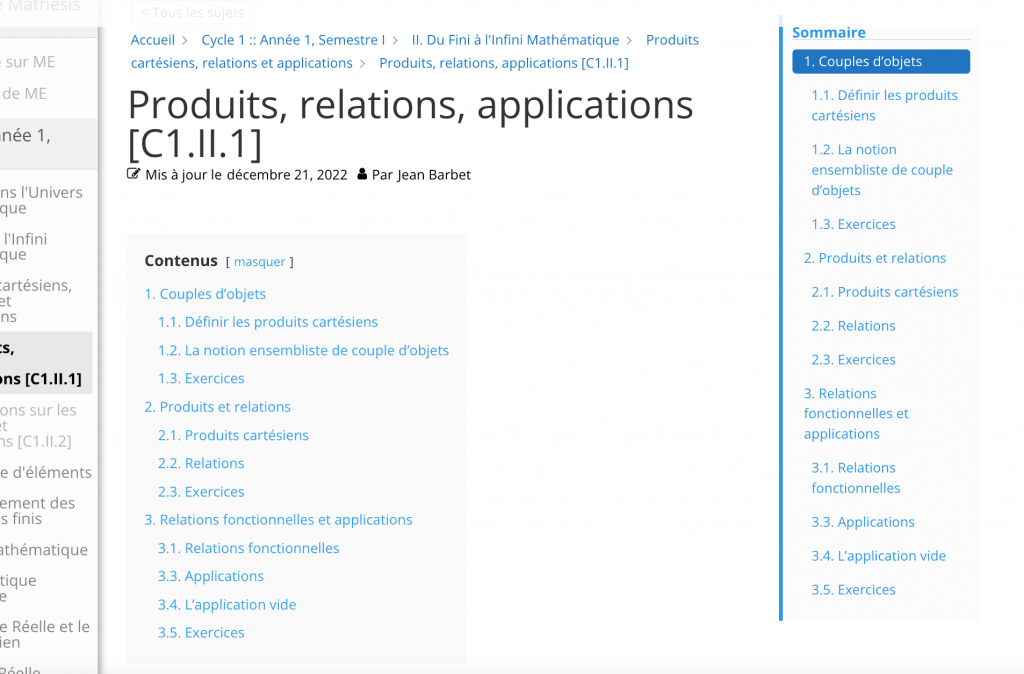
ATTENTION : Le sommaire de la leçon/l’article n’apparaît en entier que pour les utilisateurs abonnés et connectés. En mode découverte ou déconnecté, seul le sommaire de la première section, accessible librement, est développé.

3.3.Organisation des leçons/articles

Le corps des leçons/articles est organisé comme un article électronique standard : avec des sections, sous-sections et paragraphes, des illustrations… Voici un aperçu de la sous-section 1.1 de la leçon/article [C1.II.1] intitulée « Produits, relations et applications », que vous pouvez retrouver (en accès libre comme la première section de chaque article) ici :

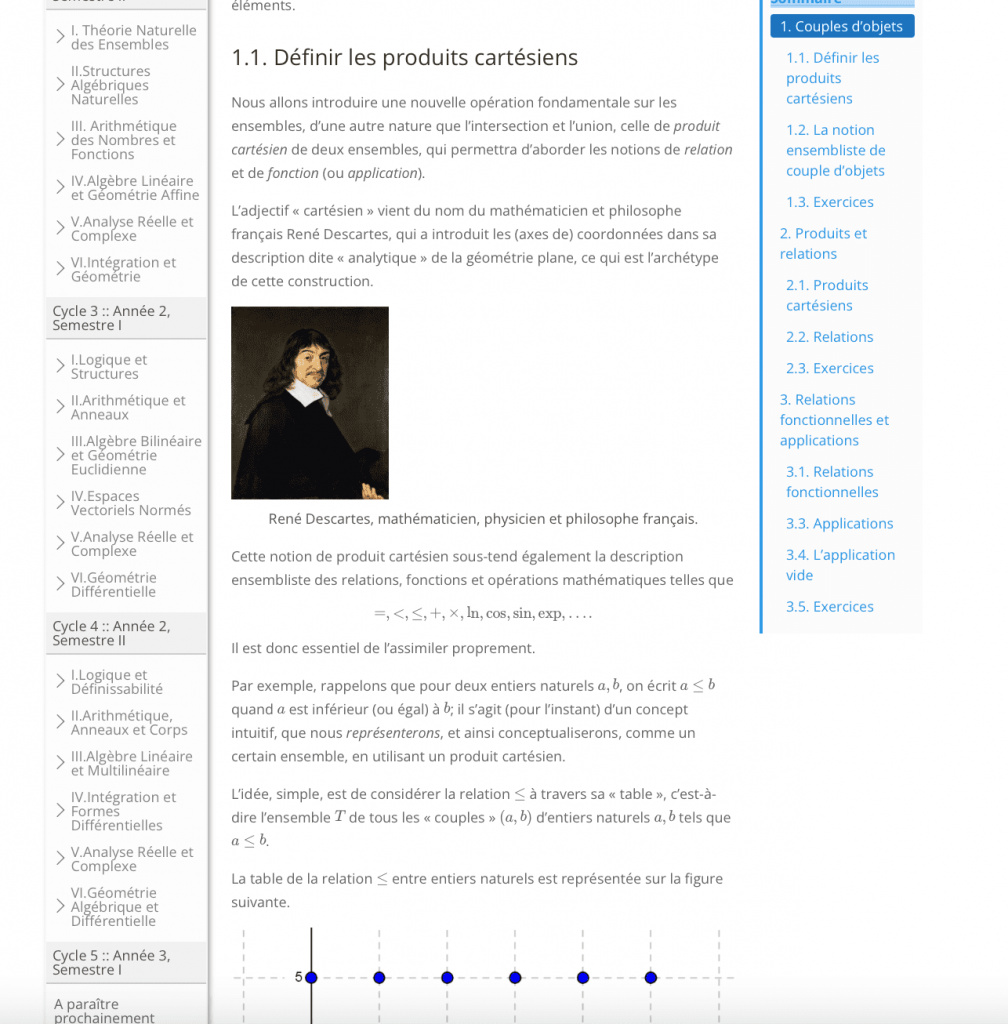
Les leçons/articles sont aussi organisés comme une section d’un manuel de mathématiques supérieures : avec des définitions, des notations, des exemples, des théorèmes (différenciés en propositions, lemmes, théorèmes, corollaires), des démonstrations, des exercices, des problèmes… mis en évidence dans le texte et numérotés pour faciliter l’accès aux références internes et externes. Voici un aperçu d’un lemme (résultat préparatoire) et d’une proposition (avec une partie de sa démonstration) se trouvant dans la leçon/l’article [C1.II.5] « L’infini mathématique » (à propos de l’existence d’une infinité de nombres rationnels et irrationnels dans les intervalles réels) :

4.Lecture/étude dynamique des leçons/articles

Le contenu des leçons/articles est dynamique. Cela signifie que les références nécessaires à la compréhension du texte sont accessibles directement depuis la section en cours de lecture, par des liens hypertextes – signifiés de manière standard, en bleu et soulignés – à l’intérieur même de MATHESIS :: Essentiel. Ainsi, le corpus est « auto-contenu » et vous n’avez pas besoin de faire des recherches longues et fastidieuses pour compléter les pré-requis de votre lecture/étude, ou relire/retrouver certains éléments. Vous trouverez essentiellement deux types de références dynamiques, des références internes (à l’intérieur de l’article) et des références externes (dans une autre section ou un autre article).

4.1.Utilisation des références internes

Les références internes renvoient à un élément de la leçon/l’article elle-même : une définition, une proposition, une section… En cliquant sur une référence interne, vous êtes renvoyé à la destination à l’intérieur du même onglet. Par exemple, dans la section 2.1 de la leçon/l’article [C1.III.3] (3ème leçon du cours 3 du cycle 1…) intitulée « Axiomes et structure de l’ensemble $\mathbb Z$ des entiers relatifs », nous avons besoin de faire référence à une section précédente (1.1, lien en bleu) :

En cliquant sur le lien, on est redirigé à la section en question à l’intérieur du même onglet :

Pour prendre un autre exemple dans la même leçon, afin de démontrer les propriétés de l’ordre relativement à l’addition des nombres entiers relatifs (Proposition n°3), nous avons besoin d’utiliser un résultat démontré auparavant (Proposition n°2). Dans ce cas, le lien à cet élément est signifié dans le texte de la démonstration :

En cliquant sur le lien, vous accédez directement à l’énoncé de la proposition n°2, afin de pouvoir le relire pour suivre l’argumentation de la démonstration de la proposition n°3 :

Notez qu’à l’intérieur d’une même sous-section, une référence dynamique n’apparaît qu’une fois : vous pourriez donc avoir à rechercher le lien dynamique de la référence le plus proche pour accéder à son contenu. Alternativement, vous pouvez aussi faire sans peine une recherche manuelle, grâce à la numérotation des éléments ou au sommaire qui se trouve à droite.

4.2.Utilisation des références externes

Les références externes fonctionnent sur le même principe que les références internes : elles renvoient aux mêmes types d’éléments, mais dans d’autres leçons/articles. Elles sont signifiées également par un lien hypertexte, complété en général par le titre de la section ou de l’article dans laquelle se trouve la référence, l’ensemble étant présenté entre crochets (c’est-à-dire [ et ]). En cliquant sur le lien, vous êtes renvoyés automatiquement à la destination dans un autre onglet, afin de ne pas quitter la lecture de la leçon en cours. Par exemple, dans le même article, nous avons besoin de faire référence à deux autres sections, l’une dans le même cours/chapitre, l’autre dans un autre chapitre :

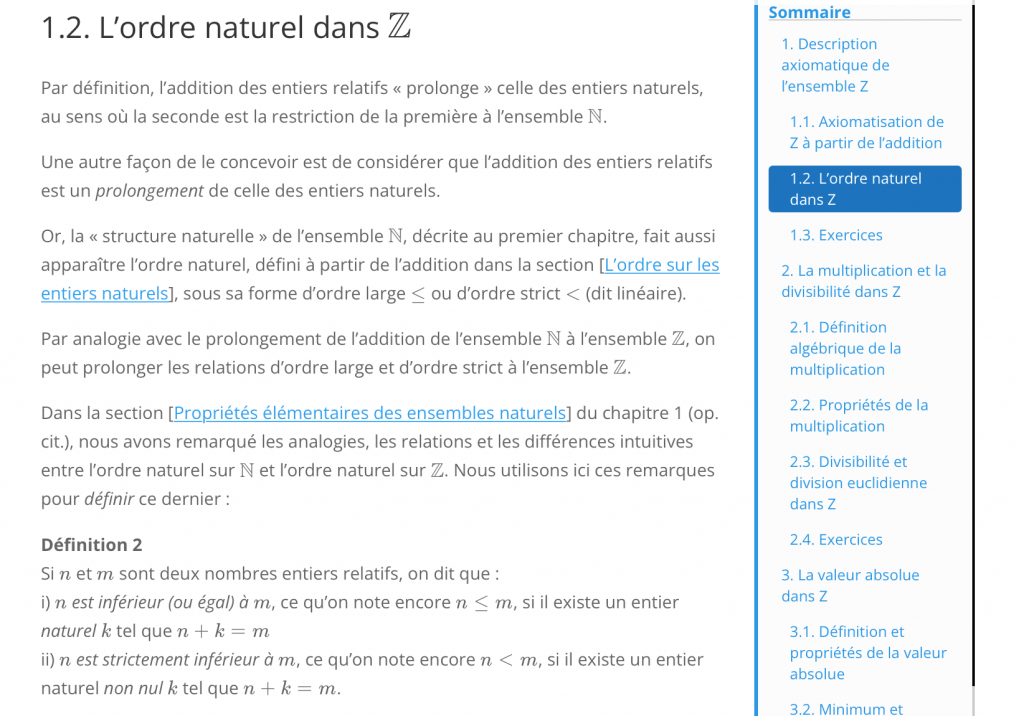
La première, identifiée comme [L’ordre sur les entiers naturels], renvoie au même cours/chapitre, donc seul le titre de la section est indiqué dans le contexte. La seconde, [Propriétés élémentaires des ensembles naturels], renvoie à une section d’un autre chapitre, indiqué ici dans le contexte. En cliquant par exemple sur cette seconde référence, un autre onglet s’ouvre directement à la page de destination, ici un article :

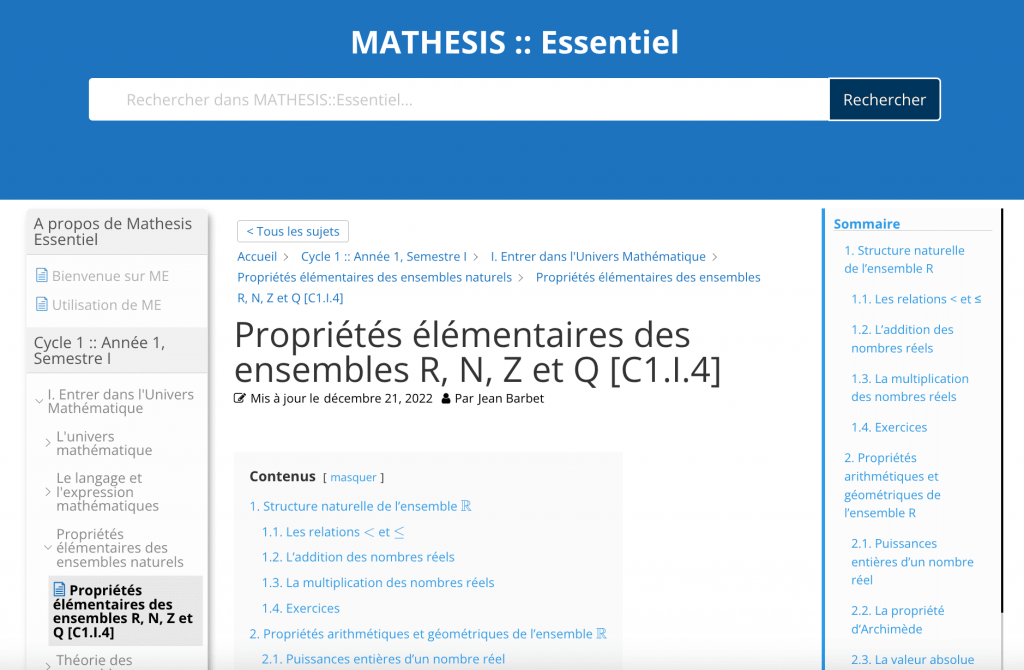
Lorsque la référence externe est plus précise, c’est-à-dire lorsqu’elle concerne un élément spécifique d’une autre leçon (une définition, une proposition, un exercice, une section…), l’élément est donné en référence avec l’article entre crochets, et c’est sur l’élément qu’il faut cliquer pour accéder à la destination, toujours dans un nouvel onglet. Par exemple, dans la même leçon, pour démontrer la proposition n°2, nous avons besoin d’utiliser le lemme 1 d’un article précédent, identifié dans la preuve par « [Axiomes et structure de l’ensemble $\mathbb N$, lemme 1(ii)] » :

En cliquant sur le lien, vous êtes renvoyés directement à l’énoncé du lemme 1 de la leçon/l’article « Axiomes et structure de l’ensemble $\mathbb N$ », dans un nouvel onglet, où vous pouvez consulter comme une annexe la référence dont vous avez besoin :

Certaines références externes sont répétées dans la même leçon/article, jamais à l’intérieur d’une sous-section (comme pour les références internes). Certaines références externes pointent également vers d’autres éléments d’une même leçon déjà invoquée en référence. Vous avez le choix dans ce cas entre accéder directement à la référence en ouvrant un nouvel onglet, et utiliser directement l’onglet déjà ouvert pour faire cette fois-ci une recherche interne. Par exemple, toujours dans la même leçon, pour démontrer la proposition n°5 sur les propriétés élémentaires de la multiplication, vous avez besoin de la proposition n°4 du même article déjà appelé :

Si vous cliquez sur le lien, vous êtes renvoyé, dans un nouvel onglet, directement à cette proposition. Mais si vous avez conservé l’article ouvert, consulté à la référence précédente, vous pouvez directement y chercher la proposition n°4. Tout ceci est très intuitif et vous développerez vos propres préférences avec la pratique et en fonction de votre support.

5.Questions et commentaires

Vous pouvez commenter les leçons/articles en tant qu’utilisateur inscrit, dans la section Commentaires en bas de page. Ces commentaires peuvent être édités, et vous pouvez notamment y poser vos questions sur le cours, afin d’obtenir des précisions ou des éclaircissements, de ma part ou de la part d’autres participants. Nous pourrons ainsi compléter la leçon/l’article par une discussion interactive comme sur un forum. Voici un exemple de la section commentaires sur le même article :

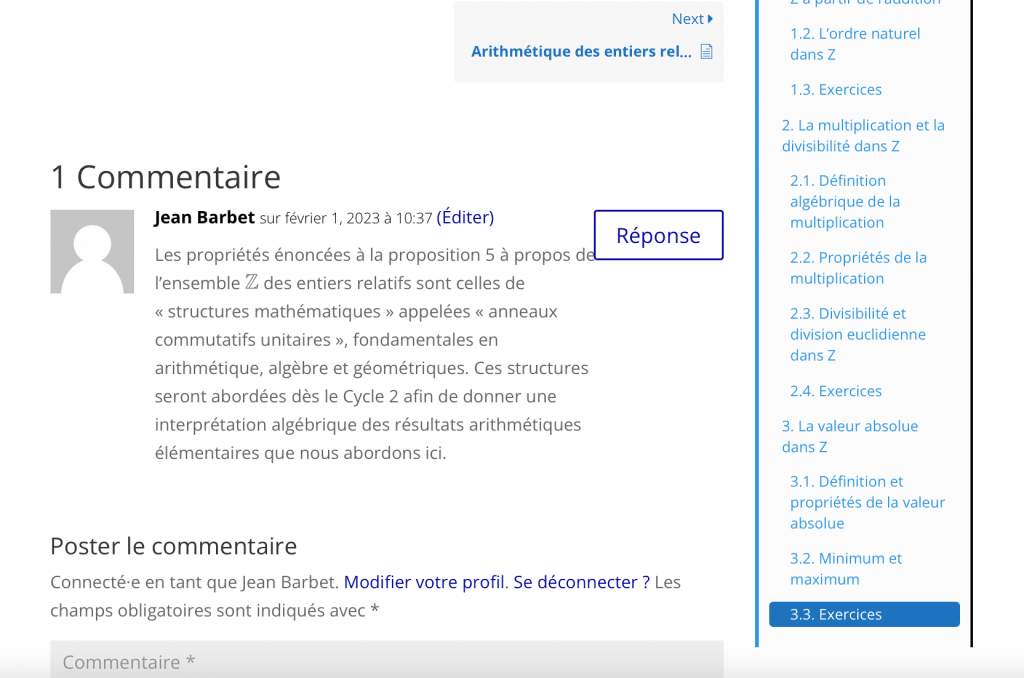
Vous pouvez constater qu’il est possible d’utiliser, pour ceux qui le connaissent, le langage d’écriture mathématique LaTeX dans la section Commentaires (ici employé pour écrire le symbole $\mathbb Z$ de l’ensemble des entiers relatifs) , ce qui permet d’ajouter des formules, des équations, etc…

Nous vous demanderons de veiller à n’écrire des commentaires qu’en relation avec l’article/la leçon en cours, et de respecter les règles élémentaires de courtoisie en vigueur dans tout espace de discussion, virtuel ou non.