L’ensemble $\mathbb Q$ des nombres rationnels [C1.III.3]

Dans le chapitre [L’ensemble $\mathbb Z$ des nombres entiers relatifs], nous avons abordé l’axiomatisation de l’ensemble $\mathbb Z$ des nombres entiers relatifs, comme « extension » de l’ensemble $\mathbb N$ des nombres entiers naturels, à partir d’une description de l’addition dans $\mathbb Z$.

Les propriétés de l’addition, de la multiplication, de l’ordre naturel et de la divisibilité dans $\mathbb Z$ ont alors été établies à partir des propriétés de leurs contreparties dans $\mathbb N$ (dérivant elles-mêmes des axiomes de Peano), et des deux axiomes de l’addition dans $\mathbb Z$.

Ainsi, nous avons pu approfondir de manière substantielle l’arithmétique élémentaire grâce à l’opération de soustraction, et fonder par là ce premier étage de la théorie des nombres sur quelques cinq axiomes assez simples.

Dans cette section, nous poursuivons notre approche scientifique de la théorie des ensembles naturels de nombres par la description, à nouveau axiomatique, de l’ensemble $\mathbb Q$ des nombres rationnels, et par l’extension de concepts et propriétés arithmétiques déjà évoqués pour les ensembles $\mathbb N$ et $\mathbb Z$.

Nous prolongerons également la « structure naturelle » (addition, multiplication et ordre), de $\mathbb Z$ à $\mathbb Q$, avec une exception notable, celle de la divisibilité : par définition, cette relation ne présente plus aucun intérêt dans $\mathbb Q$, si bien qu’il nous faut considérer d’autres manière d’aborder l’arithmétique des nombres rationnels, notamment à travers les « valuations », généralisations des exposants des nombres premiers.

Dans l’ensemble $\mathbb Q$ apparaissent également, par « densité » de l’ordre, les premières notions et propriétés géométriques, qui sont ici essentiellement associées aux notions et propriétés arithmétiques, ce qui nous permettra d’entrer de plain pied dans la géométrie au cours suivant. C’est notamment l’occasion de parler de commensurabilité, l’analogue rationnel de la recherche du plus grand diviseur commun, qui illustre une forme de « passage » de l’arithmétique à la géométrie.

1.Description axiomatique de l’ensemble $\mathbb Q$

Comme nous l’avons fait pour l’ensemble $\mathbb N$ et pour l’ensemble $\mathbb Z$, nous admettons ici l’existence d’un ensemble $\mathbb Q$ des nombres rationnels, que nous concevons encore de manière intuitive comme dans le chapitre 1, et qui contient l’ensemble $\mathbb Z$ comme sous-ensemble.

Comme pour l’ensemble $\mathbb Z$ (Chapitre 2), nous ne démontrons pas « l’existence » de cet ensemble, que nous construirons au semestre II, mais nous en donnons une description par des axiomes.

1.1.Axiomatisation de $\mathbb Q$ à partir de la multiplication

Dans le chapitre [L’ensemble $\mathbb N$ des nombres entiers naturels], l’axiomatique de Peano a permis de reconstituer toute la « structure naturelle » de l’ensemble $\mathbb N$, essentiellement l’addition puis la multiplication, à partir de la fonction successeur (les relations d’ordre et de divisibilité étant définies à partir des opérations $+$ et $\times$).

Dans le chapitre C1.III.2, c’est à partir de l’addition que nous avons axiomatisé l’ensemble $\mathbb Z$, pour définir ensuite la multiplication des entiers relatifs à partir de leur addition et de la multiplication des entiers naturels. En effet, la différence essentielle entre les ensembles $\mathbb N$ et $\mathbb Z$, c’est que dans $\mathbb Z$ on peut opposer tout élément, autrement dit soustraire les nombres.

Dans cette avant-dernière section du chapitre, c’est à partir de la multiplication que nous axiomatisons l’ensemble $\mathbb Q$, pour définir ensuite l’addition, à partir de l’addition des entiers relatifs et de la division. La différence essentielle entre les ensemble $\mathbb Z$ et $\mathbb Q$ réside en effet dans la possibilité d’inverser tout nombre non nul, et donc de diviser par un tel nombre.

Nous admettons donc l’existence d’une application de multiplication $\times:\mathbb Q\times\mathbb Q\to \mathbb Q$, prolongeant la multiplication des entiers relatifs, et possédant les propriétés axiomatiques suivantes (à comparer avec [Axiomes et structure de l’ensemble $\mathbb Z$, axiome 4] :

Axiome 6
i) Pour tout $r\in\mathbb Q$, on a $1.r=r$
ii) Pour tous $q,r\in\mathbb Q$, on a $q.r=r.q$ (la multiplication est commutative)
iii) Pour tous $q,r,s\in\mathbb Q$, on a $(q.r).s=q.(r.s)$ (la multiplication est associative)
iv) Pour tout $r\in\mathbb Q$, non nul, il existe $q\in \mathbb Q$ tel que $r.q=1$ (tout élément non nul possède un inverse pour la multiplication).

Remarque 1.1
Dire que la multiplication des nombres rationnels prolonge celle des entiers relatifs, cela signifie que pour $n,m\in\mathbb Z$, le résultat de l’opération $n.m$ dans $\mathbb Q$ (puisque $\mathbb Z\subseteq\mathbb Q$) est le produit $n.m$ tel qu’il a été défini à la section [C1.III.2, Multiplication des entiers relatifs], ou encore, que la multiplication $\times_\mathbb Z:\mathbb Z^2\to \mathbb Z$ des entiers relatifs est la restriction de $\times$ à $\mathbb Z$, soit $\times_\mathbb Z=\times|_{\mathbb Z}$.

Par la propriété (iv) de l’axiome 6, tout nombre rationnel non nul possède un inverse pour la multiplication : c’est la propriété fondamentale que ne possède pas l’ensemble $\mathbb Z$ et qui fait l’intérêt arithmétique et géométrique de l’ensemble $\mathbb Q$.

L’inverse (multiplicatif) $q$ d’un nombre rationnel $r$ est nécessairement unique : en effet, si $s\in\mathbb Q$ et $r.s=1$, alors on a $q=1.q$ (par (i)) $=q.1$ (par (ii)) $=q.(r.s)=(q.r).s$ (par (iii)) $=(r.q).s$ (par (ii)) $=1.s=s.1$ (par (ii)) $=s$ (par (i)). On note $1/r$ ou $\dfrac 1 r$ l’inverse de $r$, et on définit le quotient $r/s$ de deux nombres rationnels $r$ et $s$, avec $s\neq 0$, comme le nombre rationnel $r\times (1/s)$.

Définition 1.2
L’application $/:\mathbb Q\times\mathbb Q^*\to \mathbb Q$, qui associe à un couple de nombres rationnels $(r,s)$, avec $s$ non nul, le quotient $r/s=r.(1/s)$, est la division des nombres rationnels. On rappelle que $\mathbb Q^*$ est l’ensemble des nombres rationnels non nuls.

Les propriétés de l’axiome 6 ne suffisent pas à caractériser l’ensemble $\mathbb Q$, c’est-à-dire à le décrire de manière essentiellement unique. Pour compléter cette description axiomatique, il nous faut introduire un axiome fondamental, analogue à [Axiomes et structure de l’ensemble $\mathbb Z$, axiome 5], qui permet de situer les nombres rationnels par rapport aux entiers relatifs :

Axiome 7
Pour tout nombre rationnel $r$, il existe un entier naturel $d$ tel que $r.d$ est entier.

On peut alors démontrer que l’ensemble $\mathbb Q$ ainsi décrit est « essentiellement unique ».

L’axiome 7 est équivalent à la propriété suivante, qui permet de donner une représentation des nombres rationnels :

Proposition 1.3
Si $r$ est un nombre rationnel, alors il existe un entier relatif $a$ et un entier relatif $b$ non nul, tels que $r=a/b$, et on peut toujours supposer que $b$ est un entier naturel.

Démonstration
Par l’axiome 7, il existe un entier naturel $d$ tel que $r.d\in\mathbb Z$. Posons $a=r.d$ : on a $a/d=a.(1/d)=(r.d).(1/d)=r.(d.(1/d))=r.1$ (par définition de l’inverse) $=r$, si bien que $a=r.d$ et $b=d$ conviennent, puisque $d$ est un entier naturel. $\square$

La figure suivante propose une représentation géométrique des nombres rationnels comme droites vectorielles du plan passant par des points à coordonnées entières (voir le livre 4).

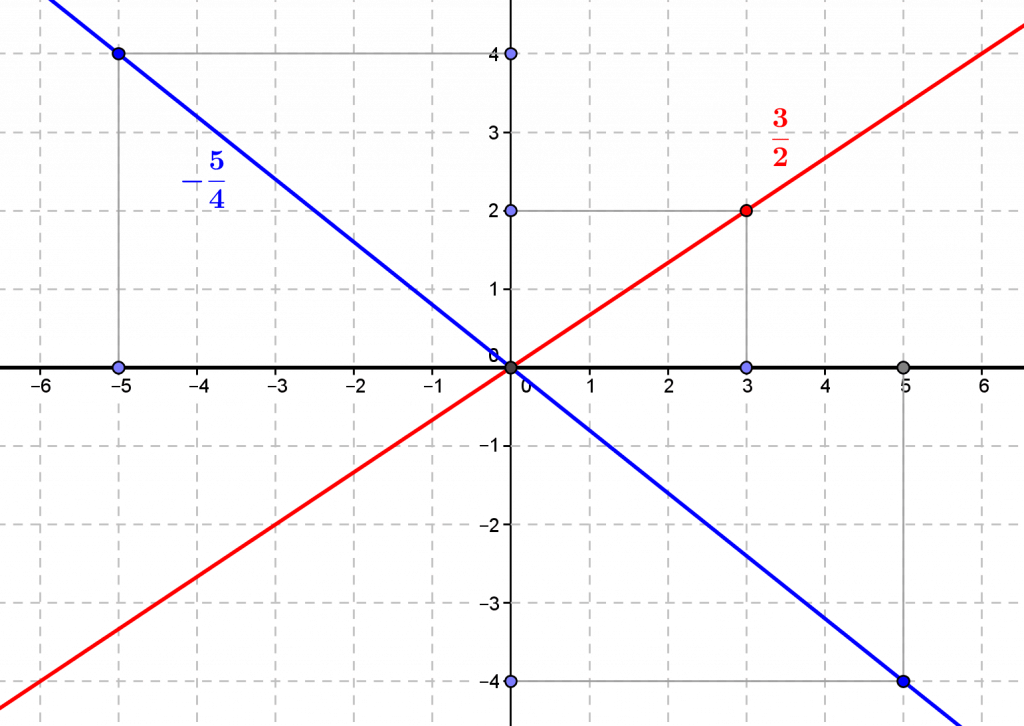
Le quotient $a/b$ d’un entier relatif par un entier relatif non nul est donc toujours défini comme nombre rationnel, et inversement un nombre rationnel peut donc toujours s’écrire sous la forme d’un quotient $a/b$, où $a\in\mathbb Z$ et $b\in\mathbb Z^*$ : les nombres rationnels sont donc toutes les « fractions » de la forme $a/b$, pour $a\in\mathbb Z$ et $b\in\mathbb Z^*$.

Cependant, une telle écriture d’un nombre rationnel n’est jamais unique : par exemple, le nombre rationnel $1/2$ s’écrit aussi sous la forme $(-7)/(-14)$ et en général sous la forme $n/2n$ pour tout entier relatif $n$ non nul. En fait, si $r$ est un nombre rationnel et $r=a/b$, pour tout nombre entier relatif $n$ non nul l’entier $n.b$ est non nul par [C1.III.2, théorème 2.6], si bien qu’on a $r=n.a/n.b$, comme l’indique, parmi d’autres propriétés, la proposition suivante :

Proposition 1.4
i) Si $a$ et $b$ sont deux entiers relatifs non nuls, on a $1/ab=(1/a).(1/b)$.
ii) Si $r=a/b$ est un nombre rationnel et $n$ est un entier relatif non nul, alors on a $a/b=na/nb$.
iii) Si $a,b,c,d$ sont des entiers relatifs et $b,d\neq 0$, on a $a/b=c/d$ si et seulement si $ad=cb$.

Démonstration
i) Par définition, $1/ab$ est l’unique nombre rationnel $r$ tel que $(ab).r=1$. Or, on a $(ab).((1/a).(1/b))=a.b.(1/b).(1/a)$ (par les propriétés de la multiplication) $=a.(1/a)$ (puisque $b.(1/b)=1$) $=1$, d’où $1/ab=(1/a).(1/b)$.
ii) On a $na/nb=(na).(1/nb)$ (par définition de la division) $=(na).((1/n).(1/b))$ (par (i)) $=a.n.(1/n).(1/b)=a.(1/b)=a/b$.
iii) Supposons que $a/b=c/d$ : on a $a.(1/b)=c.(1/d)$, et en multipliant chaque membre par $bd$, on obtient par les propriétés de la multiplication $a.d=a.(1/b).b.d=c.(1/d).b.d=c.(1/d).d.b=c.b$. Inversement, si $ad=cb$, comme $bd\neq 0$ par [C1.III.2, théorème 2.6] (op. cit.), on peut diviser les deux membres par $bd$ pour obtenir $a/b=ad/bd$ (par (ii)) $=ad.(1/bd)=ad.(1/b).(1/d)$ (par (i)) $=cb.(1/b).(1/d)=c.(1/d)=c/d$. $\square$

Exemple 1.5
Les nombres rationnels $207/(-92)$ et $(-72)/32$ sont égaux, puisque $207\times 32=6624=(-92).(-72)$.

La caractérisation de l’égalité des nombres rationnels à partir de leurs représentations donnée au (iii) de la proposition 1.4 est à la base de la construction que nous donnerons de l’ensemble $\mathbb Q$ au deuxième semestre.

1.2. Formes irréductibles d’un nombre rationnel

Si $r$ est un nombre rationnel et $r=a/b$, le couple $(a,b)$ sera appelé une représentation de $r$. Le nombre $a$ est appelé le numérateur\index{Numerateur@Numérateur} et $b$ le dénominateur\index{Denominateur@Dénominateur}, de la représentation.

Parmi ces représentations, qui rappelons-le sont en nombre infini (en bijection avec $\mathbb Z^*$ par la proposition 1.4), il en existe toutefois deux qui sont privilégiées, au sens où elles sont « les plus simples » : il s’agit des formes irréductibles du nombre $r$.

En effet, écrivons $r=a/b$ pour $a\in\mathbb Z$ et $b\in\mathbb Z^*$. Soit $d$ le p.g.c.d de $a$ et $b$ (section [C1.III.2, Nombres premiers entre eux]), de sorte qu’on peut écrire $a=\alpha.d$ et $b=\beta.d$, avec $(\alpha,\beta)\in\mathbb Z\times \mathbb Z^*$ : on a alors $a.\beta.d=ab=ba=b.\alpha.d$, et comme $d\neq 0$, par intégrité de la multiplication dans $\mathbb Z$ ([Axiomes et structure de l’ensemble $\mathbb Z$, théorème 1], op. cit.), on en déduit que $a.\beta=b.\alpha$, autrement dit que $r=a/b=\alpha/\beta$. Or, $\alpha$ et $\beta$ sont premiers entre eux ([C1.III.2, remarque 6.12]), si bien que nous avons démontré la proposition suivante :

Proposition 1.6
Tout nombre rationnel $r$ peut s’écrire sous la forme $a/b$, avec $a$ et $b$ premiers entre eux.

La représentation d’un nombre rationnel $r$ sous la forme d’une fraction d’entiers relatifs premiers entre eux est donc un choix particulier parmi toutes les représentations possibles. On appelle une telle représentation, qui consiste en le couple $(a,b)\in\mathbb Z\times \mathbb Z^*$ tel que $r=a/b$, une forme irréductible de ce nombre.

Toutefois, il peut exister a priori plusieurs formes irréductibles d’un même nombre. Par exemple, le nombre $(-7/23)$ est représenté ici sous forme irréductible puisque $-7$ et $23$ sont premiers entre eux, donc le couple $(-7,23)$ est une telle forme.

Mais on peut aussi l’écrire $7/(-23)$, puisque $(-7).(-23)=7.23$, donc le couple $(7,-23)$ est une autre forme irréductible ! Ainsi, il existe au moins deux représentations irréductibles de ce nombre et en fait, il n’en existe jamais que deux.

Proposition 1.7
Si $r$ est un nombre rationnel non nul, alors il existe exactement deux formes irréductibles de $r$.

Démonstration
L’existence d’une telle forme a été établie précédemment : si $r=a/b$, en simplifiant $a$ et $b$ par leur p.g.c.d on obtient une représentation de $r$ sous forme irréductible. Or, si $(a,b)$ est une forme irréductible de $r$, le couple $(-a,-b)$ donne une autre forme irréductible de $r$ puisque $pgcd(-a,-b)=pgcd(a,b)=1$, si bien qu’il existe au moins deux telles formes, puisque de toute façon on a $b\neq -b$ (donc $(a,b)\neq (-a,-b)$).
Supposons maintenant que $a/b=c/d$, avec $pgcd(a,b)=pgcd(c,d)=1$. Par définition de $\mathbb Q$, on a donc $ad=bc$, et par le lemme de Gauss ([C1.III.2, théorème 5.7]), on a alors $a|c$ (puisque $a|bc$ et $pgcd(a,b)=1$) et $c|a$ (puisque $c|ad$ et $pgcd(c,d)=1$), de sorte que $a=\pm c$. De même, on a $b=\pm d$, si bien qu’on a soit $c/d=a/b$ (dans le cas où $a=c$), soit $c/d=(-a)/(-b)$ (dans le cas où $b=d$), et les deux formes irréductibles $(a,b)$ et $(-a,-b)$ sont donc les seules possibles. $\square$

Remarque 1.8
Nous n’avons défini stricto sensu le p.g.c.d de deux entiers relatifs que s’ils sont tous deux non nuls. Cependant, la définition s’étend naturellement au cas où l’un seulement est non nul, et permet ainsi d’inclure $0$ comme cas particulier de cette proposition : les formes irréductibles de $0$ sont $0/1$ et $0/(-1)$.

Définition 1.9
Si $r$ est un nombre rationnel, sa forme irréductible $(a,b)$ telle que $b>0$ sera appelée forme irréductible canonique de $r$.

L’existence d’une forme irréductible canonique signifie qu’on peut toujours choisir, dans l’écriture fractionnaire d’un nombre rationnel, le dénominateur comme un entier naturel.

1.3. Exercices

Exercice 1.1
i) Les nombres rationnels $\dfrac{110}{273}$ et $\dfrac{1431}{3529}$ sont-ils égaux ? Sinon, corriger le numérateur ou le dénominateur d’un des deux nombres pour obtenir deux fractions égales.
ii) Mettre sous forme irréductible canonique les nombres $\dfrac{30}{-105}$, $\dfrac{-231}{182}$ et $\dfrac{378}{1980}$.
iii) En utilisant des décompositions en nombres premiers, multiplier $-42/65$ par $286/231$.

2.Extension de la structure arithmétique de l’ensemble $\mathbb Z$

Après avoir décrit de manière axiomatique la multiplication de l’ensemble $\mathbb Q$ de manière à déterminer celui-ci de manière univoque, nous procédons maintenant à l’extension du reste de la structure arithmétique (pure) de l’ensemble $\mathbb Z$ à l’ensemble $\mathbb Q$, en définissant l’addition, la division et la soustraction de nombres rationnels.

2.1. Réduction au même dénominateur

4. Décomposition multiplicative et valuations $p$-adiques

Dans cette section et jusqu’à la fin du chapitre, nous abordons l’extension de propriétés arithmétiques de l’ensemble $\mathbb Z$ à l’ensemble $\mathbb Q$. Mais puisque en axiomatisant cet ensemble, nous avons ajouté des inverses multiplicatifs à tout élément non nul, par la proposition 2.9 tout nombre rationnel $q$ est divisible par tout nombre rationnel non nul $r$ ! Cela signifie que la relation de divisibilité ne présente plus aucun intérêt arithmétique dans l’ensemble $\mathbb Q$, or nous avons défini l’arithmétique dans $\mathbb N$ et dans $\mathbb Z$ comme l’étude de cette relation…

En fait, l’existence des décompositions en nombres premiers subsiste de manière essentielle dans la théorie des nombres rationnels, et on l’étudie en rapport à des « raffinements » associés à chaque nombre premier et obtenus à partir de l’extension de la notion d’exposant évoquée à la section [C1.III.2 :: Nombres primaires], laquelle nécessite de définir auparavant les puissances négatives d’un nombre rationnel.

1.1. Puissances des nombres rationnels

Dans la section [C1.III.2 :: Puissances des entiers relatifs], nous avons défini proprement la puissance d’un nombre entier relatif par un entier naturel quelconque. Nous allons définir ici la puissance d’un nombre rationnel par un entier relatif.

Définition 4.1
Soit $r$ un nombre rationnel.
A) Si $n$ est un nombre entier naturel, on définit le nombre rationnel $r$ (à la) puissance $n$, noté $r^n$, par récurrence, de la manière suivante :
i) Si $n=0$, on pose $r^0=1$
ii) On pose $r^{n+1}:=r^n.r$, en supposant que $r^n$ est défini
B) Si $r$ est non nul et $n$ est un nombre entier négatif, on définit le nombre rationnel $r^n$ comme $1/r^{-n}$.

La définition de la puissance d’un nombre rationnel par un entier naturel est exactement la même que celle de la puissance d’un nombre entier relatif : elle prolonge donc celle-ci et c’est celle que nous adopterons aussi pour les nombres réels et les nombres complexes.

L’extension de la définition consiste principalement à définir les puissances négatives à partir de l’inversion. Cette définition est justifiée dans la mesure où pour tout nombre rationnel $r\neq 0$ et tout entier $n\leq 0$, l’entier $-n$ est positif, et le nombre rationnel $r^{-n}$ est donc bien défini par récurrence et différent de zéro.

Il faut prendre garde toutefois que la puissance n’est pas toujours définie pour $r=0$, puisque $0^1=0$, et donc que $0^{-1}$ n’a pas de sens. C’est en fait le seul cas où $r^n$ ne peut pas être défini pour $n<0$.

Les propriétés des puissances entières des nombres rationnels sont essentiellement les mêmes que dans le cas des nombres entiers (évoquées dans [C1.III.2, proposition 5.2]) :

Proposition 4.2
Soient $q$ et $r$ des nombres rationnels, et $m,n$ des entiers relatifs. Lorsque les puissances sont toutes définies, on a :
i) $(q.r)^{m}=q^m.r^m$
ii) $q^{m+n}=q^m.q^n$
iii) $(q^m)^n=q^{m.n}$.

Démonstration
Lorsque $m,n\geq 0$, les puissances sont toujours définies et les démonstrations sont identiques à celles de la démonstration de [C1.III.2, proposition 5.2] (op. cit.) : nous ne les reproduisons pas ici. On traite donc du cas où l’un des nombres $m$ et $n$ est strictement négatif, et par symétrie on peut choisir $m<0$.
i) On a $(q.r)^m=1/(q.r)^{-m}$ (par définition) $=1/(q^{-m}.r^{-m})$ (par le cas $m>0$) $=(1/q^{-m}).(1/r^{-m})=q^m.r^m$ (par définition).
ii) On distingue deux cas, selon que $m+n\geq 0$ ou que $m+n<0$. Supposons que $m+n\geq 0$, posons $k=m+n$ et raisonnons par récurrence sur $k$. Si $k=0$, on a $m=-n$, et $q^{m+n}=q^k=q^0=1=(q^m).(1/q^m)=q^m.q^{-m}=q^m.q^n$ et la propriété est vérifiée. Supposons qu’elle le soit au rang $k$, et que $m+n=k+1$ : comme $m<0$, on a $n>0$, donc on peut écrire $n$ sous la forme $n=l+1$, d’où $m+l=k$, et on a alors $q^{m+n}=q^{k+1}=q^{m+l+1}=q^{m+l}.q$ (par définition) $=(q^m.q^l).q$ (par hypothèse de récurrence appliquée à $m+l=k$) $=q^m.q^{l+1}=q^m.q^n$, et la propriété est vérifiée au rang $k+1$. Par récurrence, elle l’est pour tout $k\in\mathbb N$, donc pour tous $m,n$ tels que $m<0$ et $m+n\geq 0$.
Supposons maintenant que $m+n<0$, et distinguons à nouveau deux cas, selon que $n\leq 0$ ou $n> 0$. Si $n\leq 0$, on a $q^{m+n}=1/q^{-m-n}$ (par définition) $=1/(q^{-m}.q^{-n})$ (par le cas $m,n\geq 0$) $=(1/q^{-m}).(1/q^{-n})=q^m.q^n$. Si $n>0$, on a $-n<0$ et : comme $-m-n>0$, par le cas $m+n\geq 0$ et en échangeant les rôles de $n$ et de $-m$, on obtient également $q^{m+n}=1/q^{-m-n}=1/(q^{-m}.q^{-n})=(1/q^{-m}).(1/q^{-n})=q^m.q^n$.
iii) On a $(q^m)^n=(1/q^{-m})^n$ (par définition d’une puissance négative) $=(1/q)^{-mn}$ (par le cas $m,n\geq 0$) $=q^{mn}$. $\square$

Notons que par définition, si $r$ est un nombre rationnel non nul, on a $r^{-1}=1/r$, et donc pour tout entier naturel $n$, $(1/r)^n=(r^{-1})^n=r^{-n}=1/r^n$ par la proposition 4.2.

4.2. Valuations $p$-adiques

La factorisation des entiers naturels (et donc des entiers relatifs) en produit de puissances de nombres premiers par le théorème de Gauss ([C1.III.2, théorème 5.2]) peut dans un certain sens s’étendre aux nombres rationnels.

Il existe au moins deux façons de le faire : nous commençons par exposer la plus simple, qui consiste à décomposer le numérateur $a$ et le dénominateur $b$ d’une représentation $a/b$ d’un nombre rationnel en nombres premiers $p_1,\ldots,p_n$, et à réécrire la fraction $a/b$ sous la forme d’un produit de ces facteurs premiers, avec des puissances positives ou négatives.

En sélectionnant un des nombres premiers $p_i$ de cette décomposition « multiplicative », nous pouvons alors considérer le nombre $a/b$ « relativement au nombre $p_i$ », ce qui permet d’en tirer des informations arithmétiques intéressantes. Or, si $p\in\mathbb N$ est un nombre premier, nous avons défini dans la section [Arithmétique des entiers relatifs :: Nombres primaires] (op. cit.) l’exposant de $p$ dans un entier relatif non nul. Nous pouvons utilement étendre cette notion à tout nombre rationnel non nul de la manière suivante :

Définition 4.3
Si $r=a/b$ est un nombre rationnel non nul, la valuation $p$-adique de $r$ est le nombre entier relatif $v_p(r)=v_p(a)-v_p(b)$, où $v_p(a)$ est l’exposant de $p$ dans $a$.

Remarque 4.4
La valuation ne peut être définie que pour un nombre rationnel non nul, puisque si $a=0$, l’exposant de $p$ dans $a$ n’est pas défini.

A priori, la valuation $p$-adique pourrait dépendre du choix d’une représentation d’un rationnel non nul.

Pour montrer qu’elle ne dépend pas d’un tel choix et qu’elle est donc bien définie, supposons que $r=a/b=c/d$ : on a $ad=bc$ dans $\mathbb Z$, donc par [C1.III.2, proposition 6.7], $v_p(a)+v_p(d)=v_p(ad)=v_p(bc)=v_p(b)+v_p(c)$, si bien que $v_p(a)-v_p(b)=v_p(c)-v_p(d)$, et $v_p(r)$ est bien définie.

Aussi, notons que si $n\in\mathbb Z$, on a $v_p(n/1)=v_p(n)-v_p(1)=v_p(n)$ pour tout entier naturel premier $p$, puisque $p$ ne divise pas $1$, si bien que la valuation $p$-adique d’un entier non nul $n$ vu comme le nombre rationnel $1/n$ est l’exposant de $p$ dans $n$ : les valuations $p$-adiques sont les prolongements des exposants de $\mathbb Z^*$ à $\mathbb Q^*$.

Tout comme l’exposant « transforme » la multiplication des entiers relatifs non nuls en l’addition des entiers naturels, la valuation « transforme » la multiplication des rationnels non nuls en l’addition des entiers relatifs.

Cette propriété est regroupée avec les propriétés élémentaires des valuations $p$-adiques dans la proposition suivante. Toutes ces propriétés sont analogues de celles de la valeur absolue (section 3.2), pour des raisons profondes qui dépassent le cadre de ce cours.

Proposition 4.5
Pour tous nombres rationnels non nuls $r$ et $s$, on a :
i) $v_p(1)=0$
ii) $v_p(r.s)=v_p(r)+v_p(s)$
iii) $v_p(r+s)\geq \min\{v_p(r),v_p(s)\}$.

Démonstration
i) On a $v_p(1)=v_p(1/1)=v_p(1)-v_p(1)=0$.
ii) Ecrivons $r=a/b$ et $s=c/d$ : on a $v_p(r.s)=v_p(ac/bd)=v_p(ac)-v_p(bd)$ (par définition) $=v_p(a)+v_p(c)-v_p(b)-v_p(d)$ (par [C1.III.2 proposition 6.7], op. cit.) $=(v_p(a)-v_p(b))+(v_p(c)-v_p(d))=v_p(r)+v_p(s)$.
iii) Avec les mêmes notations, nous voulons montrer que $v_p(ad+bc)-v_p(bd)\geq \min\{v_p(a)-v_p(b),v_p(c)-v_p(d)\}$. En réécrivant $v_p(bd)=v_p(b)+v_p(d)$, distinguons deux cas, selon la valeur du minimum $m:=\min\{v_p(a)-v_p(b),v_p(c)-v_p(d)\}$ au membre de droite de l’inégalité à démontrer. Si $m=v_p(a)-v_p(b)$, nous voulons montrer que $v_p(ad+bc)-v_p(b)-v_p(d)\geq v_p(a)-v_p(b)$, ou encore en ajoutant $v_p(b)+v_p(d)$ aux deux membres, que $v_p(ad+bc)\geq v_p(a)+v_p(d)=v_p(ad)$. Or, par définition on a $p^{v_p(ad)}|ad$ et comme $v_p(a)-v_p(b)\leq v_p(c)-v_p(d)$, on a $v_p(ad)=v_p(a)+v_p(d)\leq v_p(c)+v_p(b)=v_p(bc)$, d’où aussi $p^ {v_p(ad)}|bc$, si bien que finalement, on a $p^{v_p(ad)}|ad+bc$, d’où $v_p(ad+bc)\geq v_p(a)+v_p(d)$, par définition de l’exposant de $p$ dans $ad+bc$. Si $m=v_p(c)-v_p(d)$, on raisonne exactement de la même manière en échangeant les rôles de $(a,b)$ et de $(c,d)$. $\square$

La valuation $p$-adique d’un nombre rationnel non nul est toujours un entier relatif. Grâce à cette notion, on peut établir la décomposition multiplicative d’un nombre rationnel strictement positif comme généralisation de la décomposition d’un entier naturel en nombres premiers.

Lemme 4.6
Soient $r$ un nombre rationnel strictement positif, et $(a,b)$ sa forme irréductible canonique. Si $p$ est un entier naturel premier, alors :
i) On a $v_p(r)=0$ si et seulement $p$ ne divise ni $a$, ni $b$
ii) On a $v_p(r)>0$ si et seulement si $p|a$ mais $p\nmid b$, et alors $v_p(r)=v_p(a)$
iii) On a $v_p(r)<0$ si et seulement si $p|b$ mais $p\nmid a$, et alors $v_p(r)=-v_p(b)$.

Démonstration
i) Par définition, on a $v_p(r)=v_p(a)-v_p(b)$, donc si $v_p(r)=0$, on a $v_p(a)=v_p(b)$ : si $v_p(a)>0$, alors $p|a$ et $p|b$, ce qui contredit la primalité relative de $a$ et $b$, d’où $p\nmid a$ et $p\nmid b$. Inversement, si $p$ ne divise ni $a$, ni $b$, on a $v_p(r)=v_p(a)-v_p(b)=0-0=0$.
ii) Supposons que $v_p(r)>0$ : si $b|p$, on a $v_p(a)>v_p(b)>0$, donc $p|a$ également, ce qui est impossible à nouveau puisque $pgcd(a,b)=1$. On en déduit que $p\nmid b$, $v_p(b)=0$, et $v_p(r)=v_p(a)-v_p(b)=v_p(a)$.
Inversement, si $p|a$ on ne peut avoir $p|b$ par primalité relative, donc on a $v_p(r)=v_p(a)>0$.
iii) Supposons que $v_p(r)<0$ : si $a|p$, on a $v_p(b)>v_p(a)>0$, donc $p|b$ également, ce qui est impossible, d’où $p\nmid a$, $v_p(a)=0$, et $v_p(r)=v_p(a)-v_p(b)=-v_p(b)$. La réciproque se démontre de manière évidente. $\square$

Dans le théorème suivant, qui prolonge le théorème de Gauss ([C1.III.2, théorème 5.10], op. cit.), nous utilisons une notation nouvelle pour le produit d’un nombre fini de nombres rationnels. La notation est analogue à celle des sommes finies (section [C1.III.2 :: Critères de divisibilité]), sauf qu’on ajoute à l’indexation (ici $i$ variant de $1$ à $n$) une condition sur les indices (ici $v_{p_i}(r)>0$ ou $v_{p_i}(r)<0$). Ceci signifie qu’on effectue le produit des nombres indexés par $i$, en ne retenant que ceux pour lesquels la condition sur l’indice $i$ est vérifiée. En toute rigueur nous devrions définir intégralement le procédé, ce que nous ferons plutôt dans un cours ultérieur : la notation est ici suffisamment claire.

Théorème 4.7
Si $r$ est un nombre rationnel strictement positif, il existe un entier naturel $n$ et des nombres premiers $p_1<\ldots <p_n$ uniques, ainsi que des entiers relatifs non nuls $k_1,\ldots,k_n$ uniques, tels que $r=p_1^{k_1}\ldots p_n^{k_n}$. De plus, les nombres $k_i$ sont les $v_{p_i}(r)$.

Démonstration
Si $r=1$, alors $n=0$ convient : la décomposition est « vide ».
Si $r\neq 1$, écrivons $r=a/b$ sous forme irréductible canonique, c’est-à-dire avec $b>0$ et $a$ et $b$ premiers entre eux, de sorte que $a\neq b$. Soient $n\in\mathbb N$ et $p_1<\ldots <p_n$ les nombres premiers apparaissant avec un exposant non nul soit dans la décomposition de $a$ en nombres premiers, soit dans celle de $b$. Par le lemme 4.6, pour tout $i=1,\ldots,n$ on a $v_{p_i}(r)\neq 0$, et $a=\prod_{i,v_{p_i}>0} p_i^{v_{p_i}(r)}$ et $b=\prod_{i,v_{p_i}(r)<0} p_i^{-v_{p_i}(r)}$, d’où $r=a/b=\prod_i p_i^{v_{p_i}(r)}$, et l’existence de la décomposition est démontrée.
Concernant l’unicité de la décomposition, supposons que $r=p_1^{k_1}\ldots p_n^{k_n}$ avec $p_1<\ldots <p_n$ des entiers naturels premiers et $k_i\in\mathbb Z^*$ pour tout $i=1,\ldots,n$, et soit à nouveau $(a,b)$ la forme irréductible canonique de $r$. Par le lemme 4.6, les nombres premiers $p_i$, $i=1,\ldots,n$, sont les facteurs premiers de $a$ ou de $b$, et pour tout $i=1,\ldots,n$ on a $k_i=v_{p_i}(r)$, si bien que la décomposition est unique. $\square$

Exemple 4.8
Décomposons le nombre rationnel $r=6375/1485$ en nombres premiers. Le numérateur et le dénominateur sont divisibles par $5$, on peut donc simplifier en $r=1275/297$. Deux décompositions en nombres premiers donnent $1275=3.5^2.17$ et $297=3^3.11$, donc la décomposition cherchée est $r=3^{-2}.5.11^{-1}.17$.

La figure suivante propose une interprétation graphique de la décomposition d’un nombre rationnel positif en puissances de nombres premiers.

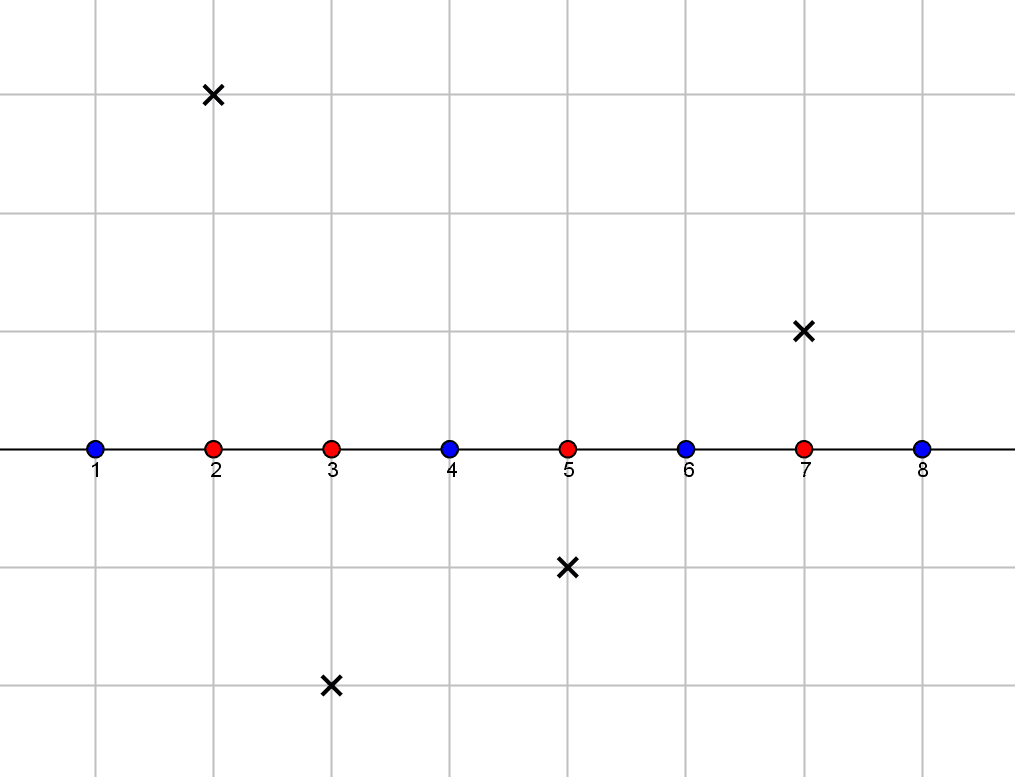
Grâce à la notion de valuation, on peut aussi redémontrer de manière élémentaire que le nombre réel $\sqrt 2$ n’est pas rationnel :

Proposition 4.9
Il n’existe aucun nombre rationnel $r$ tel que $r^2=2$.

Démonstration
Supposons par l’absurde qu’il existe $r\in\mathbb Q$, nécessairement non nul, tel que $r^2=2$. On considère alors la valuation $2$-adique de $2$, qui vaut $1$ puisque $1$ est l’exposant de $2$ dans $2$. Par la proposition 4.5, on peut aussi écrire $v_2(r^2)=v_2(r.r)=v_2(r)+v_2(r)=2v_2(r)$. Il s’ensuit que $1=2v_2(r)$, soit $v_2(r)=\frac{1}{2}$, ce qui est impossible puisque la valuation $2$-adique est toujours un entier relatif. Par reductio ad absurdum, on en déduit qu’il n’existe pas de racine carrée de $2$ dans l’ensemble $\mathbb Q$. $\square$

L’élément déterminant dans la démonstration de la proposition 4.9 est le caractère impair de l’exposant de $2$ (sa valuation $2$-adique comme nombre rationnel) dans le nombre entier $2$. Cette idée permet en fait de caractériser tous les nombres rationnels qui possèdent une racine carrée dans $\mathbb Q$.

Théorème 4.10
Un nombre rationnel $r$ possède une racine carrée dans $\mathbb Q$ si et seulement si il est positif et pour tout entier naturel premier $p$, l’entier relatif $v_p(r)$ est pair.

Démonstration
Si $r<0$, alors comme le carré d’un nombre rationnel est toujours positif par [Axiomes et structure de l’ensemble $\mathbb Q$, proposition 3.2], $r$ ne peut avoir de racine carrée; par contraposée un nombre rationnel possédant une racine carrée est toujours positif.
Si $r=0$, on a $r=0^2$, donc $r$ possède une racine carrée. Supposons désormais que $r> 0$ et décomposons $r$ en facteurs premiers sous la forme $p_1^{v_{p_1}(r)}\ldots p_n^{v_{p_n}(r)}$ par le théorème 4.7. Si pour tout entier naturel premier $p$, l’entier $v_p(r)$ est pair, en particulier pour $i=1,\ldots,n$ $v_{p_i}(r)$ est pair, on peut l’écrire sous la forme $v_{p_i}(r)=2k_i$, $k_i\in\mathbb Z$. Le nombre rationnel $q=p_1^{k_1}\ldots p_n^{k_n}$ est alors une racine carrée de $r$, puisque $q^2=p_1^{2k_1}\ldots p_n^{2k_n}=r$.
Réciproquement, si $r$ possède une racine carrée rationnelle $s$, on peut supposer que $s>0$ (car si $s<0$, on a $-s>0$ et $(-s)^2=s^2=r$, donc on peut toujours en tirer une racine carrée positive). Décomposons $s$ en facteurs premiers sous la forme $q_1^{l_1}\ldots q_m^{l_m}$, avec $q_1<\ldots <q_m$ et $v_{q_j}(s)=l_j\in\mathbb Z^\times$ pour tout $j$ : on a $s^2=q_1^{2l_1}\ldots q_m^{2l_m}=r$, donc par unicité de la décomposition de $r$ (théorème \ref{DECOMPQ}) on a $\{q_1,\ldots,q_m\}=\{p_1,\ldots,p_n\}$ et la valuation $p_i$-adique $v_{p_i}(r)=2l_i$ de $r$ est paire pour tout $i=1,\ldots,n$. Puisque la valuation $p$-adique de $r$ est nulle pour tous les autres entiers naturels premiers $p$ par le lemme 1, elle est paire pour tous les nombres premiers. $\square$

4.4. Exercices

Exercice 4.11
i) Démontrer par récurrence que pour tout entier naturel premier $p$, pour tout nombre rationnel non nul $r$ et pour tout entier naturel $m$, on a $v_p(r^m)=m.v_p(r)$. En déduire que pour tout entier naturel premier $p$ et pour tout entier naturel $m>1$, $p$ n’a pas de racine $m$-ième dans $\mathbb Q$ (c’est-à-dire qu’il n’existe pas de nombre rationnel $r$ tel que $r^m=p$).
ii) Soit $r$ un nombre rationnel non nul. Montrer que $v_p(r)=v_p(|r|)$ pour tout entier naturel premier $p$.
iii) Démontrer la réciproque de la clause (iii) du lemme 4.6.

Problème 4.12
L’objectif de ce problème est de généraliser le théorème 4.10 sous la forme suivante : si $m$ est un entier naturel $>1$ et $r$ un rationnel non nul, alors $r$ possède une racine $m$-ième dans $\mathbb Q$ (c’est-à-dire : il existe un rationnel $s$ tel que $s^m=r$) si et seulement si on se trouve dans l’un des deux cas (mutuellement exclusifs) suivants :
– $m$ est pair, $r>0$ et $m|v_p(r)$ pour tout nombre premier $p$
– $m$ est impair et $m|v_p(r)$ pour tout nombre premier $p$.
A) On suppose d’abord que $m$ est pair.
i) Montrer que si $r<0$, $r$ ne possède pas de racine $m$-ième dans $\mathbb Q$.
ii) Montrer que si $r>0$, alors $r$ possède une racine $m$-ième dans $\mathbb Q$ si et seulement si $m|v_p(r)$ pour tout nombre premier $p$.
B) On suppose désormais que $m$ est impair.
iii) Montrer que si $r\neq 0$ et $m|v_p(r)$ pour tout nombre premier $p$, et si $p_1^{k_1}\ldots p_n^{k_n}$ est la décomposition de $|r|$ en facteurs premiers, alors pour $s:=p_1^{k_1/m}\ldots m_n^{k_1/m}$, on a $(|r|/r)^m.s^m=r$.
iv) Montrer que si $r\neq 0$ et $r$ possède une racine $m$-ième $s$ dans $\mathbb Q$, alors $m|v_p(r)$ pour tout nombre premier $p$.
C) Conclure, sans oublier de traiter le cas où $r=0$.

5. Commensurabilité